Informationstheorie/Anwendung auf die Digitalsignalübertragung

1. Informationstheorie
2. Information zwischen zwei wertdiskreten Zufallsgrößen
3. Anwendung auf die Digitalsignalübertragung

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Informationstheoretisches Modell der Digitalsignalübertragung

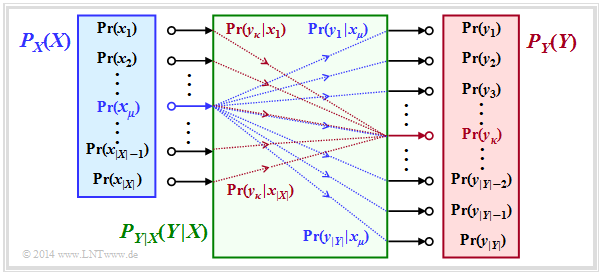
Die bisher allgemein definierten Entropien werden nun auf die Digitalsignalübertragung angewendet, wobei wir von einem digitalen Kanalmodell ohne Gedächtnis (englisch: Discrete Memoryless Channel, DMC) entsprechend der nachfolgenden Grafik ausgehen:

• Die Menge der möglichen Quellensymbole wird durch die diskrete Zufallsgröße $X$ charakterisiert, wobei $|X|$ den Quellensymbolumfang angibt:

$$X = \{\hspace{0.05cm}x_1\hspace{0.05cm}, \hspace{0.05cm} x_2\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.1cm} ,\hspace{0.05cm} x_{\mu}\hspace{0.05cm}, \hspace{0.05cm}...\hspace{0.1cm} , \hspace{0.05cm} x_{|X|}\hspace{0.05cm}\}\hspace{0.05cm}.$$

• Entsprechend kennzeichnet $Y$ die Menge der Sinkensymbole mit dem Symbolvorrat $|Y|$:

$$Y = \{\hspace{0.05cm}y_1\hspace{0.05cm}, \hspace{0.05cm} y_2\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.1cm} ,\hspace{0.05cm} y_{\kappa}\hspace{0.05cm}, \hspace{0.05cm}...\hspace{0.1cm} , \hspace{0.05cm} Y_{|Y|}\hspace{0.05cm}\}\hspace{0.05cm}.$$

• Meist gilt $|Y|$ = $|X|$. Möglich ist aber auch $|Y|$ > $|X|$, zum Beispiel beim Binary Erasure Channel (BEC) mit $X$ = {0, 1} und $Y$ = {0, 1, E} ⇒ $|X|$ = 2, $|Y|$ = 3.
• Das Sinkensymbol $E$ kennzeichnet eine Auslöschung (englisch: Erasure). Das Ereignis $Y$ = $E$ gibt an, dass eine Entscheidung für 0 oder für 1 zu unsicher wäre.
• Die Symbolwahrscheinlichkeiten der Quelle und der Sinke sind in der oberen Grafik durch die Wahrscheinlichkeitsfunktionen $P_X(X)$ und $P_Y(Y)$ berücksichtigt, wobei gilt:

$$P_X(x_{\mu}) = {\rm Pr}( X = x_{\mu})\hspace{0.05cm}, \hspace{0.3cm} P_Y(y_{\kappa}) = {\rm Pr}( Y = y_{\kappa})\hspace{0.05cm}.$$

• Es gelte: $P_X(X)$ und $P_Y(Y)$ enthalten keine Nullen ⇒ $\text{supp}(P_X)$ = $P_X$, $\text{supp}(P_Y)$ = $P_Y$. Diese Voraussetzung erleichtert die Modellbeschreibung, ohne Verlust an Allgemeingültigkeit.
• Alle Übergangswahrscheinlichkeiten des digitalen gedächtnislosen Kanals (DMC) werden durch die bedingte Wahrscheinlichkeitsfunktion $P_{Y|X}(Y|X)$ erfasst. Mit $x_μ ∈ X$ und $y_κ ∈ Y$ gelte hierfür folgende Definition:

$$P_{Y\hspace{0.01cm}|\hspace{0.01cm}X}(y_{\kappa}\hspace{0.01cm} |\hspace{0.01cm} x_{\mu}) = {\rm Pr}(Y\hspace{-0.1cm} = y_{\kappa}\hspace{0.03cm} | \hspace{0.03cm}X \hspace{-0.1cm}= x_{\mu})\hspace{0.05cm}.$$

In obiger Grafik ist $P_{Y|X}(⋅)$ als ein Block mit $|X|$ Eingängen und $|Y|$ Ausgängen dargestellt. Die blauen Verbindungen markieren die Übergangswahrscheinlichkeiten $\text{Pr}(y_i | x_μ)$ ausgehend von $x_μ$ mit 1 ≤ $i$ ≤ $|Y|$, während alle roten Verbindungen bei $y_κ$ enden: $\text{Pr}(y_κ | x_i)$ mit 1 ≤ $i$ ≤ $|X|$.

Bevor wir die Entropien für die einzelnen Wahrscheinlichkeitsfunktionen angeben, nämlich $P_X(X) ⇒ H(X)$, $P_Y(Y) ⇒ H(Y)$, $P_{XY}(X) ⇒ H(XY)$, $P_Y|X(Y|X) ⇒ H(Y|X)$, $P_{X|Y}(X|Y) ⇒ H(X|Y)$, sollen die Aussagen der letzten Seite an einem Beispiel verdeutlicht werden.

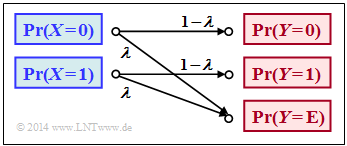Im Buch Kanalcodierung behandeln wir den Binary Erasure Channel (BEC), der rechts in etwas modifizierter Form skizziert ist.

Dabei gelten folgende Voraussetzungen:

• Das Eingangsalphabet ist binär: $X$ = (0, 1) ⇒ $|X|$ = 2, während am Ausgang drei Werte möglich sind: $Y$ = (0, 1, $E$) ⇒ $|Y|$ = 3.
• „E” kennzeichnet den Fall, dass sich der Empfänger aufgrund von zu großen Kanalstörungen nicht für eines der Binärsymbole 0 oder 1 entscheiden kann. „E” steht hierbei für Erasure (Auslöschung).
• Beim BEC gemäß obiger Skizze werden sowohl eine gesendete „0” als auch eine „1” mit der Wahrscheinlichkeit $λ$ ausgelöscht, während die Wahrscheinlichkeit einer richtigen Übertragung jeweils 1 – $λ$ beträgt.
• Dagegen werden Übertragungsfehler durch das BEC–Modell ausgeschlossen ⇒ die bedingten Wahrscheinlichkeiten Pr( $Y$ = 1 | $X$ = 0 ) sowie Pr( $Y$ = 0 | $X$ = 1) sind jeweils 0.

Beim Sender seien die Nullen und Einsen nicht unbedingt gleichwahrscheinlich. Vielmehr verwenden wir die beiden Wahrscheinlichkeitsfunktionen

$$\begin{align*}P_X(X) \hspace{-0.15cm} & = \hspace{-0.15cm} \big ( {\rm Pr}( X = 0)\hspace{0.05cm}, {\rm Pr}( X = 1) \big )\hspace{0.05cm},\\ P_Y(Y) \hspace{-0.15cm} & = \hspace{-0.15cm} \big ( {\rm Pr}( Y = 0)\hspace{0.05cm}, {\rm Pr}( Y = 1)\hspace{0.05cm}, {\rm Pr}( Y = {\rm E}) \big )\hspace{0.05cm}.\end{align*}$$

Aus obigem Modell erhalten wir dann:

$$\begin{align*}P_Y(0) \hspace{-0.15cm} & = \hspace{-0.15cm} {\rm Pr}( Y \hspace{-0.1cm} = 0) = P_X(0) \cdot ( 1 - \lambda)\hspace{0.05cm}, \\ P_Y(1) \hspace{-0.15cm} & = \hspace{-0.15cm} {\rm Pr}( Y \hspace{-0.1cm} = 1) = P_X(1) \cdot ( 1 - \lambda)\hspace{0.05cm}, \\ P_Y({\rm E}) \hspace{-0.15cm} & = \hspace{-0.15cm} {\rm Pr}( Y \hspace{-0.1cm} = {\rm E}) = P_X(0) \cdot \lambda \hspace{0.1cm}+\hspace{0.1cm} P_X(1) \cdot \lambda \hspace{0.05cm}.\end{align*}$$

Fassen wir nun $P_X(X)$ und $P_Y(Y)$ als Vektoren auf, so lässt sich das Ergebnis wie folgt darstellen:

$$P_{\hspace{0.05cm}Y}(Y) = P_X(X) \cdot P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{-0.01cm} X) \hspace{0.05cm},$$

wobei die Übergangswahrscheinlichkeiten $\text{Pr}(y_κ | x_μ)$ durch folgende Matrix berücksichtigt sind:

$$P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{-0.01cm} X) = \begin{pmatrix} 1 - \lambda 0 \lambda\\ 0 1 - \lambda \lambda \end{pmatrix}\hspace{0.05cm}.$$

Beachten Sie: Wir haben diese Darstellung nur gewählt, um die Beschreibung zu vereinfachen. $P_X(X)$ und $P_Y(Y)$ sind keine Vektoren im eigentlichen Sinne und $P_{Y|X}(Y|X)$ ist keine Matrix.

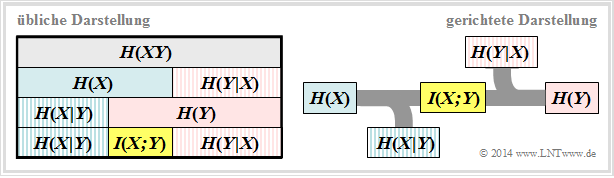
Alle in Kapitel 3.2 definierten Entropien gelten auch für die Digitalsignalübertragung. Es ist aber zweckmäßig, anstelle des bisher verwendeten Schaubildes (linke Grafik) die rechte Darstellung zu wählen, bei der die Richtung von der Quelle $X$ zur Sinke $Y$ erkennbar ist.

Interpretieren wir nun ausgehend vom allgemeinen DMC–Kanalmodell die rechte Grafik:

• Die Quellenentropie (englisch: Source Entropy) $H(X)$ bezeichnet den mittleren Informationsgehalt der Quellensymbolfolge. Mit dem Symbolumfang $|X|$ gilt:

$$H(X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(X)}\right ] \hspace{0.1cm} = -{\rm E} \left [ {\rm log}_2 \hspace{0.1cm}{P_X(X)}\right ] \hspace{0.2cm} =\hspace{0.2cm} \sum_{\mu = 1}^{|X|} P_X(x_{\mu}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(x_{\mu})} \hspace{0.05cm}.$$

• Die Äquivokation (auch Rückschlussentropie genannt, englisch: Equivocation) $H(X|Y)$ gibt den mittleren Informationsgehalt an, den ein Betrachter, der über die Sinke $Y$ genau Bescheid weiß, durch Beobachtung der Quelle $X$ gewinnt:

$$H(X|Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{-0.01cm}Y}(X\hspace{-0.01cm} |\hspace{0.03cm} Y)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{0.03cm}Y} (\hspace{0.05cm}x_{\mu}\hspace{0.03cm} |\hspace{0.05cm} y_{\kappa})} \hspace{0.05cm}.$$

• Die Äquivokation ist der Anteil der Quellenentropie $H(X)$, der durch Kanalstörungen (bei digitalem Kanal: Übertragungsfehler) verloren geht. Es verbleibt die Transinformation (englisch: Mutual Information) $I(X; Y)$, die zur Sinke gelangt:

$$I(X;Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)}{P_X(X) \cdot P_Y(Y)}\right ] \hspace{0.2cm} = H(X) - H(X|Y) \hspace{0.05cm}.$$

• Die Irrelevanz (manchmal auch Streuentropie genannt, englisch: Irrelevance) $H(Y|X)$ gibt den mittleren Informationsgehalt an, den ein Betrachter, der über die Quelle $X$ genau Bescheid weiß, durch Beobachtung der Sinke $Y$ gewinnt:

$$H(Y|X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{0.03cm} X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.03cm}X} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu})} \hspace{0.05cm}.$$

• Die Sinkenentropie $H(Y)$, der mittlere Informationsgehalt der Sinke, ist die Summe aus der nützlichen Transinformation $I(X; Y)$ und der Irrelevanz $H(Y|X)$, die ausschließlich von Kanalfehlern herrührt:

$$H(Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_Y(Y)}\right ] \hspace{0.1cm} = -{\rm E} \left [ {\rm log}_2 \hspace{0.1cm}{P_Y(Y)}\right ] \hspace{0.2cm} =I(X;Y) + H(Y|X) \hspace{0.05cm}.$$

Transinformationsberechnung für den Binärkanal

Die Definitionen der letzten Seite sollen nun an einem Beispiel verdeutlicht werden, wobei wir bewusst vermeiden, die Berechnungen durch die Ausnutzung von Symmetrien zu vereinfachen.

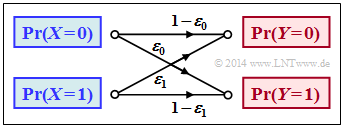Wir betrachten den allgemeinen Binärkanal (englisch: Binary Channel) ohne Gedächtnis gemäß der Skizze mit den Verfälschungswahrscheinlichkeiten.

$$\begin{align*}\varepsilon_0 \hspace{-0.15cm} & = \hspace{-0.15cm}{\rm Pr}(Y\hspace{-0.1cm} = 1\hspace{0.05cm} | X \hspace{-0.1cm}= 0) = 0.01\hspace{0.05cm},\\ \varepsilon_1 \hspace{-0.15cm} & = \hspace{-0.15cm} {\rm Pr}(Y\hspace{-0.1cm} = 0\hspace{0.05cm} | X \hspace{-0.1cm}= 1) = 0.2\hspace{0.05cm}\end{align*}$$

$$\Rightarrow \hspace{0.3cm} P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{-0.01cm} X) = \begin{pmatrix} 1 - \varepsilon_0 & \varepsilon_0\\ \varepsilon_1 & 1 - \varepsilon_1 \end{pmatrix} = \begin{pmatrix} 0.99 & 0.01\\ 0.2 & 0.8 \end{pmatrix} \hspace{0.05cm}.$$

Außerdem gehen wir von nicht gleichwahrscheinlichen Quellensymbolen aus:

$$P_X(X) = \big ( p_0, p_1 \big )= \big ( 0.1, 0.9 \big ) \hspace{0.05cm}.$$

Mit der binären Entropiefunktion erhält man so für die Quellenentropie:

$$H(X) = H_{\rm bin} (0.1) = 0.4690 \,{\rm bit} \hspace{0.05cm}.$$

Für die Wahrscheinlichkeitsfunktion der Sinke sowie für die Sinkenentropie ergibt sich somit:

$$P_Y(Y) = \big ( {\rm Pr}( Y\hspace{-0.1cm} = 0)\hspace{0.05cm}, {\rm Pr}( Y \hspace{-0.1cm}= 1) \big ) = \big ( p_0\hspace{0.05cm}, p_1 \big ) \cdot \begin{pmatrix} 1 - \varepsilon_0 & \varepsilon_0\\ \varepsilon_1 & 1 - \varepsilon_1 \end{pmatrix} $$

$$\begin{align*}\Rightarrow \hspace{0.3cm} {\rm Pr}( Y \hspace{-0.1cm}= 0)\hspace{-0.15cm} & = \hspace{-0.15cm} p_0 \cdot (1 - \varepsilon_0) + p_1 \cdot \varepsilon_1 = 0.1 \cdot 0.99 + 0.9 \cdot 0.2 = 0.279\hspace{0.05cm},\\ {\rm Pr}( Y \hspace{-0.1cm}= 1)\hspace{-0.15cm} & = \hspace{-0.15cm} 1 - {\rm Pr}( Y \hspace{-0.1cm}= 0) = 0.721\end{align*}$$

$$\Rightarrow \hspace{0.2cm} H(Y) = H_{\rm bin} (0.279) = 0.8541 \,{\rm bit} \hspace{0.05cm}. $$

Auf der nächsten Seite werden noch berechnet:

• die Verbundentropie $H(XY)$,
• die Transinformation $I(X; Y)$,
• die Rückschlussentropie $H(X|Y)$ ⇒ Äquivokation,
• die Streuentropie $H(Y|X)$ ⇒ Irrelevanz.

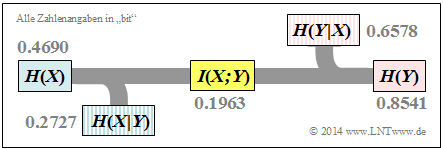
Diese Ergebnisse sind in der folgenden zusammenfassenden Grafik bereits mit aufgenommen.

Wir betrachten weiter den allgemeinen Binärkanal (englisch: Binary Channel) ohne Gedächtnis gemäß der Skizze, und es gelte weiterhin:

$$P_X(X) = \big ( p_0, p_1 \big )= \big ( 0.1, 0.9 \big ) \hspace{0.05cm},$$

$$\varepsilon_0 = {\rm Pr}(Y\hspace{-0.1cm} = 1\hspace{0.05cm} | X \hspace{-0.1cm}= 0) = 0.01\hspace{0.05cm}, \hspace{0.3cm} \varepsilon_1 ={\rm Pr}(Y\hspace{-0.1cm} = 0\hspace{0.05cm} | X \hspace{-0.1cm}= 1) = 0.2\hspace{0.05cm}.$$

Die Verbundwahrscheinlichkeiten $p_{\{μκ\}}$ = $\text{Pr}[(X = μ) ∩ (Y = κ)]$ zwischen Quelle und Sinke sind:

$$\begin{align*}p_{00}\hspace{-0.15cm} & = \hspace{-0.15cm} p_0 \cdot (1 - \varepsilon_0) = 0.099\hspace{0.05cm},\hspace{0.5cm}p_{01}= p_0 \cdot \varepsilon_0 = 0.001\hspace{0.05cm},\\ p_{10}\hspace{-0.15cm} & = \hspace{-0.15cm} p_1 \cdot (1 - \varepsilon_1) = 0.180\hspace{0.05cm},\hspace{0.5cm}p_{11}= p_1 \cdot \varepsilon_1 = 0.720\hspace{0.05cm}.\end{align*}$$

Daraus erhält man für

• die Verbundentropie (englisch Joint Entropy):

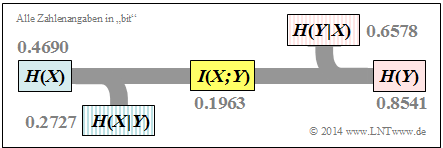
$$H(XY) = p_{00}\hspace{-0.05cm} \cdot \hspace{-0.05cm}{\rm log}_2 \hspace{0.05cm} \frac{1}{p_{00}} + p_{01} \hspace{-0.05cm} \cdot \hspace{-0.05cm}{\rm log}_2 \hspace{0.05cm} \frac{1}{p_{01}} + p_{10}\hspace{-0.05cm} \cdot \hspace{-0.05cm} {\rm log}_2 \hspace{0.05cm} \frac{1}{p_{10}} + p_{11} \hspace{-0.05cm} \cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.05cm} \frac{1}{p_{11}} = 1.1268\,{\rm bit} \hspace{0.05cm},$$

• die Transinformation (englisch Mutual Information):

$$I(X;Y) = H(X) + H(Y) - H(XY) = 0.4690 + 0.8541 - 1.1268 = 0.1963\,{\rm bit} \hspace{0.05cm},$$

• die Äquivokation (oder Rückschlussentropie):

$$H(X|Y) = H(X) - I(X;Y) = 0.4690 - 0.1963 = 0.2727\,{\rm bit} \hspace{0.05cm},$$

• die Irrelevanz (oder Streuentropie):

$$H(Y|X) = H(Y) - I(X;Y) = 0.8541 - 0.1963 = 0.6578\,{\rm bit} \hspace{0.05cm}.$$

Die Ergebnisse sind in der folgenden Grafik nochmals zusammengefasst.

Anmerkung: Äquivokation und Irrelevanz hätte man auch direkt (aber mit Mehraufwand) aus den entsprechenden Wahrscheinlichkeitsfunktionen berechnen können. Zum Beispiel die Irrelevanz:

$$H(Y|X) = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.05cm}\in \hspace{0.05cm}XY} \hspace{-0.2cm} P_{XY}(x,\hspace{0.05cm}y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.03cm}X} (\hspace{0.05cm}y\hspace{0.03cm} |\hspace{0.05cm} x)}=$$

$$.\hspace{0.3cm} = p_{00} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon_0} + p_{01} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon_0} + p_{10} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon_1} + p_{11} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon_1} = 0.6578\,{\rm bit} \hspace{0.05cm}.$$

Definition und Bedeutung der Kanalkapazität

Wir betrachten weiter einen diskreten gedächtnislosen Kanal (englisch: Discrete Memoryless Channel, kurz DMC) mit einer endlichen Anzahl an Quellensymbolen ⇒ $|X|$ und ebenfalls nur endlich vielen Sinkensymbolen ⇒ $|Y|$, wie im ersten Abschnitt dieses Kapitels dargestellt. Berechnet man die Transinformation $I(X, Y)$ wie zuletzt an einem Beispiel ausgeführt, so hängt diese auch von der Quellenstatistik ⇒ $P_X(X)$ ab. Ergo: $I(X, Y)$ ist keine reine Kanalkenngröße.

Die von E. Shannon eingeführte Kanalkapazität (englisch: Channel Capacity) lautet entsprechend seinem Standardwerk :

$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$

Da nach dieser Definition stets die bestmögliche Quellenstatistik zugrunde liegt, hängt $C$ nur von den Kanaleigenschaften ⇒ $P_{Y|X}(Y|X)$ ab, nicht jedoch von $P_X(X)$. Oft wird die Zusatzeinheit „bit/Kanalzugriff” hinzugefügt, bei englischen Texten „bit/use”.

C. E. Shannon benötigte diese Kanalbeschreibungsgröße $C$, um das Kanalcodierungstheorem formulieren zu können – eines der Highlights der von ihm begründeten Informationstheorie.

Shannons Kanalcodierungstheorem: Zu jedem Übertragungskanal mit der Kanalkapazität $C$ > 0 existiert (mindestens) ein $(k, n)$–Blockcode, dessen (Block–)Fehlerwahrscheinlichkeit gegen Null geht, so lange die Coderate $R$ = $k/n$ kleiner oder gleich der Kanalkapazität ist: $R ≤ C$. Voraussetzung hierfür ist allerdings, dass für die Blocklänge dieses Codes gilt: $n → ∞$.

Den Beweis dieses Theorems finden Sie zum Beispiel in , und . Der Beweis würde den Rahmen unseres Lerntutorials sprengen.

Im Kapitel 4.3 wird im Zusammenhang mit dem wertkontinuierlichen AWGN–Kanalmodell ausgeführt, welche phänomenal große Bedeutung Shannons informationstheoretisches Theorem für die gesamte Informationstechnik besitzt, nicht nur für ausschließlich theoretisch Interessierte, sondern ebenso auch für Praktiker. Wie in Aufgabe A3.12 gezeigt werden soll, gilt auch der Umkehrschluss:

Ist die Rate des verwendeten ( $n$, $k$ )–Blockcodes größer als die Kanalkapazität ⇒ $\mathbf{R = k/n > C}$, so kann niemals eine beliebig kleine Blockfehlerwahrscheinlichkeit erreicht werden.

Auch diesen Beweis finden Sie zum Beispiel wieder in , und .

Kanalkapazität eines Binärkanals

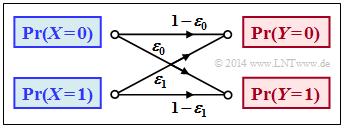Die Transinformation des allgemeinen (unsymmetrischen) Binärkanals gemäß der nebenstehenden Grafik wurde im letzten Abschnitt berechnet. Bei diesem Modell werden die Eingangssymbole „0” und „1” unterschiedlich stark verfälscht:

$$P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{-0.01cm} X) = \begin{pmatrix} 1 - \varepsilon_0 & \varepsilon_0\\ \varepsilon_1 & 1 - \varepsilon_1 \end{pmatrix} \hspace{0.05cm}.$$

Die Transinformation lässt sich mit $P_X(X)$ = $(p_0, p_1)$ in folgender Form kompakt darstellen:

$$\begin{align*}I(X ;Y) = \sum_{\mu = 1}^{2} \hspace{0.1cm}\sum_{\kappa = 1}^{2} \hspace{0.2cm} {\rm Pr} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu}) \cdot {\rm Pr} (\hspace{0.05cm}x_{\mu}\hspace{0.05cm})\cdot {\rm log}_2 \hspace{0.1cm} \frac{{\rm Pr} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu})}{{\rm Pr} (\hspace{0.05cm}y_{\kappa})} = \\ & = \hspace{-0.15cm} (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0) \cdot p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0}{(1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0) \cdot p_0 + \varepsilon_1 \cdot p_1} + \varepsilon_0 \cdot p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{\varepsilon_0}{(1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0) \cdot p_0 + \varepsilon_1 \cdot p_1} + \\ & + \hspace{-0.15cm} \varepsilon_1 \cdot p_1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{\varepsilon_1}{\varepsilon_0 \cdot p_0 + (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1) \cdot p_1} + (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1) \cdot p_1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1}{\varepsilon_0 \cdot p_0 + (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1) \cdot p_1} \hspace{0.05cm}.\end{align*}$$

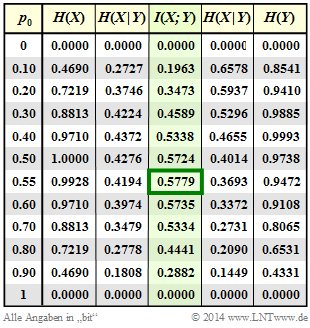
Im Folgenden setzen wir $ε_0$ = 0.01 und $ε_1$ = 0.2. In der vierten Spalte der nebenstehenden Tabelle (grün hinterlegt) ist die Transinformation $I(X; Y)$ dieses unsymmetrischen Binärkanals abhängig von der Quellensymbolwahrscheinlichkeit $p_0$ = Pr( $X$ = 0 ) angegeben. Man erkennt:

• Die Transinformation $I(X; Y)$ hängt von den Symbolwahrscheinlichkeiten $p_0$ und $p_1$ = 1 – $p_0$ ab.
• Der Maximalwert der Transinformation ergibt sich für $p_0$ ≈ 0.55 ⇒ $p_1$ ≈ 0.45.
• Das Optimierungsergebnis $p_0 > p_1$ folgt aus der Relation $ε_0 < ε_1$ (die „0” wird weniger verfälscht).
• Die Kanalkapazität ist somit für $ε_0$ = 0.01, $ε_1$ = 0.2 gleich $C$ = 0.5779 bit/Kanalzugriff.

In obiger Gleichung ist als Sonderfall auch der Binary Symmetric Channel (BSC) mit dem Parameter $ε$ = $ε_0$ = $ε_1$ mitenthalten. In Aufgabe A3.9 wird die Transinformation des BSC–Kanals für $ε$ = 0.1, $p_0$ = 0.2 berechnet und in Aufgabe Z3.9 seine Kanalkapazität wie folgt angegeben:

$$C_{\rm BSC} = 1 - H_{\rm bin} (\varepsilon) \hspace{0.05cm}.$$

Eigenschaften symmetrischer Kanäle

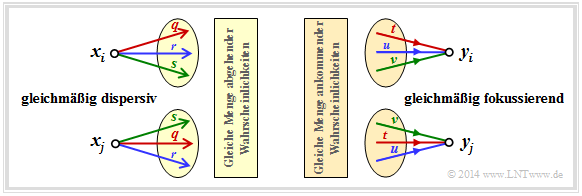
Die Kapazitätsberechnung des (allgemeinen) diskreten gedächtnislosen Kanals ist oftmals aufwändig. Sie vereinfacht sich entscheidend, wenn Symmetrien des Kanals ausgenutzt werden. Die Grafik zeigt zwei Beispiele.

• Beim gleichmäßig dispersiven Kanal (englisch: Uniformly Dispersive Channel) ergibt sich für alle Quellensymbole $x ∈ X$ die genau gleiche Menge an Übergangswahrscheinlichkeiten ⇒ $\{P_Y|X(y_κ|x)\}$ mit 1 ≤ $κ$ ≤ $|Y|$. In der linken Grafik ist dies durch die Werte $q$, $r$ und $s$ mit $q + r + s$ = 1 angedeutet.
• Beim gleichmäßig fokussierenden Kanal (englisch: Uniformely Focusing Channel) ergibt sich für alle Sinkensymbole $y ∈ Y$ die gleiche Menge an Übergangswahrscheinlichkeiten ⇒ $\{P_Y|X(y|x_μ)\}$ mit 1 ≤ $μ$ ≤ $|X|$. Hier muss nicht notwendigerweise $t + u + v$ = 1 gelten (siehe rechte Grafik).

Ist ein diskreter gedächtnisloser Kanal sowohl gleichmäßig dispersiv als auch gleichmäßig fokussierend, so liegt ein streng symmetrischer Kanal (englisch: Strongly Symmetric Channel) vor. Bei gleichverteiltem Quellenalphabet besitzt dieser die Kapazität

$$C = {\rm log}_2 \hspace{0.1cm} |Y| + \sum_{y \hspace{0.05cm}\in\hspace{0.05cm} Y} \hspace{0.1cm} P_{\hspace{0.01cm}Y \mid \hspace{0.01cm} X}(y|x) \cdot {\rm log}_2 \hspace{0.1cm}P_{\hspace{0.01cm}Y \mid \hspace{0.01cm} X}(y|x) \hspace{0.05cm}.$$

Für diese Gleichung kann jedes beliebige $x ∈ X$ herangezogen werden.

Diese Definition soll durch ein Beispiel verdeutlicht werden.

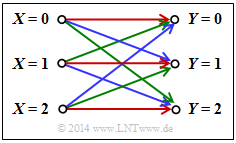Beim betrachteten Kanal bestehen Verbindungen zwischen allen $|X|$ = 3 Eingängen und allen $|Y|$ = 3 Ausgängen:

• Eine rote Verbindung steht für $P_{Y|X}(y_κ|x_μ)$ = 0.7.
• Eine blaue Verbindung steht für $P_{Y|X}(y_κ|x_μ)$ = 0.2.
• Eine grüne Verbindung steht für $P_{Y|X}(y_κ|x_μ)$ = 0.1.

Nach obiger Gleichung gilt dann für die Kanalkapazität:

$$C = {\rm log}_2 \hspace{0.1cm} (3) + 0.7 \cdot {\rm log}_2 \hspace{0.1cm} (0.7) + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} (0.2) + 0.1 \cdot {\rm log}_2 \hspace{0.1cm} (0.1) = 0.4282 \,\,{\rm bit} \hspace{0.05cm}.$$

Hinweis: Der Zusatz „die gleiche Menge an Übergangswahrscheinlichkeiten” bedeutet nicht, dass $P_Y|X(y_κ|x_1)$ = $P_Y|X(y_κ|x_2)$ = $P_Y|X(y_κ|x_3)$ gelten muss. Vielmehr geht in diesem Beispiel von jedem Eingang ein roter, ein blauer und ein grüner Pfeil ab und an jeden Ausgang kommt ein roter, ein blauer und ein grüner Pfeil an. Die jeweiligen Reihenfolgen permutieren. R – G – B, B – R – G, G – B – R.

Ein Beispiel für einen streng symmetrischen Kanal ist der Binary Symmetric Channel (BSC). Dagegen ist der Binary Erasure Channel (BEC) nicht streng symmetrisch, da er

• zwar gleichmäßig dispersiv ist,
• aber nicht gleichmäßig fokussierend.

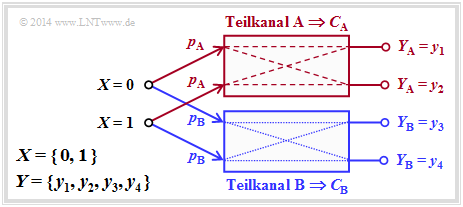
Nachfolgende Definition ist weniger restriktiv als die vorherige des streng symmetrischen Kanals.

Ein symmetrischer Kanal (englisch: Symmetric Channel) liegt vor, wenn er in mehrere (allgemein $L$) streng symmetrische Teilkanäle aufgeteilt werden kann, indem das Ausgangsalphabet $Y$ in $L$ Teilmengen $Y_1$, ..., $Y_L$ aufgespalten wird. Ein solcher symmetrischer Kanal besitzt folgende Kapazität:

$$C = \sum_{l \hspace{0.05cm}=\hspace{0.05cm} 1}^{L} \hspace{0.1cm} p_l \cdot C_l \hspace{0.05cm}.$$

Hierbei sind folgende Bezeichnungen verwendet:

• $p_l$ gibt die Wahrscheinlichkeit an, dass der $l$–te Teilkanal ausgewählt wird,
• $C_l$ ist die Kanalkapazität dieses $l$–ten Teilkanals.

Die Grafik verdeutlicht diese Definition für $L$ = 2, wobei die Teilkanäle mit A und B bezeichnet sind. An den unterschiedlich gezeichneten Übergängen (gestrichelt oder gepunktet) erkennt man, dass die zwei Teilkanäle durchaus verschieden sind, so dass $C_A$ ≠ $C_B$ gelten wird.

Für die Kapazität des Gesamtkanals erhält man somit allgemein:

$$C = p_{\rm A} \cdot C_{\rm A} + p_{\rm B} \cdot C_{\rm B} \hspace{0.05cm}.$$

Über die Struktur der beiden Teilkanäle wird hier keine Aussage gemacht. Im Beispiel auf der nächsten Seite wird sich zeigen, dass auch der BEC durch diese Grafik grundsätzlich beschreibbar ist. Allerdings müssen dann die zwei Ausgangssysmbole $y_3$ und $y_4$ zu einem einzigen Symbol zusammengefasst werden.

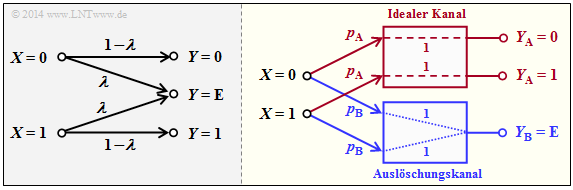
Die linke Grafik zeigt den Binary Erasure Channel (BEC) mit Eingang $X$ = {0, 1} und Ausgang $Y$ = {0, 1, $E$}, wie er meistens gezeichnet wird. Teilt man diesen entsprechend der rechten Grafik auf in einen idealen Kanal $(y = x)$ mit $y ∈ Y_A$ = {0, 1} ⇒ $C_A$ = 1 bit, einen Auslöschungskanal mit $y ∈ Y_B$ = $\{E \}$ ⇒ $C_B$ = 0, so ergibt sich mit den Teilkanalgewichtungen $p_A$ = 1 – $λ$ und $p_B$ = $λ$ für die Kanalkapazität:

$$C_{\rm BEC} = p_{\rm A} \cdot C_{\rm A} = 1 - \lambda \hspace{0.05cm}.$$

Beide Kanäle sind streng symmetrisch. Für den (idealen) Kanal A gilt gleichermaßen

• für $X = 0$ und $X = 1$: $\text{Pr}(Y = 0|X) = \text{Pr}(Y = 1|X) = 1 – λ$ ⇒ gleichmäßig dispersiv,
• für $Y = 0$ und $Y = 1$: $\text{Pr}(Y|X = 0) = Pr(Y|X = 1) = 1 – λ$ ⇒ gleichmäßig fokussierend.

Entsprechendes gilt für den Auslöschungskanal B.

In Aufgabe A3.11 wird sich zeigen, dass die Kapazität des Kanalmodells Binary Symmetric Error & Erasure Channel (BSEC) in gleicher Weise berechnet werden kann. Mit

• der Verfälschungswahrscheinlichkeit $ε$ und
• der Auslöschungswahrscheinlichkeit $λ$

erhält man in diesem Fall:

$$C_{\rm BSEC} = (1- \lambda) \cdot \left [ 1 - H_{\rm bin}(\frac{\varepsilon}{1- \lambda}) \right ]\hspace{0.05cm}.$$

Einige Grundlagen der Kanalcodierung

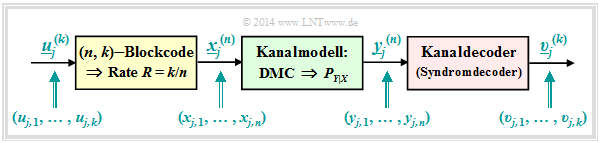
Um das Kanalcodierungstheorem richtig interpretieren zu können, sind einige Grundlagen der Kanalcodierung (englisch: Channel Coding) erforderlich. Dieses äußerst wichtige Gebiet der Nachrichtentechnik wird in einem eigenen Buch Kanalcodierung behandelt. Die nachfolgende Beschreibung bezieht sich auf das stark vereinfachte Modell für binäre Blockcodes:

Zu diesem Blockschaltbild ist anzumerken:

• Die unendlich lange Quellensymbolfolge $\underline{u}$ (hier nicht dargestellt) wird in Blöcke zu jeweils $k$ bit unterteilt. Wir bezeichnen den Informationsblock mit der laufenden Nummerierung $j$ mit $\underline{u}_j^{(k)}$.
• Jeder Informationsblock $j$ mit $\underline{u}_j^{(k)}$ wird durch den gelb hinterrlegten Kanalcoder in ein Codewort $\underline{x}_j^{(n)}$ umgesetzt, wobei $n > k$ gelten soll. Das Verhältnis $R = k/n$ bezeichnet man als die Coderate.
• Der Discrete Memoryless Channel (DMC) wird durch die Übergangswahrscheinlichkeit $P_{Y|X}(⋅)$ berücksichtigt. Dieser grün hinterlegte Block bewirkt Fehler auf Bitebene ⇒ $y_{j, i} ≠ x_{j, i}$.
• Damit unterscheiden sich auch die aus $n$ Bit bestehenden Empfangsblöcke $\underline{y}_j^{(n)}$ von den Codeworten $\underline{x}_j^{(n)}$. Ebenso gilt im allgemeinen für die Blöcke nach dem Deoder: $\underline{v}_j^{(k)} ≠ \underline{u}_j^{(k)}$.

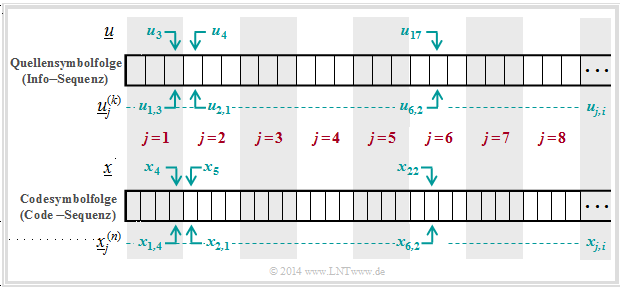
Die Grafik soll die hier verwendete Nomenklatur am Beispiel $k$ = 3, $n$ = 4 verdeutlichen. Dargestellt sind die jeweils ersten acht Blöcke der Informationssequenz $\underline{u}$ und der Codesequenz $\underline{x}$. Man erkennt folgende Zuordnung zwischen der geblockten und der ungeblockten Beschreibung:

• Bit 3 des 1. Info–Blocks ⇒ $u_{1, 3}$ entspricht dem Symbol u3 in ungeblockter Darstellung.
• Bit 1 des 2. Info–Blocks ⇒ $u_{2, 1}$ entspricht dem Symbol $u_4$ in ungeblockter Darstellung.
• Bit 2 des 6. Info–Blocks ⇒ $u_{6, 2}$ entspricht dem Symbol $u_{17}$ in ungeblockter Darstellung.
• Bit 4 des 1. Codewortes ⇒ $x_{1, 4}$ entspricht dem Symbol $x_4$ in ungeblockter Darstellung.
• Bit 1 des 2. Codewortes ⇒ $x_{2, 1}$ entspricht dem Symbol $x_5$ in ungeblockter Darstellung.
• Bit 2 des 6. Codewortes ⇒ $x_{6, 2}$ entspricht dem Symbol $x_{22}$ in ungeblockter Darstellung.

Zur Interpretation des Kanalcodierungstheorems benötigen wir noch verschiedene Definitionen für „Fehlerwahrscheinlichkeiten”. Aus dem Systemmodell lassen sich folgende Größen ableiten:

• Die Kanalfehlerwahrscheinlichkeit ergibt sich beim vorliegenden Kanalmodell zu

$${\rm Pr(Kanalfehler)} = {\rm Pr} \left ({y}_{j,\hspace{0.05cm} i} \ne {x}_{j,\hspace{0.05cm} i} \right )\hspace{0.05cm}.$$

Beispielsweise ist beim BSC–Modell Pr(Kanalfehler) = $ε$ für alle $j$ = 1, 2, ... und 1 ≤ $i$ ≤ $n$.

• Die Blockfehlerwahrscheinlichkeit bezieht sich auf die zugeordneten Informationsblöcke am Codereingang ⇒ $\underline{u}_j^{(k)}$ und am Decoderausgang ⇒ $\underline{v}_j^{(k)}$, jeweils in Blöcken zu $k$ Bit:

$${\rm Pr(Blockfehler)} = {\rm Pr} \left (\underline{\upsilon}_j^{(k)} \ne \underline{u}_j^{(k)} \right )\hspace{0.05cm}.$$

• Die Bitfehlerwahrscheinlichkeit bezieht sich ebenfalls auf den Eingang und den Ausgang des betrachteten Codiersystems, allerdings auf Bitebene:

$${\rm Pr(Bitfehler)} = {\rm Pr} \left ({\upsilon}_{j,\hspace{0.05cm} i} \ne {u}_{j,\hspace{0.05cm} i} \right )\hspace{0.05cm}.$$

Hierbei ist vereinfachend vorausgesetzt, dass alle $k$ Bit $u_{j,i}$ des Informationsblockes $j$ mit gleicher Wahrscheinlichkeit verfälscht werden (1 ≤ $i$ ≤ $k$). Andernfalls müsste über die $k$ Bit gemittelt werden.

Zwischen Blockfehler– und Bitfehlerwahrscheinlichkeit besteht allgemein der Zusammenhang:

$${1}/{k} \cdot {\rm Pr(Blockfehler)} \le {\rm Pr(Bitfehler)} \le {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$

• Die untere Schranke ergibt sich, wenn bei allen fehlerhaften Blöcken alle Bit falsch sind.
• Gibt es in jedem fehlerhaften Block genau nur einen einzigen Bitfehler, dann ist die Bitfehlerwahrscheinlichkeit Pr(Bitfehler) identisch mit der Blockfehlerwahrscheinlichkeit Pr(Blockfehler).

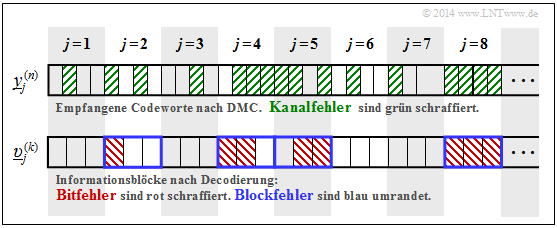
Die Grafik zeigt oben die ersten acht Empfangsblöcke $\underline{y}_j^{(n)}$ mit $n$ = 4. Kanalfehler sind grün schraffiert. Unten ist die Ausgangsfolge $\underline{v}$ skizziert, unterteilt in Blöcke $\underline{v}_j^{(k)}$ zu je $k$ = 3 Bit:

• Bitfehler sind im unteren Diagramm rot schraffiert.
• Blockfehler erkennt man an der blauen Umrahmung.

Hierzu einige (aufgrund der kurzen Folge) vage Angaben zu den Fehlerwahrscheinlichkeiten:

• Die Hälfte der Empfangsbits sind grün schraffiert. Daraus folgt:

$${\rm Pr(Kanalfehler)} = 16/32 = 1/2.$$

• Die Bitfehlerwahrscheinlichkeit lautet mit der beispielhaften Codierung & Decodierung:

$${\rm Pr(Bitfehler)} = 8/24 = 1/3.$$

• Dagegen würde bei uncodierter Übertragung gelten:

$${\rm Pr(Bitfehler)} = {\rm Pr(Kanalfehler)} = 1/2.$$

• Die Hälfte der decodierten Blöcke sind blau umrandet. Daraus folgt:

$${\rm Pr(Blockfehler)} = 4/8 = 1/2.$$

Mit Pr(Blockfehler) = 1/2 und k = 3 liegt die Bitfehlerwahrscheinlichkeit in folgendem Bereich:

$$1/6 \le {\rm Pr(Bitfehler)} \le 1/2 \hspace{0.05cm}.$$

• Die obere Schranke ergibt sich, wenn in jedem der vier verfälschten Blöcke alle Bit falsch sind: Pr(Bitfehler) = 12/24 = 1/2.
• Die untere Schranke beschreibt den Fall, dass in jedem der vier verfälschten Blöcke jeweils nur ein Bit falsch ist: Pr(Bitfehler) = 4/24 = 1/6.

Rate, Kanalkapazität und Bitfehlerwahrscheinlichkeit

Durch Kanalcodierung wird die Zuverlässigkeit (englisch: Reliability) der Datenübertragung von der Quelle zur Sinke erhöht. Vermindert man die Coderate $R = k/n$ und erhöht so die hinzugefügte Redundanz (1 – $R$), so wird im allgemeinen die Datensicherheit verbessert und damit die Bitfehlerwahrscheinlichkeit herabgesetzt, die wir im Weiteren kurz $p_B$ nennen:

$$p_{\rm B} = {\rm Pr(Bitfehler)} = {\rm Pr} \left ({\upsilon}_{j,\hspace{0.05cm} i} \ne {u}_{j,\hspace{0.05cm} i} \right )\hspace{0.05cm}.$$

Das folgende Theorem basiert auf dem Data Processing Theorem und Fano's Lemma. Die Herleitung kann in den Standardwerken zur Informationstheorie nachgelesen werden, zum Beispiel in :

Umkehrung des Shannonschen Kanalcodierungstheorems: Benutzt man zur Datenübertragung mit Rate $R$ einen Kanal mit unzureichender Kanalkapazität $C < R$, so kann auch bei bestmöglicher Kanalcodierung die Bitfehlerwahrscheinlichkeit $p_B$ eine untere Schranke nicht unterschreiten:

$$p_{\rm B} \ge H_{\rm bin}^{-1} \cdot \left ( 1 - {C}/{R}\right ) > 0\hspace{0.05cm}.$$

$H_{\rm bin}(⋅)$ bezeichnet hierbei die binäre Entropiefunktion.

Da die Wahrscheinlichkeit der Blockfehler nie kleiner sein kann als die der Bitfehler, ist für $R > C$ auch die Blockfehlerwahrscheinlichkeit „0” nicht möglich. Aus dem angegebenen Bereich für die Bitfehler,

$${1}/{k} \cdot {\rm Pr}({\rm Blockfehler}) \le {\rm Pr}({\rm Bitfehler}) \le {\rm Pr}({\rm Blockfehler})\hspace{0.05cm},$$

lässt sich auch ein Bereich für die Blockfehlerwahrscheinlichkeit angeben:

$$ {\rm Pr}({\rm Bitfehler}) \le {\rm Pr}({\rm Blockfehler}) \le k \cdot {\rm Pr}({\rm Bitfehler})\hspace{0.05cm}.$$

Verwendet man einen Kanal mit der Kapazität $C$ = 1/3 (bit) zur Datenübertragung mit der Coderate $R$ < 1/3, so ist prinzipiell die Bitfehlerwahrscheinlichkeit $p_B$ = 0 möglich.

• Allerdings ist aus dem Kanalcodierungstheorem der spezielle ( $k$, $n$ )–Blockcode nicht bekannt, der dieses Wunschergebnis ermöglicht. Shannon macht hierzu keine Aussagen.
• Bekannt ist nur, dass ein solcher bestmöglicher Code mit unendlich langen Blöcken arbeitet. Bei gegebener Coderate $R$ = $k/n$ gilt somit sowohl $k → ∞$ als auch $n → ∞$.
• Deshalb ist die Aussage „Die Bitfehlerwahrscheinlichkeit ist 0” nicht identisch mit „Es treten keine Bitfehler auf”: Auch bei endlich vielen Bitfehlern und $k → ∞$ gilt $p_B$ = 0.

Mit der Coderate $R$ = 1 (uncodierte Übertragung) erhält man:

$$p_{\rm B} \ge H_{\rm bin}^{-1} \cdot \left ( 1 - \frac{1/3}{1.0}\right ) = H_{\rm bin}^{-1}(2/3) \approx 0.174 > 0\hspace{0.05cm}.$$

Mit der Coderate $R$ = 1/2 > $C$ ist die Bitfehlerwahrscheinlichkeit zwar kleiner, aber nicht 0:

$$p_{\rm B} \ge H_{\rm bin}^{-1} \cdot \left ( 1 - \frac{1/3}{1/2}\right ) = H_{\rm bin}^{-1}(1/3) \approx 0.062 > 0\hspace{0.05cm}.$$

Aufgabenhinweis: A3.12: Coderate und Zuverlässigkeit – A3.13: Kanalcodierungstheorem