Aufgaben:Aufgabe 3.4Z: Verschiedene Allpässe: Unterschied zwischen den Versionen
| Zeile 69: | Zeile 69: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Durch Umformung der angegebenen <i>p</i>–Übertragungsfunktion ergibt sich | |
| − | + | $$H_{\rm L}(p)= \frac {1-{p}/{A}} {1+{p}/{A}}= -1 \cdot \frac {p-A} {p+A}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\hspace{0.15cm} \underline{K =- 1}, \hspace{0,2cm} \hspace{0.15cm} \underline{p_{\rm o}/A = 1} ,\hspace{0,2cm} | |
\hspace{0.15cm} \underline{ p_{\rm x}/A = -1} \hspace{0.05cm} .$$ | \hspace{0.15cm} \underline{ p_{\rm x}/A = -1} \hspace{0.05cm} .$$ | ||
| − | + | ||
| − | + | ||
| + | '''(2)''' Setzt man $p = {\rm j} \cdot 2 \pi f$, so erhält man: | ||
| + | $$H(f)= \frac {1-{\rm j \cdot 2\pi \it | ||
f}/A} {1+{\rm j \cdot 2\pi \it | f}/A} {1+{\rm j \cdot 2\pi \it | ||
f}/A}\hspace{0.05cm} .$$ | f}/A}\hspace{0.05cm} .$$ | ||
| − | + | Der Betrag eines Quotienten ist gleich dem Quotienten der Beträge: | |
| − | + | $$|H(f)|= \frac {|1-{{\rm j} \cdot 2\pi | |
f}/A|} {|1+{\rm j \cdot 2\pi \it | f}/A|} {|1+{\rm j \cdot 2\pi \it | ||
f}/A|}= \frac {\sqrt{1+(2\pi | f}/A|}= \frac {\sqrt{1+(2\pi | ||
f/A)^2}} {\sqrt{1+(2\pi | f/A)^2}} {\sqrt{1+(2\pi | ||
f/A)^2}}= 1$$ | f/A)^2}}= 1$$ | ||
| − | + | $$\Rightarrow \hspace{0.3cm} a(f)= -{\rm ln} \hspace{0.1cm} |H(f)|= 0\hspace{0.2cm}({\rm Np \hspace{0.2cm}oder \hspace{0.2cm}dB})\hspace{0.05cm} .$$ | |
| − | + | Richtig ist somit die <u>Aussage 2</u>. Aber uch die <u>Aussage 3</u> ist richtig, wie aus der Theorieseite „Grafische Ermittlung der Dämpfung” zu ersehen ist. | |
| + | |||
| − | + | '''(3)''' Die Phasenfunktion $b(f)$ kann wie folgt berechnet werden: | |
| − | + | $$b(f)= -{\rm arc} \hspace{0.1cm} H(f) \hspace{0.25cm} = \hspace{0.2cm} {\rm arctan } \hspace{0.1cm} ({2\pi | |
| − | f}{A} - {\rm arctan } \hspace{0.1cm} | + | f}/{A}) - {\rm arctan } \hspace{0.1cm} ({-2\pi |
| − | f}{A} = 2 \cdot {\rm arctan } \hspace{0.1cm} | + | f}/{A}) = 2 \cdot {\rm arctan } \hspace{0.1cm} ({2\pi |
| − | f}{A} | + | f}/{A}),$$ |
| − | + | $$b(f= {A}/{2\pi})= 2 \cdot {\rm arctan } | |
| − | \hspace{0.1cm}(1) = 2 \cdot 45^\circ\hspace{0.15cm} \underline{ = 90^\circ}\hspace{0.05cm} | + | \hspace{0.1cm}(1) = 2 \cdot 45^\circ \hspace{0.15cm} \underline{ = 90^\circ}\hspace{0.05cm},$$ |
| − | + | $$ b(f= {A}/{\pi})=2 \cdot {\rm arctan } | |
| − | |||
\hspace{0.1cm}(2) = 2 \cdot 63.4^\circ \hspace{0.15cm} \underline{= 126.8^\circ}\hspace{0.05cm} | \hspace{0.1cm}(2) = 2 \cdot 63.4^\circ \hspace{0.15cm} \underline{= 126.8^\circ}\hspace{0.05cm} | ||
| − | , | + | ,$$ |
| − | + | $$ b(f \rightarrow \infty)=2 \cdot {\rm arctan } | |
\hspace{0.1cm}(\infty) = 2 \cdot 90^\circ \hspace{0.15cm} \underline{= 180^\circ}\hspace{0.05cm} | \hspace{0.1cm}(\infty) = 2 \cdot 90^\circ \hspace{0.15cm} \underline{= 180^\circ}\hspace{0.05cm} | ||
.$$ | .$$ | ||
| − | + | Zu den gleichen Ergebnissen kommt man nach der Vorgehensweise entsprechend der Seite „Grafische Ermittlung der Phase” im Theorieteil. | |
| + | |||
| − | + | '''(4)''' Die angegebene $p$–Übertragungsfunktion lässt sich wie folgt darstellen: | |
| − | + | $$H_{\rm L}(p)= \frac {Z_2-Z_1} {Z_1+2 \cdot \sqrt{Z_1 \cdot Z_2}+Z_2}= | |
| − | + | \frac {(\sqrt{Z_2}-\sqrt{Z_1})(\sqrt{Z_2}+\sqrt{Z_1})} {(\sqrt{Z_2}+\sqrt{Z_1})^2}= | |
\frac {\sqrt{Z_2}-\sqrt{Z_1}} {\sqrt{Z_2}+\sqrt{Z_1}}\hspace{0.05cm}.$$ | \frac {\sqrt{Z_2}-\sqrt{Z_1}} {\sqrt{Z_2}+\sqrt{Z_1}}\hspace{0.05cm}.$$ | ||
| − | + | Mit $Z_1 = p \cdot L$ und $Z_2 = 1/(p \cdot C)$ erhält man weiter: | |
| − | + | $$H_{\rm L}(p)= \frac {\sqrt{{1}/(pC)}-\sqrt{pL}} {\sqrt{{1}/(pC)}+\sqrt{pL}} | |
= \frac {1- p \cdot \sqrt{LC}} {1+ p \cdot \sqrt{LC}} | = \frac {1- p \cdot \sqrt{LC}} {1+ p \cdot \sqrt{LC}} | ||
= -1 \cdot \frac {p-\sqrt{{1}/(LC)}} {p+\sqrt{{1}/(LC)}}$$ | = -1 \cdot \frac {p-\sqrt{{1}/(LC)}} {p+\sqrt{{1}/(LC)}}$$ | ||
| − | + | $$\Rightarrow \hspace{0.3cm}A = \sqrt{{1}/(LC)}: \hspace{0.2cm}H_{\rm L}(p)= -1 \cdot \frac {p-A} {p+A}\hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Es ergibt sich die genau gleiche Übertragungsfunktion, wie in der Teilaufgabe (1) berechnet. Daraus folgt, dass nur die <u>Aussage 1</u> richtig ist: | |
| + | *Der Dämpfungsverlauf ist $a(f) == 0\ \rm (Np)$. Keine Frequenz wird gedämpft oder verstärkt. Man spricht deshalb auch von einem „Allpass”. | ||
| + | *Die zweite Aussage ist falsch. Der Phasenverlauf $b(f)$ ist nicht linear, sondern vielmehr wie in der Teilaufgabe (3) berechnet. | ||
| + | *Die Hilbert–Transformierte der Konstanten $a(f) = 0$ müsste zur Phasenfunktion $b(f) = 0$ führen, wie im Theorieteil gezeigt. Das heißt, dass die Aussage 3 falsch ist. | ||
| + | *Nur bei minimalphasigen Systemen hängen die Dämpfungsfunktion $a(f)$ und Phasenfunktion $b(f)$ über die Hilbert–Transformation zusammen. | ||
| + | *Bei einem solchen Minimum–Phasen–System liegen aber alle Pole und Nullstellen in der linken $p$–Halbebene, was hier nicht zutrifft ⇒ ein Allpass ist kein Minimum–Phasen–System. | ||
| − | |||
| − | + | '''(5)''' <u>Beide Aussagen</u> sind richtig: | |
| + | *Wie bereits in der Teilaufgabe (2) festgestellt wurde, ergibt sich immer dann eine konstante Dämpfung, wenn es zu jedem Pol in der linken $p$–Halbebene eine entsprechende Nullstelle in der rechten Halbebene gibt ⇒ die Schaltung <b>B</b> zeigt ebenfalls Allpass–Charakteristik. | ||
| + | *Da $b(f)$ stets eine unsymmetrische Funktion ist, gilt $b(f= 0) = 0$ ganz allgemein, das heißt für jede Spektralfunktion $H(f)$, deren Fourier–Rücktransformierte reell ist. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 10. Februar 2017, 15:43 Uhr
Wir gehen zunächst von einem Vierpol mit der folgenden Übertragungsfunktion aus: $$H_{\rm L}(p)= \frac {1-{p}/{A}} {1+{p}/{A}}.$$ Aus dieser soll der herkömmliche Fourier–Frequenzgang $$H(f) = {\rm e}^{-a(f)\hspace{0.05cm}}\cdot {\rm e}^{- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}$$ ermittelt werden, der sich durch Dämpfungsfunktion $a(f)$ und Phasenfunktion $b(f)$ darstellen lässt.
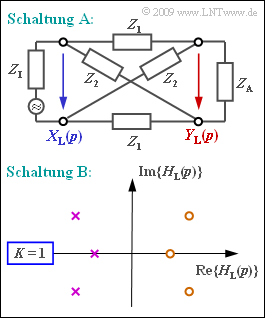
Die obere Grafik zeigt eine so genannte Allpass–Schaltung, wobei der komplexe Widerstand $Z_1$ eine Induktivität und $Z_2$ eine Kapazität bezeichnet: $$Z_1 = p \cdot L\hspace{0.05cm},\hspace{0.2cm}Z_2 = \frac{1}{p \cdot C}\hspace{0.05cm}.$$ Bei reflexionsfreier Anpassung am Eingang und Ausgang mit $$Z_{\rm I}=Z_{\rm A} = \sqrt{Z_1 \cdot Z_2} = \sqrt{{L}/{C}}$$ gilt für die p–Übertragungsfunktion der Schaltung A (siehe obere Grafik): $$H_{\rm L}(p)= \frac {Y_{\rm L}(p)} {X_{\rm L}(p)}= \frac {Z_2-Z_1} {Z_1+2 \cdot \sqrt{Z_1 \cdot Z_2}+Z_2}\hspace{0.05cm}.$$
Die Schaltung B ist durch die $p$–Übertragungsfunktion festgelegt. Sie ist dadurch charakterisiert, dass
- alle Pole (in der linken $p$–Halbebene)
- spiegelbildlich zu den Nullstellen (in der rechten Halbebene) liegen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Laplace–Transformation und p–Übertragungsfunktion.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
(2) Setzt man $p = {\rm j} \cdot 2 \pi f$, so erhält man:
$$H(f)= \frac {1-{\rm j \cdot 2\pi \it
f}/A} {1+{\rm j \cdot 2\pi \it
f}/A}\hspace{0.05cm} .$$
Der Betrag eines Quotienten ist gleich dem Quotienten der Beträge:
$$|H(f)|= \frac {|1-{{\rm j} \cdot 2\pi
f}/A|} {|1+{\rm j \cdot 2\pi \it
f}/A|}= \frac {\sqrt{1+(2\pi
f/A)^2}} {\sqrt{1+(2\pi
f/A)^2}}= 1$$
$$\Rightarrow \hspace{0.3cm} a(f)= -{\rm ln} \hspace{0.1cm} |H(f)|= 0\hspace{0.2cm}({\rm Np \hspace{0.2cm}oder \hspace{0.2cm}dB})\hspace{0.05cm} .$$
Richtig ist somit die Aussage 2. Aber uch die Aussage 3 ist richtig, wie aus der Theorieseite „Grafische Ermittlung der Dämpfung” zu ersehen ist.
(3) Die Phasenfunktion $b(f)$ kann wie folgt berechnet werden:
$$b(f)= -{\rm arc} \hspace{0.1cm} H(f) \hspace{0.25cm} = \hspace{0.2cm} {\rm arctan } \hspace{0.1cm} ({2\pi
f}/{A}) - {\rm arctan } \hspace{0.1cm} ({-2\pi
f}/{A}) = 2 \cdot {\rm arctan } \hspace{0.1cm} ({2\pi
f}/{A}),$$
$$b(f= {A}/{2\pi})= 2 \cdot {\rm arctan }
\hspace{0.1cm}(1) = 2 \cdot 45^\circ \hspace{0.15cm} \underline{ = 90^\circ}\hspace{0.05cm},$$
$$ b(f= {A}/{\pi})=2 \cdot {\rm arctan }
\hspace{0.1cm}(2) = 2 \cdot 63.4^\circ \hspace{0.15cm} \underline{= 126.8^\circ}\hspace{0.05cm}
,$$
$$ b(f \rightarrow \infty)=2 \cdot {\rm arctan }
\hspace{0.1cm}(\infty) = 2 \cdot 90^\circ \hspace{0.15cm} \underline{= 180^\circ}\hspace{0.05cm}
.$$
Zu den gleichen Ergebnissen kommt man nach der Vorgehensweise entsprechend der Seite „Grafische Ermittlung der Phase” im Theorieteil.
(4) Die angegebene $p$–Übertragungsfunktion lässt sich wie folgt darstellen:
$$H_{\rm L}(p)= \frac {Z_2-Z_1} {Z_1+2 \cdot \sqrt{Z_1 \cdot Z_2}+Z_2}=
\frac {(\sqrt{Z_2}-\sqrt{Z_1})(\sqrt{Z_2}+\sqrt{Z_1})} {(\sqrt{Z_2}+\sqrt{Z_1})^2}=
\frac {\sqrt{Z_2}-\sqrt{Z_1}} {\sqrt{Z_2}+\sqrt{Z_1}}\hspace{0.05cm}.$$
Mit $Z_1 = p \cdot L$ und $Z_2 = 1/(p \cdot C)$ erhält man weiter:
$$H_{\rm L}(p)= \frac {\sqrt{{1}/(pC)}-\sqrt{pL}} {\sqrt{{1}/(pC)}+\sqrt{pL}}
= \frac {1- p \cdot \sqrt{LC}} {1+ p \cdot \sqrt{LC}}
= -1 \cdot \frac {p-\sqrt{{1}/(LC)}} {p+\sqrt{{1}/(LC)}}$$
$$\Rightarrow \hspace{0.3cm}A = \sqrt{{1}/(LC)}: \hspace{0.2cm}H_{\rm L}(p)= -1 \cdot \frac {p-A} {p+A}\hspace{0.05cm}.$$
Es ergibt sich die genau gleiche Übertragungsfunktion, wie in der Teilaufgabe (1) berechnet. Daraus folgt, dass nur die Aussage 1 richtig ist:
- Der Dämpfungsverlauf ist $a(f) == 0\ \rm (Np)$. Keine Frequenz wird gedämpft oder verstärkt. Man spricht deshalb auch von einem „Allpass”.
- Die zweite Aussage ist falsch. Der Phasenverlauf $b(f)$ ist nicht linear, sondern vielmehr wie in der Teilaufgabe (3) berechnet.
- Die Hilbert–Transformierte der Konstanten $a(f) = 0$ müsste zur Phasenfunktion $b(f) = 0$ führen, wie im Theorieteil gezeigt. Das heißt, dass die Aussage 3 falsch ist.
- Nur bei minimalphasigen Systemen hängen die Dämpfungsfunktion $a(f)$ und Phasenfunktion $b(f)$ über die Hilbert–Transformation zusammen.
- Bei einem solchen Minimum–Phasen–System liegen aber alle Pole und Nullstellen in der linken $p$–Halbebene, was hier nicht zutrifft ⇒ ein Allpass ist kein Minimum–Phasen–System.
(5) Beide Aussagen sind richtig:
- Wie bereits in der Teilaufgabe (2) festgestellt wurde, ergibt sich immer dann eine konstante Dämpfung, wenn es zu jedem Pol in der linken $p$–Halbebene eine entsprechende Nullstelle in der rechten Halbebene gibt ⇒ die Schaltung B zeigt ebenfalls Allpass–Charakteristik.
- Da $b(f)$ stets eine unsymmetrische Funktion ist, gilt $b(f= 0) = 0$ ganz allgemein, das heißt für jede Spektralfunktion $H(f)$, deren Fourier–Rücktransformierte reell ist.