Aufgaben:Aufgabe 3.6Z: Zwei imaginäre Pole: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) K (Nabil verschob die Seite Zusatzaufgaben:3.6 Zwei imaginäre Pole nach 3.6Z Zwei imaginäre Pole) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
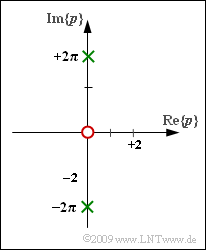
| − | [[Datei:P_ID1786__LZI_Z_3_6.png|right|]] | + | [[Datei:P_ID1786__LZI_Z_3_6.png|right|Zwei imaginäre Polstellen und eine Nullstelle ]] |
| − | + | In dieser Aufgabe betrachten wir ein kausales Signal $x(t)$ mit der Laplace–Transformierten | |
| − | + | $$X_{\rm L}(p) = | |
\frac { p} { p^2 + 4 \pi^2}= | \frac { p} { p^2 + 4 \pi^2}= | ||
\frac { p} { (p-{\rm j} \cdot 2\pi)(p+{\rm j} \cdot 2\pi)} | \frac { p} { (p-{\rm j} \cdot 2\pi)(p+{\rm j} \cdot 2\pi)} | ||
\hspace{0.05cm}$$ | \hspace{0.05cm}$$ | ||
| − | + | entsprechend der Grafik (eine rote Nullstelle und zwei grüne Pole). | |
| + | |||
| + | Das Signal $y(t)$ besitze dagegen die Laplace–Spektralfunktion | ||
:$$Y_{\rm L}(p) = | :$$Y_{\rm L}(p) = | ||
\frac { 1} { p^2 + 4 \pi^2} | \frac { 1} { p^2 + 4 \pi^2} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Die rote Nullstelle gehört somit nicht zu $Y_{\rm L}(p)$. | |
| − | + | Abschließend wird noch das Signal $z(t)$ mit der Laplace–Transformierten | |
| − | + | $$Z_{\rm L}(p) = | |
\frac { p} { (p-{\rm j} \cdot \beta)(p+{\rm j} \cdot \beta)} | \frac { p} { (p-{\rm j} \cdot \beta)(p+{\rm j} \cdot \beta)} | ||
\hspace{0.05cm}$$ | \hspace{0.05cm}$$ | ||
| − | + | betrachtet, insbesondere der Grenzfall für $\beta → 0$. | |
| − | : | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation|Laplace–Rücktransformation]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Die Frequenzvariable $p$ ist so normiert, dass nach Anwendung des Residuensatzes die Zeit $t$ in Mikrosekunden angegeben ist. | ||
| + | *Ein Ergebnis $t = 1$ ist somit als $t = T$ mit $T = 1 \ \rm \mu s$ zu interpretieren. | ||
| + | *Der [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation#Formulierung_des_Residuensatzes|Residuensatz]] lautet am Beispiel der Funktion $X_{\rm L}(p)$ mit zwei einfachen Polstellen bei $ \pm {\rm j} \cdot \beta$: | ||
:$$x(t) = X_{\rm L}(p) \cdot (p - {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p | :$$x(t) = X_{\rm L}(p) \cdot (p - {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p | ||
\hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm} \it | \hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm} \it | ||
| Zeile 33: | Zeile 40: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie das Signal | + | {Berechnen Sie das Signal $x(t)$. Welche der folgenden Aussagen sind richtig? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $x(t)$ ist ein kausales Cosinussignal. |
| − | - | + | - $x(t)$ ist ein kausales Sinussignal. |
| − | + Die Amplitude von | + | + Die Amplitude von $x(t)$ ist $1$. |
| − | + Die Periodendauer von | + | + Die Periodendauer von $x(t)$ ist $T = 1 \ \rm \mu s$. |
| − | {Berechnen Sie das Signal | + | {Berechnen Sie das Signal $y(t)$. Welche der folgenden Aussagen sind richtig? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $y(t)$ ist ein kausales Cosinussignal. |
| − | + | + | + $y(t)$ ist ein kausales Sinussignal. |
| − | - Die Amplitude von | + | - Die Amplitude von $y(t)$ ist $1$. |
| − | + Die Periodendauer von | + | + Die Periodendauer von $y(t)$ ist $T = 1 \ \rm \mu s$. |
| − | {Welche Aussagen treffen für das Signal | + | {Welche Aussagen treffen für das Signal $z(t)$ zu? |
|type="[]"} | |type="[]"} | ||
| − | + Für | + | + Für $ \beta > 0$ verläuft $z(t)$ cosinusförmig. |
| − | - Für | + | - Für $ \beta > 0$ verläuft $z(t)$ sinusförmig. |
| − | + Der Grenzfall | + | + Der Grenzfall $\beta → 0$ führt zur Sprungfunktion. |
Version vom 13. Februar 2017, 13:35 Uhr
In dieser Aufgabe betrachten wir ein kausales Signal $x(t)$ mit der Laplace–Transformierten $$X_{\rm L}(p) = \frac { p} { p^2 + 4 \pi^2}= \frac { p} { (p-{\rm j} \cdot 2\pi)(p+{\rm j} \cdot 2\pi)} \hspace{0.05cm}$$ entsprechend der Grafik (eine rote Nullstelle und zwei grüne Pole).
Das Signal $y(t)$ besitze dagegen die Laplace–Spektralfunktion
- $$Y_{\rm L}(p) = \frac { 1} { p^2 + 4 \pi^2} \hspace{0.05cm}.$$
Die rote Nullstelle gehört somit nicht zu $Y_{\rm L}(p)$.
Abschließend wird noch das Signal $z(t)$ mit der Laplace–Transformierten $$Z_{\rm L}(p) = \frac { p} { (p-{\rm j} \cdot \beta)(p+{\rm j} \cdot \beta)} \hspace{0.05cm}$$ betrachtet, insbesondere der Grenzfall für $\beta → 0$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Laplace–Rücktransformation.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Die Frequenzvariable $p$ ist so normiert, dass nach Anwendung des Residuensatzes die Zeit $t$ in Mikrosekunden angegeben ist.
- Ein Ergebnis $t = 1$ ist somit als $t = T$ mit $T = 1 \ \rm \mu s$ zu interpretieren.
- Der Residuensatz lautet am Beispiel der Funktion $X_{\rm L}(p)$ mit zwei einfachen Polstellen bei $ \pm {\rm j} \cdot \beta$:
- $$x(t) = X_{\rm L}(p) \cdot (p - {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm} \it \beta}}+X_{\rm L}(p) \cdot (p + {\rm j} \cdot \beta) \cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm}t} \Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{-\rm j \hspace{0.05cm} \it \beta}} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- 1. Durch Anwendung des Residuensatzes erhält man für das Signal x(t) bei positiven Zeiten:
- $$x_1(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= \frac {p} { p+{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= \frac{1}{2} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}\hspace{0.05cm} ,\\ x_2(t)\hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} \hspace{0.7cm}\{X_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= \frac {p} { p-{\rm j} \cdot 2\pi}\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= -{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2\pi}= \frac{1}{2} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t} \hspace{0.05cm} .$$
- $$\Rightarrow \hspace{0.3cm} x(t) = x_1(t) + x_2(t) = \frac{1}{2} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}+{\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi t}\right ] = \cos(2\pi t) \hspace{0.05cm} .$$
- Richtig sind somit die Lösungsvorschläge 1, 3 und 4.
- 2. Prinzipiell könnte diese Teilaufgabe in gleicher Weise gelöst werden wie die Teilaufgabe a). Man kann aber auch den Integrationssatz heranziehen. Dieser besagt unter anderem, dass die Multiplikation mit 1/p im Spektralbereich der Integration im Zeitbereich entspricht:
- $$Y_{\rm L}(p) = \frac{1}{p} \cdot X_{\rm L}(p) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} t \ge 0:\quad y(t) = \int\limits_{-\infty}^t \cos(2\pi \tau)\,\,{\rm d}\tau = \frac{1}{2\pi} \cdot \sin(2\pi t) \hspace{0.05cm} .$$
- Richtig sind dementsprechend die Lösungsalternativen 2 und 4.
- Hinweis: Das kausale Cosinussignal x(t) sowie das hier berechnete kausale Sinussignal y(t) sind auf dem Angabenblatt zu Aufgabe A3.6 als cK(t) bzw. sK(t) dargestellt.
- 3. Ein Vergleich mit der Berechnung von x(t) zeigt, dass z(t) = cos (β · t) für t ≥ 0 und z(t) = 0 für t < 0 gilt. Der Grenzübergang für β → 0 führt damit zur Sprungfunktion γ(t) ⇒ Lösungsvorschläge 1 und 3. Zum gleichen Ergebnis kommt man durch die Betrachtung im Spektralbereich:
- $$Z_{\rm L}(p) = \lim_{\beta \hspace{0.05cm} \rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}\frac{p}{p^2 + \beta^2} = \frac{1}{p} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z(t) = \gamma(t) \hspace{0.05cm} .$$