Aufgaben:Aufgabe 1.2: Schaltlogik (D/B-Wandler)

• Zurück zum Buch

A1.2 Schaltlogik (D/B-Wandler)

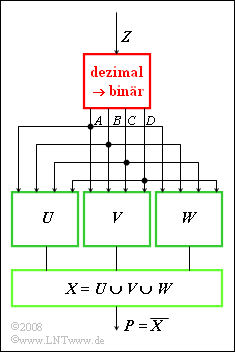
Ein Zahlengenerator $Z$ liefert Dezimalwerte im Bereich von $1$ bis $15$. Diese werden in Binärzahlen umgewandelt (rot umrandeter Block). Der Ausgang besteht aus den vier Binärwerten $A$, $B$, $C$ und $D$ mit abnehmender Wertigkeit. Beispielsweise liefert $Z = 11$ die Binärwerte $$ A = 1, \ B = 0, \ C = 1, \ D = 1. $$ Mengentheoretisch lässt sich dies wie folgt darstellen: $$ Z = 11\qquad\widehat{=}\qquad A \cap\overline{ B} \cap C \cap D$$

Aus den binären Größen $A$, $B$, $C$ und $D$ werden drei weitere Boolsche Ausdrücke gebildet, deren Vereinigungsmenge mit X bezeichnet wird: \[ U = A \cap \overline{D} \] \[ V = \overline{A} \cap B \cap \overline{D} \] $$W,\; {\rm wobei} \; \, \overline{W} = \overline{A} \cup \overline{D} \cup (\overline{B} \cap C) \cup (B \cap \overline{C}). $$ Für die folgenden Fragen ist zu berücksichtigen, dass $Z = 0 \ ⇒ \ A = B = C = D = 0$ bereits durch den Zahlengenerator ausgeschlossen ist. Beachten Sie ferner, dass nicht alle Eingangsgrößen $A$, $B$, $C$ und $D$ zur Berechnung aller Zwischengrößen $U$, $V$ und $W$ herangezogen werden.

Hinweise:

• Die Aufgabe gehört zum Kapitel Mengentheoretische Grundlagen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:

Mengentheoretische Begriffe und Gesetzmäßigkeiten

Fragebogen zu "A1.2 Schaltlogik (D/B-Wandler)"

1

Welche Aussagen sind bezüglich der Zufallsgröße $U$ zutreffend?

	$U$ beinhaltet 2 Elemente.
	$U$ beinhaltet 4 Elemente.
	Das kleinste Element von $U$ ist 4.
	Das größte Element von $U$ ist 14.

2

Welche Aussagen sind bezüglich der Zufallsgröße $V$ zutreffend?

	$V$ beinhaltet 2 Elemente.
	$V$ beinhaltet 4 Elemente.
	Das kleinste Element von $V$ ist 4.
	Das größte Element von $V$ ist 14.

3

Welche Aussagen sind bezüglich der Zufallsgröße $W$ zutreffend?

	$W$ beinhaltet 2 Elemente.
	$W$ beinhaltet 4 Elemente.
	Das kleinste Element von $W$ ist 4.
	Das größte Element von $W$ ist 14.

4

Welche Aussagen sind bezüglich der Zufallsgröße $P$ zutreffend?

	$P$ beinhaltet alle Zweierpotenzen.
	$P$ beinhaltet alle Primzahlen.
	$P$ beschreibt die leere Menge \(\phi\) .
	$P$ ist identisch mit der Grundmenge $G = {1,2, ... , 15}$.

Musterlösung

Musterlösung

(1)  Das Ereignis $U$ beinhaltet alle diejenigen Zahlen größer/gleich 8 $(A = 1)$, die gerade sind $(D = 0)$: $8, 10, 12, 14$   ⇒   Richtig sind die Lösungsalternativen 2 und 4.

(2)  Das Ereignis $V$ besteht aus den beiden Zahlen $4$ (binär 0100) und $6$ (binär 0110)   ⇒   Richtig sind hier die Lösungsalternativen 1 und 3.

(3)  Für das Ereignis $W$ gilt mit dem Theorem von de Morgan:

$$\overline W = \overline A \cup \overline D \cup (\overline B \cap C) \cup (B \cap \overline C) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W = \overline{\overline W} = A \cap D \cap (\overline{\overline B \cap C}) \cap (\overline{B \cap \overline C}).$$

Mit den Sätzen von de Morgan folgt daraus weiter:

$$ W = A \cap D \cap (B \cup \overline C) \cap (\overline B \cup C).$$

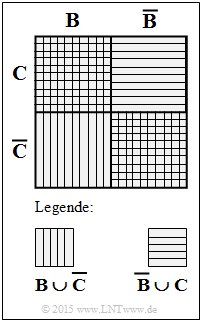
Mit der Boolschen Beziehung $(B \cup \overline C) \cap (\overline B \cup C) = (B \cap C) \cup (\overline B \cap \overline C)$ erhält man schließlich (siehe Skizze):

$W = (A \cap B \cap C \cap D) \cup (A \cap \overline B \cap \overline C \cap D)$.

Somit beinhaltet W die Zahlen $15$ und $9$   ⇒   nur Lösungsvorschlag 1.

(4)  Die Vereinigungsmenge von $U$, $V$ und $W$ beinhaltet folgende Zahlen: $4, 6, 8, 9, 10, 12, 14, 15$. Dementsprechend gilt für die Menge $P$ als das Komplement dieser Vereinigungsmenge:   $P \in {\{1, 2, 3, 5, 7, 11, 13\}}$.

Dies sind genau die mit 4 Bit darstellbaren Primzahlen   ⇒   Lösungsvorschlag 2.