Aufgaben:Aufgabe 2.6: PN-Generator der Länge 5

• Zurück zum Buch

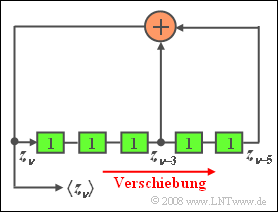
In der Grafik sehen Sie einen Pseudozufallsgenerator der Länge L = 5, der zur Erzeugung einer Binärfolge 〈z_ν〉 eingesetzt werden soll.

Zum Startzeitpunkt seien alle Speicherzellen mit Einsen vorbelegt. Zu jedem Taktzeitpunkt wird der Inhalt des Schieberegisters um eine Stelle nach rechts verschoben und der aktuell erzeugte Binärwert z_ν (0 oder 1) in die erste Speicherzelle eingetragen. Hierbei ergibt sich z_ν aus der Modulo-2-Addition zwischen z_ν–3 und z_ν–5.

Hinweis: Die Aufgabe bezieht sich auf Lehrstoff von Kapitel 2.5. Wir möchten Sie gerne auch auf das folgende Lernvideo hinweisen:

Fragebogen

1

Wie lautet das Generatorpolynom G(D) des dargestellten PN-Generators?

	D5 + D2 + 1.
	D5 + D3 + 1.
	D4 + D2 + D1.

2

Welche Oktalkennung O_G hat dieser PN-Generator?

$O_G$ = (oktal)

3

Gehen Sie davon aus, dass das Generatorpolynom G(D) primitiv ist. Ist die Ausgangsfolge 〈z_ν〉 eine M-Sequenz? Wie groß ist deren Periodendauer P?

$P$ =

4

Welche Oktalkennung O_R beschreibt das reziproke Polynom G_R(D)?

$O_R$ = (oktal)

5

Welche Aussagen gelten für die Konfiguration mit dem Polynom G_R(D)?

	Es handelt sich ebenfalls um eine Folge maximaler Länge.
	Die Ausgangsfolge von GR(D) ist die gleiche wie mit G(D).
	GR(D)– und G(D)–Ausgangsfolgen
	Beide Folgen zeigen gleiche statistische Eigenschaften.
	Bei GR(D) können alle Speicher mit Nullen vorbelegt sein.

Musterlösung

Musterlösung

1.  Richtig ist D⁵ + D³ + 1  ⇒ Lösungsvorschlag 2. Das Generatorpolynom G(D) kennzeichnet die Rückführungen, die zur Modulo-2-Addition herangezogen werden. D ist ein formaler Parameter, der eine Verzögerung um einen Takt angibt. D³ kennzeichnet dann eine Verzögerung um drei Takte.

2.  Es ist g₀ = g₃ = g₅ = 1; alle anderen Rückführungskoeffizienten sind 0. Daraus folgt:

$$(g_{\rm 5}\hspace{0.1cm}g_{\rm 4}\hspace{0.1cm}g_{\rm 3}\hspace{0.1cm}g_{\rm 2}\hspace{0.1cm}g_{\rm 1}\hspace{0.1cm}g_{\rm 0})=\rm (101001)_{bin}\hspace{0.15cm} \underline{=(51)_{oct}}.$$

3.  Da das Generatorpolynom G(D) primitiv ist, erhält man eine M-Sequenz. Dementsprechend ist die Periodendauer maximal: P = 2^L - 1 = 31. Im Theorieteil ist in der Tabelle mit den PN-Generatoren maximaler Länge (M-Sequenzen) für den Grad 5 die Konfiguration (51)_oct aufgeführt.

4.  Das reziproke Polynom lautet:

$$\it G_R(\it D)=\it D^{\rm 5}\cdot(\it D^{\rm -5}+\it D^{\rm -3}+\rm 1)=\it D^{\rm 5}+\it D^{\rm 2}+\rm 1.$$

Somit ist die Oktalkennung für diese Konfiguration (100101)_bin = (45)_oct.

5.  Die Ausgangsfolge der reziproken Realisierung G_R(D) eines primitiven Polynoms G(D) ist immer ebenfalls eine M-Sequenz. Beide Folgen sind zueinander invers.

Das bedeutet: Die Ausgangsfolge von (45)_oct ist gleich der Folge von (51)_oct, wenn man diese von rechts nach links liest und eine Phase (zyklische Verschiebung) berücksichtigt. Voraussetzung ist wieder, dass nicht alle Speicherzellen mit Nullen vorbelegt sind. Unter dieser Bedingung weisen beide Folgen tatsächlich auch gleiche statistische Eigenschaften auf.

Richtig sind somit die Lösungsvorschläge 1, 3 und 4.