Aufgaben:Aufgabe 5.5Z: Rechenaufwand für die FFT: Unterschied zwischen den Versionen
Aus LNTwww
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Signaldarstellung/Fast-Fouriertransformation (FFT) }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Fr…“) |
Khalil (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right | + | [[Datei:P_ID1179__Sig_Z_5_5.png|right]] |
| + | Der FFT–Algorithmus realisiert eine Diskrete Fouriertransformation mit dem kleinstmöglichen Rechenaufwand, wenn der Parameter '''N''' eine Zweierpotenz ist. Im einzelnen sind zur Durchführung einer FFT folgende Rechenschritte notwendig: | ||
| + | :*Die FFT geschieht in ld ''N'' Stufen, wobei in jeder Stufe die genau gleiche Anzahl an Rechenoperationen durchzuführen ist. „ld” steht hier als Abkürzung für den Logarithmus zur Basis 2. | ||
| + | :*Die Grafik zeigt die dritte und letzte Stufe für das Beispiel ''N'' = 8. Man erkennt, dass in dieser und auch den anderen Stufen jeweils ''N''/2 Basisoperationen durchzuführen sind. | ||
| + | |||
| + | :*In jeder Basisoperation, die man häufig auch als '''Butterfly''' bezeichnet, werden aus den beiden komplexen Eingangsgrößen $E_1$ und $E_2$ zwei komplexe Ausgänge berechnet: | ||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 17. März 2017, 11:25 Uhr
Der FFT–Algorithmus realisiert eine Diskrete Fouriertransformation mit dem kleinstmöglichen Rechenaufwand, wenn der Parameter N eine Zweierpotenz ist. Im einzelnen sind zur Durchführung einer FFT folgende Rechenschritte notwendig:
- Die FFT geschieht in ld N Stufen, wobei in jeder Stufe die genau gleiche Anzahl an Rechenoperationen durchzuführen ist. „ld” steht hier als Abkürzung für den Logarithmus zur Basis 2.
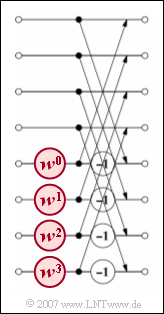
- Die Grafik zeigt die dritte und letzte Stufe für das Beispiel N = 8. Man erkennt, dass in dieser und auch den anderen Stufen jeweils N/2 Basisoperationen durchzuführen sind.
- In jeder Basisoperation, die man häufig auch als Butterfly bezeichnet, werden aus den beiden komplexen Eingangsgrößen $E_1$ und $E_2$ zwei komplexe Ausgänge berechnet:
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.