Aufgaben:Aufgabe 4.3: Algebraische und Modulo-Summe: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Zweidimensionale Zufallsgrößen }} right| :Ein „getakteter”…“) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID253__Sto_A_4_3.png|right|]] | + | [[Datei:P_ID253__Sto_A_4_3.png|right|Algebraische und Modulo-2-Summe]] |
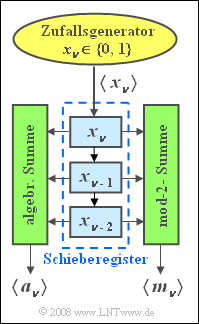
| − | + | Ein „getakteter” Zufallsgenerator liefert eine Folge 〈<i>x<sub>ν</sub></i>〉 von binären Zufallszahlen. Es wird nun vorausgesetzt, dass die Binärzahlen 0 und 1 mit gleichen Wahrscheinlichkeiten auftreten und dass die einzelnen Zufallszahlen nicht statistisch voneinander abhängen. Die Zufallszahlen <i>x<sub>ν</sub></i> ∈ {0, 1} werden in die erste Speicherstelle eines Schieberegisters eingetragen und mit jeden Takt um eine Stelle nach unten verschoben. | |
:Aus den Inhalten des dreistelligen Schieberegisters werden zwei neue Zufallsfolgen 〈<i>a<sub>ν</sub></i>〉 und 〈<i>m<sub>ν</sub></i>〉 gebildet. Hierbei bezeichnet: | :Aus den Inhalten des dreistelligen Schieberegisters werden zwei neue Zufallsfolgen 〈<i>a<sub>ν</sub></i>〉 und 〈<i>m<sub>ν</sub></i>〉 gebildet. Hierbei bezeichnet: | ||
| Zeile 15: | Zeile 15: | ||
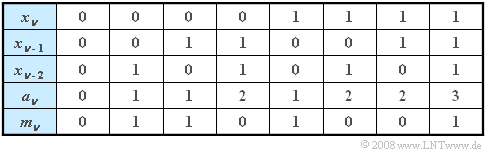
:Dieser Sachverhalt ist in der nachfolgenden Tabelle nochmals dargestellt: | :Dieser Sachverhalt ist in der nachfolgenden Tabelle nochmals dargestellt: | ||
| − | [[Datei:P_ID254__Sto_A_4_3Tab.png|mitte|]] | + | [[Datei:P_ID254__Sto_A_4_3Tab.png|mitte|Tabelle zur Momentenberechnung]] |
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen|Zweidimensionale Zufallsgrößen]]. | ||
| + | *Bezug genommen wird auch auf das Kapitel [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente|Erwartungswerte und Momente]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Berücksichtigen Sie, dass im betrachteten Bereich von $-1 ≤ x ≤ +1$ die Exponentialfunktion wie folgt angenähert werden kann: | ||
| + | :$$y={\rm e}^{x}\approx 1+ \frac{ x}{1!} + \frac{{ x}^{\rm 2}}{\rm 2!}+ \frac{{x}^{\rm 3}}{\rm 3!}+ \frac{{x}^{\rm 4}}{\rm 4!}.$$ | ||
:<b>Hinweis</b>: Die Aufgabe bezieht sich auf den Inhalt von Kapitel 4.1. | :<b>Hinweis</b>: Die Aufgabe bezieht sich auf den Inhalt von Kapitel 4.1. | ||
Version vom 18. März 2017, 17:40 Uhr
Ein „getakteter” Zufallsgenerator liefert eine Folge 〈xν〉 von binären Zufallszahlen. Es wird nun vorausgesetzt, dass die Binärzahlen 0 und 1 mit gleichen Wahrscheinlichkeiten auftreten und dass die einzelnen Zufallszahlen nicht statistisch voneinander abhängen. Die Zufallszahlen xν ∈ {0, 1} werden in die erste Speicherstelle eines Schieberegisters eingetragen und mit jeden Takt um eine Stelle nach unten verschoben.
- Aus den Inhalten des dreistelligen Schieberegisters werden zwei neue Zufallsfolgen 〈aν〉 und 〈mν〉 gebildet. Hierbei bezeichnet:
- aν die algebraische Summe:
- $$a_\nu=x_\nu+x_{\nu-1}+x_{\nu-2},$$
- mν die Modulo–2-Summe:
- $$m_\nu=x_\nu\oplus x_{\nu-1}\oplus x_{\nu-2}.$$
- Dieser Sachverhalt ist in der nachfolgenden Tabelle nochmals dargestellt:
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Zufallsgrößen.
- Bezug genommen wird auch auf das Kapitel Erwartungswerte und Momente.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Berücksichtigen Sie, dass im betrachteten Bereich von $-1 ≤ x ≤ +1$ die Exponentialfunktion wie folgt angenähert werden kann:
- $$y={\rm e}^{x}\approx 1+ \frac{ x}{1!} + \frac{{ x}^{\rm 2}}{\rm 2!}+ \frac{{x}^{\rm 3}}{\rm 3!}+ \frac{{x}^{\rm 4}}{\rm 4!}.$$
- Hinweis: Die Aufgabe bezieht sich auf den Inhalt von Kapitel 4.1.
Fragebogen
Musterlösung
- 1. Aus der Tabelle auf der Angabenseite ist ersichtlich, dass bei der Modulo-2-Summe die beiden Werte 0 und 1 mit gleicher Wahrscheinlichkeit (also jeweils 0.5) auftreten.
- 2. Die Tabelle zeigt, dass bei jeder Vorbelegung, - das heißt (xν–1, xν–2) = (0,0), (0,1), (1,0), (1,1) - die Werte mν = 0 bzw. mν = 1 mit gleicher Wahrscheinlichkeit auftreten. Anders ausgedrückt:
- $$\rm Pr(\it m_{\nu}|m_{\nu-\rm 1}) = \rm Pr(\it m_{\nu}).$$
- Dies entspricht genau der Definition der statistischen Unabhängigkeit.
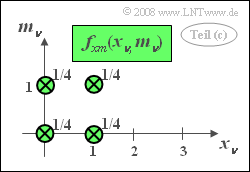
- 3. Die 2D–WDF besteht aus vier Diracfunktionen, jeweils mit dem Gewicht 1/4. Man erhält dieses Ergebnis beispielsweise durch Auswertung der Tabelle auf der Angabenseite.
- Da fxm(xν, mν) gleich dem Produkt fx(xν) · fm(mν) ist, sind die Größen xν und mν statistisch unabhängig. Statistisch unabhängige Zufallsgrößen sind aber natürlich auch linear statistisch unabhängig, also mit Sicherheit unkorreliert. Richtig sind also der zweite und der letzte Lösungsvorschlag.
- 4. Innerhalb der Folge 〈aν〉 der algebraischen Summe gibt es statistische Bindungen ⇒ Vorschlag 2. Man erkennt dies daran, dass die unbedingte Wahrscheinlichkeit Pr(aν = 0) = 1/8 ist, während zum Beispiel Pr(aν = 0 | aν–1 = 3) gleich 0 ist.
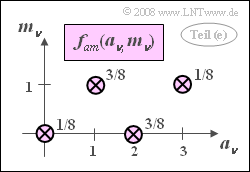
- 5. Wie bei der Teilaufgabe (3) erhält man wieder vier Diracfunktionen, diesmal aber nicht mit jeweils gleichem Impulsgewicht 1/4.
- Die zweidimensionale WDF lässt sich nicht als Produkt der zwei Randwahrscheinlichkeitsdichten schreiben. Das bedeutet aber, dass statistische Bindungen zwischen aν und mν bestehen müssen.
- Für den gemeinsamen Erwartungswert erhält man:
- $$\rm E[\it a\cdot \it m] = \rm \frac{1}{8}\cdot 0 \cdot 0 +\frac{3}{8}\cdot 2 \cdot 0 +\frac{3}{8}\cdot 1 \cdot 1 + \frac{1}{8}\cdot 3 \cdot 1 = \frac{3}{4}.$$
- Mit den linearen Mittelwerten E[a] = 1.5 und E[m] = 0.5 folgt damit für die Kovarianz:
- $$\mu_{am}= \rm E[\it a\cdot m] - \rm E[\it a]\cdot \rm E[\it m] = \rm 0.75-1.5\cdot 0.5 = \rm 0.$$
- Damit ist auch der Korrelationskoeffizient ρam = 0. Das heißt: Die vorhandenen Abhängigkeiten sind nichtlinear. Die Größen aν und mν sind zwar statistisch abhängig, aber trotzdem unkorreliert. Richtig sind der erste und der letzte Lösungsvorschlag.