Aufgaben:4.1:WDF, VTF und Wahrscheinlichkeit: Unterschied zwischen den Versionen
Khalil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/Differentielle Entropie }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |ty…“) |
Khalil (Diskussion | Beiträge) |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID2862__Inf_A_4_1_neu.png|right|]] |
| + | Zur Wiederholung einiger wichtiger Grundlagen aus dem Buch [http://www.lntwww.de/Stochastische_Signaltheorie '''stochastischen Signaltheorie'''] | ||
| + | beschäftigen wir uns mit | ||
| + | :* der [http://www.lntwww.de/Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion '''Wahrscheinlichkeitsdichtefunktion '''] (WDF), | ||
| + | :* der [http://www.lntwww.de/Stochastische_Signaltheorie/Verteilungsfunktion ''' Verteilungsfunktion '''] (VTF). | ||
| + | Die obere Darstellung zeigt die Verteilungsfunktion $F_X(x)$ einer wertdiskreten Zufallsgröße ''X''. Die zugehörige WDF $f_X(x)$ ist in der Teilaufgabe (a) zu bestimmen. Die Gleichung | ||
| + | $$ {\rm Pr}(A < X \le B) \hspace{-0.15cm} = \hspace{-0.15cm} F_X(B) - F_X(A) = $$ | ||
| + | $$ =\hspace{-0.15cm} \lim_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm}0} \int\limits_{A+\varepsilon}^{B+\varepsilon} \hspace{-0.15cm} f_X(x) \hspace{0.1cm}{\rm d}x $$ | ||
| + | stellt zwei Möglichkeiten dar, um die Wahrscheinlichkeit für das Ereignis „Die Zufallsgröße ''X'' liegt in einem Intervall” aus der VTF bzw. der WDF zu berechnen. | ||
| + | |||
| + | Die untere Grafik zeigt die Wahrscheinlichkeitsdichtefunktion | ||
| + | $$ f_Y(y) = \left\{ \begin{array}{c} \hspace{0.1cm}1/2 \cdot \cos^2(\pi/4 \cdot y) \\ \hspace{0.1cm} 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}l} | y| \le 2, \\ | ||
| + | y < -2 \hspace{0.1cm}{\rm und}\hspace{0.1cm}y > +2 \\ \end{array}$$ | ||
| + | einer wertkontinuierlichen Zufallsgröße Y, die auf den Bereich |''Y''| ≤ 2 begrenzt ist. | ||
| + | |||
| + | Prinzipiell besteht bei der kontinuierlichen Zufallsgröße ''Y'' der gleiche Zusammenhang zwischen WDF, VTF und Wahrscheinlichkeiten wie bei einer diskreten Zufallsgröße. Sie werden trotzdem einige Detailunterschiede feststellen. Beispielsweise kann bei der kontinuierlichen Zufallsgröße ''Y'' in obiger Gleichung auf den Grenzübergang verzichtet werden, und man erhält vereinfacht: | ||
| + | $${\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A) =\int_{A}^{B} \hspace{-0.01cm} f_Y(y) | ||
| + | \hspace{0.1cm}{\rm d}y\hspace{0.05cm}$$. | ||
| + | |||
| + | '''Hinweis''': Die Aufgabe dient zur Vorbereitung der in [http://www.lntwww.de/Informationstheorie/Differentielle_Entropie '''Kapitel 4.1'''] dargelegten Thematik. Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im [http://www.lntwww.de/Stochastische_Signaltheorie '''Kapitel 3'''] des Buches „Stochastische Signaltheorie”. | ||
| + | Gegeben ist zudem das folgende unbstimmte Integral: | ||
| + | $$\int \hspace{0.1cm} \cos^2(A \eta) \hspace{0.1cm}{\rm d}\eta = \frac{\eta}{2} + \frac{1}{4A} \cdot \sin(2A \eta)$$. | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Bestimmen Sie die WDF <i>f<sub>X</sub></i>(<i>x</i>) der wertdiskreten Zufallsgröße <i>X</i>. Welche der folgenden Aussagen sind zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | - | + | + Die WDF setzt sich aus fünf Diracfunktionen zusammen. |
| − | + | + Es gilt Pr(<i>X</i> = 0) = 0.4 und Pr(<i>X</i> = 1) = 0.2. | |
| + | - Es gilt Pr(<i>X</i> = 2) = 0.4. | ||
| + | |||
| + | |||
| + | {Berechnen Sie die folgenden Wahrscheinlichkeiten: | ||
| + | |type="{}"} | ||
| + | $Pr(X > 0)$ = { 0.3 3% } | ||
| + | $Pr(|X| ≤ 1)$ = { 0.8 3% } | ||
| + | {Welche Werte ergeben sich für die Verteilungsfunktion <i>F<sub>Y</sub></i>(<i>y</i>) = Pr(<i>Y</i> ≤ <i>y</i>) der wertkontinuierlichen Zufallsgröße <i>Y</i>, insbesondere: | ||
| + | |type="{}"} | ||
| + | $F_Y(y = 0)$ = { 0.5 3% } | ||
| + | $F_Y(y = 1)$ = { 1 3% } | ||
| + | $F_Y(y = 2)$ = { 0.909 3% } | ||
| − | { | + | {Wie groß ist die Wahrscheinlichkeit, dass <i>Y</i> = 0 ist? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $Pr(Y = 0)$ = { 0 3% } |
| + | {Welche der folgenden Aussagen sind richtig? | ||
| + | |type="[]"} | ||
| + | - Das Ergebnis <i>Y</i> = 0 ist unmöglich. | ||
| + | + Das Ergebnis <i>Y</i> = 3 ist unmöglich. | ||
| + | {Wie groß sind die folgenden Wahrscheinlichkeiten? | ||
| + | |type="{}"} | ||
| + | $Pr(Y > 0)$ = { 0.5 3% } | ||
| + | $Pr(|Y| ≤ 1)$ = { 0.818 3% } | ||
</quiz> | </quiz> | ||
| Zeile 25: | Zeile 66: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | [[Datei:P_ID2857__Inf_A_4_1a_neu.png|right|]] | |
| − | + | <b>a)</b> Die Verteilungsfunktion (VTF) <i>F<sub>X</sub></i>(<i>x</i>) ergibt sich aus der Wahrscheinlichkeitsdichtefunktion <i>f<sub>X</sub></i>(<i>x</i>) durch Integration über die (umbenannte) Zufallsgröße im Bereich von –∞ bis <i>x</i>. Die Umkehrung lautet: Ist die VTF gegeben, so erhält man die WDF durch Differentiation. | |
| − | + | Die vorgegebene VTF beinhaltet fünf Unstetigkeitsstellen, die nach der Differentiation zu fünf Diracfunktionen führen: | |
| − | + | $$f_X(x) \hspace{-0.15cm} = \hspace{-0.15cm} 0.1 \cdot {\rm \delta}( x+2) | |
| − | + | + 0.2 \cdot {\rm \delta}( x+1) $$ $$\ | |
| − | + | + \hspace{-0.15cm} 0.4 \cdot {\rm \delta}( x) + 0.2 \cdot {\rm \delta}( x-1) $$ $$\ | |
| − | + | +\hspace{-0.15cm} 0.1 \cdot {\rm \delta}( x-2)\hspace{0.05cm}.$$ | |
| + | Die Diracgewichte geben die Auftrittswahrscheinlichkeiten der Zufallsgröße <i>X</i> = {–2, –1, 0, +1, +2} an, zum Beispiel: | ||
| + | $${\rm Pr}(X = 0) \hspace{-0.15cm} = \hspace{-0.15cm} F_X(x \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{+}) - F_X(x \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{-})$$ $$=\ | ||
| + | \hspace{-0.15cm} 0.7 - 0.3 = 0.4\hspace{0.05cm}.$$ | ||
| + | Dementsprechend lauten die weiteren Wahrscheinlichkeiten: | ||
| + | $${\rm Pr}(X = +1) = {\rm Pr}(X = -1) = 0.2\hspace{0.05cm},\hspace{0.3cm} | ||
| + | {\rm Pr}(X = +2) = {\rm Pr}(X = -2) = 0.1\hspace{0.05cm}.$$ | ||
| + | Richtig sind somit die <u>Lösungsvorschläge 1 und 2</u>. | ||
| + | |||
| + | <b>b)</b> Aus der eben berechneten WDF erhält man: | ||
| + | $${\rm Pr}(X >0) \hspace{-0.15cm} = \hspace{-0.15cm} {\rm Pr}(X = +1) + {\rm Pr}(X = +2) | ||
| + | \hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$ $$\ | ||
| + | {\rm Pr}(|X| \le 1) \hspace{-0.15cm} = \hspace{-0.15cm} | ||
| + | {\rm Pr}(X = -1) + {\rm Pr}(X = 0) + {\rm Pr}(X = +1) = 0.2 + 0.4 +0.2 | ||
| + | \hspace{0.15cm}\underline {= 0.8}\hspace{0.05cm}.$$ | ||
| + | |||
| + | Zum gleichen Ergebnis kommt man über die Verteilungsfunktion. Hier lautet die allgemeine Gleichung, die für wertdiskrete und wertkontinuierliche Zufallsgrößen gleichermaßen gilt: | ||
| + | $${\rm Pr}(A < X \le B) =F_X(B) - F_X(A) \hspace{0.05cm}.$$ | ||
| + | |||
| + | :* Mit <i>A</i> = 0 und <i>B</i> = +2 erhält man somit: | ||
| + | $${\rm Pr}(0 < X \le +2) = {\rm Pr}(X >0)= F_X(+2) - F_X(0) = 1 - 0.7 \hspace{0.15cm}\underline {= 0.3} \hspace{0.05cm}.$$ | ||
| + | :*Setzt man A = –2 und B = +1, so ergibt sich: | ||
| + | $${\rm Pr}(-2 < X \le +1) = {\rm Pr}(|X| \le 1)= F_X(+1) - F_X(-2) = 0.9 - 0.1 \hspace{0.15cm}\underline {= 0.8} \hspace{0.05cm}.$$ | ||
| + | |||
| + | <b>c)</b> Die Verteilungsfunktion <i>F<sub>Y</sub></i>(<i>y</i>) ergibt sich aus der (umbenannten) WDF <i>f<sub>Y</sub></i>(<i>η</i>) durch Integration von <nobr>–∞ bis <i>y</i></nobr>. Aufgrund der Symmetrie kann hierfür im Bereich 0 ≤ <i>y</i> ≤ 2 geschrieben werden: | ||
| + | $$F_Y(y) = \int_{-\infty}^{\hspace{0.05cm}y} \hspace{-0.1cm}f_Y(\eta) \hspace{0.1cm}{\rm d}\eta =\frac{1}{2}+\int_{0}^{\hspace{0.05cm}y} \hspace{-0.1cm}f_Y(\eta) \hspace{0.1cm}{\rm d}\eta.$$ | ||
| + | $$\Rightarrow \hspace{0.3cm}F_Y(y) = \frac{1}{2}+\int_{0}^{\hspace{0.05cm}y} \hspace{0.1cm}\frac{1}{2} \cdot \cos^2(\frac{\pi}{4} \cdot \eta) \hspace{0.1cm}{\rm d}\eta = \frac{1}{2}+\frac{y}{4} + \frac{1}{2\pi} \cdot \sin(\frac{\pi}{2} \cdot y).$$ | ||
| + | [[Datei:P_ID2858__Inf_A_4_1c_neu.png|right|]] | ||
| + | Die Gleichung gilt im gesamten Bereich –2 ≤ <i>y</i> ≤ +2. Die gesuchten VTF–Werte sind damit: | ||
| + | :*<i>F<sub>Y</sub></i>(<i>y</i> = 0)<u> = 0.5</u> (Integral über die halbe WDF) | ||
| + | :*<i>F<sub>Y</sub></i>(<i>y</i> = 2)<u> = 1</u> (Integral über die gesamte WDF) | ||
| + | :*<i>F<sub>Y</sub></i>(<i>y</i><u> = 1)</u> = 3/4 + 1/(2 <i>π</i>) <u>≈ 0.909</u> (rot hinterlegte Fläche in der WDF) | ||
| + | |||
| + | <br><b>d)</b> Die Wahrscheinlichkeit, dass die wertkontinuierliche Zufallsgröße <i>Y</i> im Bereich von –<i>ε</i> bis +<i>ε</i> liegt, kann mit der angegebenen Gleichung wie folgt berechnet werden: | ||
| + | $${\rm Pr}(-\varepsilon \le Y \le +\varepsilon) = F_Y(+\varepsilon) - F_Y(-\varepsilon) \hspace{0.05cm}.$$ | ||
| + | |||
| + | Berücksichtigt wurde, dass man bei der kontinuierlichen Zufallsgröße <i>Y</i> das „<”–Zeichen ohne Verfälschung durch das „≤”–Zeichen ersetzen kann. Mit dem Grenzübergang <i>ε</i> → 0 ergibt sich die gesuchte Wahrscheinlichkeit: | ||
| + | $${\rm Pr}(Y = 0) \hspace{-0.15cm} = \hspace{-0.15cm} \ lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm}{\rm Pr}(-\varepsilon \le Y \le +\varepsilon) = | ||
| + | \lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm} F_Y(+\varepsilon) - \lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm} F_Y(-\varepsilon)$$ $$=\ | ||
| + | \hspace{-0.15cm} F_Y(y \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{+}) - F_Y(y \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{-})\hspace{0.05cm}.$$ | ||
| + | |||
| + | Da bei einer kontinuierlichen Zufallsgröße die beiden Grenzwerte gleich sind, gilt <u>Pr(<i>Y</i> = 0) = 0</u>. | ||
| + | |||
| + | <u>Allgemein gilt:</u> Die Wahrscheinlichkeit Pr(<i>Y</i> = <i>y</i><sub>0</sub>), dass eine wertkontinuierliche Zufallsgröße <i>Y</i> einen festen Wert <i>y</i><sub>0</sub> annimmt, ist stets 0. | ||
| + | |||
| + | <b>e)</b> Richtig ist der <u>Lösungsvorschlag 2</u>: Aufgrund der vorliegenden WDF kann das Ergebnis <i>Y</i> = 3 ausgeschlossen werden. Das Ergebnis <i>Y</i> = 0 ist dagegen durchaus möglich, obwohl Pr(<i>Y</i> = 0) = 0 ist. Führt man zum Beispiel ein Zufallsexperiment <i>N</i> → ∞ mal durch und erhält dabei <i>N</i><sub>0</sub> mal das Ergebnis <i>Y</i> = 0, so gilt bei endlichem <i>N</i><sub>0</sub> nach der klassischen Definition: | ||
| + | $${\rm Pr}(Y = 0) = \lim_{N\hspace{0.05cm}\rightarrow\hspace{0.05cm}\infty}\hspace{0.1cm}{N_0}/{N} = 0\hspace{0.05cm}.$$ | ||
| + | |||
| + | <b>f)</b> Wir gehen wieder von der Gleichung Pr(<i>A</i> ≤ <i>Y</i> ≤ <i>B</i>) = <i>F<sub>Y</sub></i>(<i>B</i>) – <i>F<sub>Y</Sub></i>(<i>A</i>) aus. Mit <i>A</i> = 0 und <i>B</i> → ∞ (bzw. <i>B</i> = 2) erhält man: | ||
| + | $${\rm Pr}( Y > 0) = {\rm Pr}(0 \le Y \le \infty) | ||
| + | = {\rm Pr}(0 \le Y \le 2) = F_Y(2) - F_Y(0) | ||
| + | \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}.$$ | ||
| + | |||
| + | Bei der symmetrischen kontinuierlichen Zufallsgröße <i>Y</i> ist erwartungsgemäß Pr(<i>Y</i> > 0) = 1/2. Obwohl auch die wertdiskrete Zufallsgröße <i>X</i> symmetrisch um <i>x</i> = 0 ist, wurde dagegen oben Pr(<i>X</i> > 0) = 0.3 ermittelt. Weiter erhält man mit <i>A</i> = –1 und <i>B</i> = +1 wegen <i>F<sub>Y</Sub></i>(–1) = 1 – | ||
| + | <i>F<sub>Y</sub></i>(+1): | ||
| + | |||
| + | $${\rm Pr}( |Y| \le 1) = {\rm Pr}(-1 \le Y \le +1) | ||
| + | = F_Y(+1) - F_Y(-1) $$ $$\ | ||
| + | = 2 \cdot F_Y(+1) -1 = 2 \cdot 0.909 -1 \hspace{0.15cm}\underline {= 0.818}. $$ | ||
| + | |||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben | + | [[Category:Aufgaben zuInformationstheorie|^4.1 Differentielle Entropie^]] |
Aktuelle Version vom 24. März 2017, 18:14 Uhr
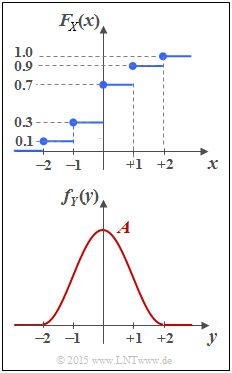
Zur Wiederholung einiger wichtiger Grundlagen aus dem Buch stochastischen Signaltheorie beschäftigen wir uns mit
- der Wahrscheinlichkeitsdichtefunktion (WDF),
- der Verteilungsfunktion (VTF).
Die obere Darstellung zeigt die Verteilungsfunktion $F_X(x)$ einer wertdiskreten Zufallsgröße X. Die zugehörige WDF $f_X(x)$ ist in der Teilaufgabe (a) zu bestimmen. Die Gleichung $$ {\rm Pr}(A < X \le B) \hspace{-0.15cm} = \hspace{-0.15cm} F_X(B) - F_X(A) = $$ $$ =\hspace{-0.15cm} \lim_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm}0} \int\limits_{A+\varepsilon}^{B+\varepsilon} \hspace{-0.15cm} f_X(x) \hspace{0.1cm}{\rm d}x $$
stellt zwei Möglichkeiten dar, um die Wahrscheinlichkeit für das Ereignis „Die Zufallsgröße X liegt in einem Intervall” aus der VTF bzw. der WDF zu berechnen.
Die untere Grafik zeigt die Wahrscheinlichkeitsdichtefunktion $$ f_Y(y) = \left\{ \begin{array}{c} \hspace{0.1cm}1/2 \cdot \cos^2(\pi/4 \cdot y) \\ \hspace{0.1cm} 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}l} | y| \le 2, \\ y < -2 \hspace{0.1cm}{\rm und}\hspace{0.1cm}y > +2 \\ \end{array}$$ einer wertkontinuierlichen Zufallsgröße Y, die auf den Bereich |Y| ≤ 2 begrenzt ist.
Prinzipiell besteht bei der kontinuierlichen Zufallsgröße Y der gleiche Zusammenhang zwischen WDF, VTF und Wahrscheinlichkeiten wie bei einer diskreten Zufallsgröße. Sie werden trotzdem einige Detailunterschiede feststellen. Beispielsweise kann bei der kontinuierlichen Zufallsgröße Y in obiger Gleichung auf den Grenzübergang verzichtet werden, und man erhält vereinfacht: $${\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A) =\int_{A}^{B} \hspace{-0.01cm} f_Y(y) \hspace{0.1cm}{\rm d}y\hspace{0.05cm}$$.
Hinweis: Die Aufgabe dient zur Vorbereitung der in Kapitel 4.1 dargelegten Thematik. Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im Kapitel 3 des Buches „Stochastische Signaltheorie”. Gegeben ist zudem das folgende unbstimmte Integral: $$\int \hspace{0.1cm} \cos^2(A \eta) \hspace{0.1cm}{\rm d}\eta = \frac{\eta}{2} + \frac{1}{4A} \cdot \sin(2A \eta)$$.
Fragebogen
Musterlösung
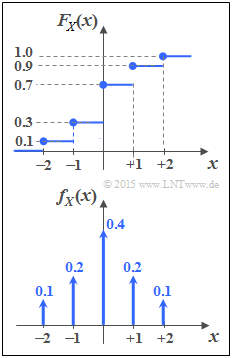
a) Die Verteilungsfunktion (VTF) FX(x) ergibt sich aus der Wahrscheinlichkeitsdichtefunktion fX(x) durch Integration über die (umbenannte) Zufallsgröße im Bereich von –∞ bis x. Die Umkehrung lautet: Ist die VTF gegeben, so erhält man die WDF durch Differentiation. Die vorgegebene VTF beinhaltet fünf Unstetigkeitsstellen, die nach der Differentiation zu fünf Diracfunktionen führen: $$f_X(x) \hspace{-0.15cm} = \hspace{-0.15cm} 0.1 \cdot {\rm \delta}( x+2) + 0.2 \cdot {\rm \delta}( x+1) $$ $$\ + \hspace{-0.15cm} 0.4 \cdot {\rm \delta}( x) + 0.2 \cdot {\rm \delta}( x-1) $$ $$\ +\hspace{-0.15cm} 0.1 \cdot {\rm \delta}( x-2)\hspace{0.05cm}.$$ Die Diracgewichte geben die Auftrittswahrscheinlichkeiten der Zufallsgröße X = {–2, –1, 0, +1, +2} an, zum Beispiel: $${\rm Pr}(X = 0) \hspace{-0.15cm} = \hspace{-0.15cm} F_X(x \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{+}) - F_X(x \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{-})$$ $$=\ \hspace{-0.15cm} 0.7 - 0.3 = 0.4\hspace{0.05cm}.$$ Dementsprechend lauten die weiteren Wahrscheinlichkeiten: $${\rm Pr}(X = +1) = {\rm Pr}(X = -1) = 0.2\hspace{0.05cm},\hspace{0.3cm} {\rm Pr}(X = +2) = {\rm Pr}(X = -2) = 0.1\hspace{0.05cm}.$$ Richtig sind somit die Lösungsvorschläge 1 und 2.
b) Aus der eben berechneten WDF erhält man: $${\rm Pr}(X >0) \hspace{-0.15cm} = \hspace{-0.15cm} {\rm Pr}(X = +1) + {\rm Pr}(X = +2) \hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$ $$\ {\rm Pr}(|X| \le 1) \hspace{-0.15cm} = \hspace{-0.15cm} {\rm Pr}(X = -1) + {\rm Pr}(X = 0) + {\rm Pr}(X = +1) = 0.2 + 0.4 +0.2 \hspace{0.15cm}\underline {= 0.8}\hspace{0.05cm}.$$
Zum gleichen Ergebnis kommt man über die Verteilungsfunktion. Hier lautet die allgemeine Gleichung, die für wertdiskrete und wertkontinuierliche Zufallsgrößen gleichermaßen gilt: $${\rm Pr}(A < X \le B) =F_X(B) - F_X(A) \hspace{0.05cm}.$$
- Mit A = 0 und B = +2 erhält man somit:
$${\rm Pr}(0 < X \le +2) = {\rm Pr}(X >0)= F_X(+2) - F_X(0) = 1 - 0.7 \hspace{0.15cm}\underline {= 0.3} \hspace{0.05cm}.$$
- Setzt man A = –2 und B = +1, so ergibt sich:
$${\rm Pr}(-2 < X \le +1) = {\rm Pr}(|X| \le 1)= F_X(+1) - F_X(-2) = 0.9 - 0.1 \hspace{0.15cm}\underline {= 0.8} \hspace{0.05cm}.$$
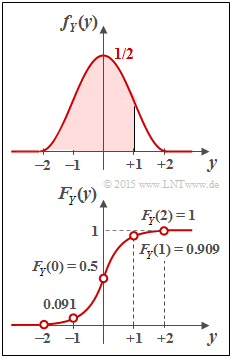
c) Die Verteilungsfunktion FY(y) ergibt sich aus der (umbenannten) WDF fY(η) durch Integration von <nobr>–∞ bis y</nobr>. Aufgrund der Symmetrie kann hierfür im Bereich 0 ≤ y ≤ 2 geschrieben werden: $$F_Y(y) = \int_{-\infty}^{\hspace{0.05cm}y} \hspace{-0.1cm}f_Y(\eta) \hspace{0.1cm}{\rm d}\eta =\frac{1}{2}+\int_{0}^{\hspace{0.05cm}y} \hspace{-0.1cm}f_Y(\eta) \hspace{0.1cm}{\rm d}\eta.$$ $$\Rightarrow \hspace{0.3cm}F_Y(y) = \frac{1}{2}+\int_{0}^{\hspace{0.05cm}y} \hspace{0.1cm}\frac{1}{2} \cdot \cos^2(\frac{\pi}{4} \cdot \eta) \hspace{0.1cm}{\rm d}\eta = \frac{1}{2}+\frac{y}{4} + \frac{1}{2\pi} \cdot \sin(\frac{\pi}{2} \cdot y).$$
Die Gleichung gilt im gesamten Bereich –2 ≤ y ≤ +2. Die gesuchten VTF–Werte sind damit:
- FY(y = 0) = 0.5 (Integral über die halbe WDF)
- FY(y = 2) = 1 (Integral über die gesamte WDF)
- FY(y = 1) = 3/4 + 1/(2 π) ≈ 0.909 (rot hinterlegte Fläche in der WDF)
d) Die Wahrscheinlichkeit, dass die wertkontinuierliche Zufallsgröße Y im Bereich von –ε bis +ε liegt, kann mit der angegebenen Gleichung wie folgt berechnet werden:
$${\rm Pr}(-\varepsilon \le Y \le +\varepsilon) = F_Y(+\varepsilon) - F_Y(-\varepsilon) \hspace{0.05cm}.$$
Berücksichtigt wurde, dass man bei der kontinuierlichen Zufallsgröße Y das „<”–Zeichen ohne Verfälschung durch das „≤”–Zeichen ersetzen kann. Mit dem Grenzübergang ε → 0 ergibt sich die gesuchte Wahrscheinlichkeit: $${\rm Pr}(Y = 0) \hspace{-0.15cm} = \hspace{-0.15cm} \ lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm}{\rm Pr}(-\varepsilon \le Y \le +\varepsilon) = \lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm} F_Y(+\varepsilon) - \lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm} F_Y(-\varepsilon)$$ $$=\ \hspace{-0.15cm} F_Y(y \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{+}) - F_Y(y \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{-})\hspace{0.05cm}.$$
Da bei einer kontinuierlichen Zufallsgröße die beiden Grenzwerte gleich sind, gilt Pr(Y = 0) = 0.
Allgemein gilt: Die Wahrscheinlichkeit Pr(Y = y0), dass eine wertkontinuierliche Zufallsgröße Y einen festen Wert y0 annimmt, ist stets 0.
e) Richtig ist der Lösungsvorschlag 2: Aufgrund der vorliegenden WDF kann das Ergebnis Y = 3 ausgeschlossen werden. Das Ergebnis Y = 0 ist dagegen durchaus möglich, obwohl Pr(Y = 0) = 0 ist. Führt man zum Beispiel ein Zufallsexperiment N → ∞ mal durch und erhält dabei N0 mal das Ergebnis Y = 0, so gilt bei endlichem N0 nach der klassischen Definition: $${\rm Pr}(Y = 0) = \lim_{N\hspace{0.05cm}\rightarrow\hspace{0.05cm}\infty}\hspace{0.1cm}{N_0}/{N} = 0\hspace{0.05cm}.$$
f) Wir gehen wieder von der Gleichung Pr(A ≤ Y ≤ B) = FY(B) – FY(A) aus. Mit A = 0 und B → ∞ (bzw. B = 2) erhält man: $${\rm Pr}( Y > 0) = {\rm Pr}(0 \le Y \le \infty) = {\rm Pr}(0 \le Y \le 2) = F_Y(2) - F_Y(0) \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}.$$
Bei der symmetrischen kontinuierlichen Zufallsgröße Y ist erwartungsgemäß Pr(Y > 0) = 1/2. Obwohl auch die wertdiskrete Zufallsgröße X symmetrisch um x = 0 ist, wurde dagegen oben Pr(X > 0) = 0.3 ermittelt. Weiter erhält man mit A = –1 und B = +1 wegen FY(–1) = 1 – FY(+1):
$${\rm Pr}( |Y| \le 1) = {\rm Pr}(-1 \le Y \le +1) = F_Y(+1) - F_Y(-1) $$ $$\ = 2 \cdot F_Y(+1) -1 = 2 \cdot 0.909 -1 \hspace{0.15cm}\underline {= 0.818}. $$