Aufgaben:Aufgabe 4.13Z: AMI-Code: Unterschied zwischen den Versionen
| Zeile 78: | Zeile 78: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
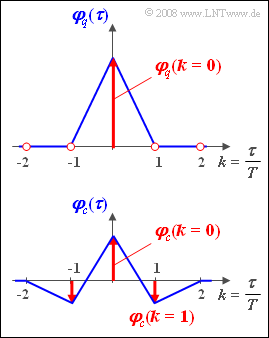
| − | + | '''(1)''' Der diskrete AKF-Wert für $k = 0$ gibt den quadratischen Mittelwert (hier gleich der Varianz) der Quellensymbole an. Da $q_\nu$ nur die Werte $-1$ und $+1$ annehmen kann, ist $\varphi_q(k=0)\hspace{0.15cm}\underline{= 1}$. | |
| − | + | '''(2)''' Richtig sind <u>die Lösungsvorschläge 1 und 3</u>: | |
| + | *Die zeitdiskrete AKF und deren Fouriertransformierte lauten: | ||
:$${\rm A} \{ \varphi_q ( \tau ) \} = \varphi_q ( k = 0) \cdot T \cdot \delta (\tau) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{\it \Phi_q}( f) \} = \varphi_q ( k = 0) \cdot T = T.$$ | :$${\rm A} \{ \varphi_q ( \tau ) \} = \varphi_q ( k = 0) \cdot T \cdot \delta (\tau) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{\it \Phi_q}( f) \} = \varphi_q ( k = 0) \cdot T = T.$$ | ||
| + | *Es ist berücksichtigt, dass $\varphi_q(k=0)\sigma_q^2= 1$ ist. Das bedeutet: Die periodische Fortsetzung von ${\rm P} \{ {\it \Phi}_q(f) \}$ ergibt somit für alle Frequenzen den gleichen Wert. | ||
| + | *Dagegen kann die zeitkontinuierliche AKF wie folgt dargestellt werden: $ \varphi_q ( \tau ) = {\rm A} \{ \varphi_q ( \tau ) \} \star ( {\rm \Delta} ( \tau) / T ).$ | ||
| + | *Das dazugehörige Leistungsdichtespektrum (Fouriertransformierte der AKF) ist dann das Produkt der Fouriertransformierten der beiden Faltungsterme: $ {\it \Phi_q} ( f) = {\rm P} \{ {\it \Phi_q}( f) \} \cdot {\rm si}^2 (\pi f T ) = T \cdot {\rm si}^2 (\pi f T ) .$ | ||
| + | *Aufgrund der gewählten AKF-Interpolation (mit Geradenabschnitten) aus ihren Abtastwerten ergibt sich ein si<sup>2</sup>-förmiges LDS. Ein rechteckförmiges Spektrum (Lösungsvorschlag 2) würde sich nur bei si-förmiger Interpolation einstellen. | ||
| − | |||
| − | : | + | '''(3)''' Die codierte Folge lautet: $\langle +1, 0, -1, +1, 0, -1, +1, 0, 0, 0 \rangle$. Das 6. Symbol ist somit $c_6\hspace{0.15cm}\underline{= -1}$. |
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' Die Auftrittswahrscheinlichkeiten der Werte $-1$, $0$ und $+1$ sind $0.25, 0.5, 0.25$. Daraus folgt: | |
| − | |||
| − | |||
| − | |||
| − | |||
:$$\varphi_c ( k = 0) = 0.25 \cdot (-1)^2 + 0.5 \cdot 0^2 +0.25 \cdot (+1)^2\hspace{0.15cm}\underline{ = 0.5}. $$ | :$$\varphi_c ( k = 0) = 0.25 \cdot (-1)^2 + 0.5 \cdot 0^2 +0.25 \cdot (+1)^2\hspace{0.15cm}\underline{ = 0.5}. $$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
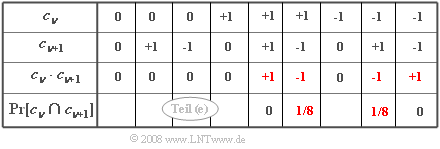
| − | :Hierbei ist vorausgesetzt, dass | + | '''(5)''' Für den AKF-Wert bei $k = 1$ betrachtet man das Produkt $c_{\nu} \cdot c_{\nu+1}$. Es ergeben sich die rechts gezeigten Kombinationen. Einen Beitrag liefern nur Produkte $c_{\nu} \cdot c_{\nu+1} \ne 0$ mit ${\rm}[c_{\nu} \cdot c_{\nu+1}] \ne 0$: |
| + | :$$\varphi_c ( k = 1) = {\rm Pr} \left [( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \right ] \cdot (+1) \cdot (-1) + {\rm Pr} \left [ ( c_{\nu} = -1) \cap ( c_{\nu + 1} = +1) \right ] \cdot (-1) \cdot (+1).$$ | ||
| + | [[Datei:P_ID428__Sto_Z_4_13_e.png|right|framed|Zur AKF-Berechnung des AMI-Codes]] | ||
| + | In der Tabelle sind diese Terme rot gekennzeichnet. Weiter gilt: | ||
| + | :$$ {\rm Pr} \left [ ( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \right ] = $$ | ||
| + | :$$ = {\rm Pr} ( c_{\nu} = +1) \cdot {\rm Pr} \left ( c_{\nu + 1} = -1 | c_{\nu } = +1) \right ) = \frac{1}{4} \cdot \frac{1}{2}= \frac{1}{8} . $$ | ||
| + | Hierbei ist vorausgesetzt, dass $+1$ mit der Wahrscheinlichkeit $0.25$ auftritt und danach $-1$ nur in der Hälfte der Fälle folgt. Das gleiche Ergebnis erhält man für den zweiten Beitrag. Damit gilt: | ||
:$$\varphi_c ( k = 1) = \frac {1}{8} \cdot (+1)\cdot (-1) + \frac {1}{8} \cdot (-1)\cdot (+1) \hspace{0.15cm}\underline{= -0.25}.$$ | :$$\varphi_c ( k = 1) = \frac {1}{8} \cdot (+1)\cdot (-1) + \frac {1}{8} \cdot (-1)\cdot (+1) \hspace{0.15cm}\underline{= -0.25}.$$ | ||
| + | :$$\varphi_c ( k = -1) = \varphi_c ( k = 1) \hspace{0.15cm}\underline{= -0.25}.$$ | ||
| + | Zur Berechnung von $\varphi_c ( k = 2)$ muss über $3^3 = 27$ Kombinationen gemittelt werden. Das Ergebnis ist jedoch Null. | ||
| − | |||
| − | + | '''(6)''' Die Fouriertransformierte der zeitdiskreten AKF ${\rm A} \{ \varphi_c(\tau) \}$ lautet: | |
:$$P \{{\it \Phi_c}( f) \} = T\cdot \varphi_c ( k = 0) +2T \cdot \varphi_c ( k = 1) \cdot {\rm cos} ( 2 \pi f T ).$$ | :$$P \{{\it \Phi_c}( f) \} = T\cdot \varphi_c ( k = 0) +2T \cdot \varphi_c ( k = 1) \cdot {\rm cos} ( 2 \pi f T ).$$ | ||
| − | + | Mit dem Ergebnis der letzten Teilaufgabe folgt daraus: | |
:$$P \{{\it \Phi}_c( f) \} = \frac {T}{2} (1 - {\rm cos} ( 2 \pi f T ) )= T \cdot {\rm sin}^2 ( \pi f T ).$$ | :$$P \{{\it \Phi}_c( f) \} = \frac {T}{2} (1 - {\rm cos} ( 2 \pi f T ) )= T \cdot {\rm sin}^2 ( \pi f T ).$$ | ||
| − | + | Wie unter Punkt (2) gezeigt, gilt dann für das LDS – also die Fouriertransformierte von $\varphi_c(\tau)$: | |
:$${\it \Phi_c}( f) = T \cdot {\rm sin}^2 ( \pi f T ) \cdot {\rm si}^2 ( \pi f T ) = T \cdot \frac {{\rm sin}^4 ( \pi f T )}{( \pi f T )^2 } .$$ | :$${\it \Phi_c}( f) = T \cdot {\rm sin}^2 ( \pi f T ) \cdot {\rm si}^2 ( \pi f T ) = T \cdot \frac {{\rm sin}^4 ( \pi f T )}{( \pi f T )^2 } .$$ | ||
| − | + | :$$\Rightarrow \hspace{0.3cm} {\it \Phi_c}( f = 0) \hspace{0.15cm}\underline{= 0}, \hspace{0.8cm} | |
| − | : | + | {\it \Phi_c}( f = {\rm500 \hspace{0.1cm}kHz}) = T \cdot \frac {{\rm sin}^4 ( \pi /2 )}{( \pi /2 )^2 } = \frac {4 T}{\pi^2} \rm \hspace{0.15cm}\underline{= 0.405 \cdot 10^{-6} \ {1}/{Hz}}.$$ |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 29. März 2017, 13:18 Uhr
Zur Spektralanpassung (Formung) eines Digitalsignals an die Eigenschaften des Kanals verwendet man so genannte Pseudoternärcodes. Bei diesen Codes wird die binäre Quellensymbolfolge $\langle q_\nu \rangle$ nach einer festen Vorschrift in eine Folge $\langle c_\nu \rangle$ von Ternärsymbolen umgesetzt:
- $$q_{\nu} \in \{ -1,\hspace{0.1cm} +1 \} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_{\nu} \in \{ -1, \hspace{0.1cm}0, \hspace{0.1cm}+1 \} .$$
Der bekannteste Vertreter dieser Codeklasse ist der AMI-Code (von Alternate Mark Inversion). Hier wird
- der Binärwert $q_\nu = -1$ stets auf $c_\nu = 0$ abgebildet,
- während $q_\nu = +1$ abwechselnd (alternierend) durch die Ternärwerte $c_\nu = +1$ und $c_\nu = -1$ dargestellt wird.
Vereinbarungsgemäß wird beim ersten Auftreten von $q_\nu = +1$ das Ternärsymbol $c_\nu = +1$ ausgewählt.
Weiter wird vorausgesetzt, dass die zwei möglichen Quellensymbole jeweils gleichwahrscheinlich sind und die Quellensymbolfolge $\langle q_\nu \rangle$ keine inneren statistischen Bindungen aufweist. Somit sind alle diskreten AKF-Werte gleich $0$ mit Ausnahme von $\varphi_q(k=0)$: $$\varphi_q ( k \cdot T) = 0 \hspace{0.5cm} {\rm f alls} \hspace{0.5cm} k \not= 0.$$
Hierbei bezeichnet $T$ den Abstand der Quellen– bzw. Codesymbole. Verwenden Sie den Wert $T = 1 \hspace{0.05cm} \rm \mu s$.
Das Bild zeigt die gegebenen Autokorrelationsfunktionen. Bitte beachten Sie:
- Rot eingezeichnet sind jeweils die zeitdiskreten Darstellungen ${\rm A} \{ \varphi_q(\tau) \}$ und ${\rm A} \{ \varphi_c(\tau) \}$ der Autokorrelationsfunktionen, jeweils mit dem Bezugswert $T$ .
- Die blau dargestellten Funktionen zeigen die zeitkontinuierlichen Verläufe $\varphi_q(\tau)$ und $\varphi_c(\tau)$ der AKF, wobei Rechtecksignale vorausgesetzt sind.
Hinweise:
- Die Aufgabe gehört zum Kapitel Leistungsdichtespektrum.
- Bezug genommen wird auch auf das Kapitel Autokorrelationsfunktion sowie auf die Seite Numerische_LDS-Ermittlung.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Benutzen Sie die folgende Fourierkorrespondenz, wobei ${\rm \Delta} (t)$ einen um $t = 0$ symmetrischen Dreieckimpuls mit ${\rm \Delta} (t= 0) = 1$ und ${\rm \Delta} (t) = 0$ für $|t| \ge T$ bezeichnet:
- $${\rm \Delta} (t) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} T \cdot {\rm si}^2 ( \pi f T).$$
Fragebogen
Musterlösung
(2) Richtig sind die Lösungsvorschläge 1 und 3:
- Die zeitdiskrete AKF und deren Fouriertransformierte lauten:
- $${\rm A} \{ \varphi_q ( \tau ) \} = \varphi_q ( k = 0) \cdot T \cdot \delta (\tau) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{\it \Phi_q}( f) \} = \varphi_q ( k = 0) \cdot T = T.$$
- Es ist berücksichtigt, dass $\varphi_q(k=0)\sigma_q^2= 1$ ist. Das bedeutet: Die periodische Fortsetzung von ${\rm P} \{ {\it \Phi}_q(f) \}$ ergibt somit für alle Frequenzen den gleichen Wert.
- Dagegen kann die zeitkontinuierliche AKF wie folgt dargestellt werden: $ \varphi_q ( \tau ) = {\rm A} \{ \varphi_q ( \tau ) \} \star ( {\rm \Delta} ( \tau) / T ).$
- Das dazugehörige Leistungsdichtespektrum (Fouriertransformierte der AKF) ist dann das Produkt der Fouriertransformierten der beiden Faltungsterme: $ {\it \Phi_q} ( f) = {\rm P} \{ {\it \Phi_q}( f) \} \cdot {\rm si}^2 (\pi f T ) = T \cdot {\rm si}^2 (\pi f T ) .$
- Aufgrund der gewählten AKF-Interpolation (mit Geradenabschnitten) aus ihren Abtastwerten ergibt sich ein si2-förmiges LDS. Ein rechteckförmiges Spektrum (Lösungsvorschlag 2) würde sich nur bei si-förmiger Interpolation einstellen.
(3) Die codierte Folge lautet: $\langle +1, 0, -1, +1, 0, -1, +1, 0, 0, 0 \rangle$. Das 6. Symbol ist somit $c_6\hspace{0.15cm}\underline{= -1}$.
(4) Die Auftrittswahrscheinlichkeiten der Werte $-1$, $0$ und $+1$ sind $0.25, 0.5, 0.25$. Daraus folgt:
- $$\varphi_c ( k = 0) = 0.25 \cdot (-1)^2 + 0.5 \cdot 0^2 +0.25 \cdot (+1)^2\hspace{0.15cm}\underline{ = 0.5}. $$
(5) Für den AKF-Wert bei $k = 1$ betrachtet man das Produkt $c_{\nu} \cdot c_{\nu+1}$. Es ergeben sich die rechts gezeigten Kombinationen. Einen Beitrag liefern nur Produkte $c_{\nu} \cdot c_{\nu+1} \ne 0$ mit ${\rm}[c_{\nu} \cdot c_{\nu+1}] \ne 0$:
- $$\varphi_c ( k = 1) = {\rm Pr} \left [( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \right ] \cdot (+1) \cdot (-1) + {\rm Pr} \left [ ( c_{\nu} = -1) \cap ( c_{\nu + 1} = +1) \right ] \cdot (-1) \cdot (+1).$$
In der Tabelle sind diese Terme rot gekennzeichnet. Weiter gilt:
- $$ {\rm Pr} \left [ ( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \right ] = $$
- $$ = {\rm Pr} ( c_{\nu} = +1) \cdot {\rm Pr} \left ( c_{\nu + 1} = -1 | c_{\nu } = +1) \right ) = \frac{1}{4} \cdot \frac{1}{2}= \frac{1}{8} . $$
Hierbei ist vorausgesetzt, dass $+1$ mit der Wahrscheinlichkeit $0.25$ auftritt und danach $-1$ nur in der Hälfte der Fälle folgt. Das gleiche Ergebnis erhält man für den zweiten Beitrag. Damit gilt:
- $$\varphi_c ( k = 1) = \frac {1}{8} \cdot (+1)\cdot (-1) + \frac {1}{8} \cdot (-1)\cdot (+1) \hspace{0.15cm}\underline{= -0.25}.$$
- $$\varphi_c ( k = -1) = \varphi_c ( k = 1) \hspace{0.15cm}\underline{= -0.25}.$$
Zur Berechnung von $\varphi_c ( k = 2)$ muss über $3^3 = 27$ Kombinationen gemittelt werden. Das Ergebnis ist jedoch Null.
(6) Die Fouriertransformierte der zeitdiskreten AKF ${\rm A} \{ \varphi_c(\tau) \}$ lautet:
- $$P \{{\it \Phi_c}( f) \} = T\cdot \varphi_c ( k = 0) +2T \cdot \varphi_c ( k = 1) \cdot {\rm cos} ( 2 \pi f T ).$$
Mit dem Ergebnis der letzten Teilaufgabe folgt daraus:
- $$P \{{\it \Phi}_c( f) \} = \frac {T}{2} (1 - {\rm cos} ( 2 \pi f T ) )= T \cdot {\rm sin}^2 ( \pi f T ).$$
Wie unter Punkt (2) gezeigt, gilt dann für das LDS – also die Fouriertransformierte von $\varphi_c(\tau)$:
- $${\it \Phi_c}( f) = T \cdot {\rm sin}^2 ( \pi f T ) \cdot {\rm si}^2 ( \pi f T ) = T \cdot \frac {{\rm sin}^4 ( \pi f T )}{( \pi f T )^2 } .$$
- $$\Rightarrow \hspace{0.3cm} {\it \Phi_c}( f = 0) \hspace{0.15cm}\underline{= 0}, \hspace{0.8cm} {\it \Phi_c}( f = {\rm500 \hspace{0.1cm}kHz}) = T \cdot \frac {{\rm sin}^4 ( \pi /2 )}{( \pi /2 )^2 } = \frac {4 T}{\pi^2} \rm \hspace{0.15cm}\underline{= 0.405 \cdot 10^{-6} \ {1}/{Hz}}.$$