Stochastische Signaltheorie/Kreuzkorrelationsfunktion und Kreuzleistungsdichte: Unterschied zwischen den Versionen
| Zeile 9: | Zeile 9: | ||
{{Definition}}''':''' Für die '''Kreuzkorrelationsfunktion''' zweier stationärer und ergodischer Prozesse mit den Musterfunktionen $x(t)$ und $y(t)$ gilt: | {{Definition}}''':''' Für die '''Kreuzkorrelationsfunktion''' zweier stationärer und ergodischer Prozesse mit den Musterfunktionen $x(t)$ und $y(t)$ gilt: | ||
| − | $$\varphi_{xy}(\tau)={\rm E} [{x(t)\cdot y(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\rm d \it t.$$ | + | :$$\varphi_{xy}(\tau)={\rm E} [{x(t)\cdot y(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\rm d \it t.$$ |
{{end}} | {{end}} | ||
| Zeile 27: | Zeile 27: | ||
Wir betrachten dazu noch ein zweites Signal $y(t) = \alpha \cdot x (t - t_{\rm 0}),$ das sich von $x(t)$ nur durch einen Dämpfungsfaktor $α$ und eine Laufzeit $t_0$ unterscheidet, wobei dem obigen Bild $α =0.5$ und $t_0 = 3 \ \rm ms$ zugrunde liegen. Dieses gedämpfte und verschobene Signal besitzt die rot gezeichnete AKF | Wir betrachten dazu noch ein zweites Signal $y(t) = \alpha \cdot x (t - t_{\rm 0}),$ das sich von $x(t)$ nur durch einen Dämpfungsfaktor $α$ und eine Laufzeit $t_0$ unterscheidet, wobei dem obigen Bild $α =0.5$ und $t_0 = 3 \ \rm ms$ zugrunde liegen. Dieses gedämpfte und verschobene Signal besitzt die rot gezeichnete AKF | ||
| − | $$\varphi_{y}(\tau) = \alpha^2 \cdot \varphi_{x}(\tau) .$$ | + | :$$\varphi_{y}(\tau) = \alpha^2 \cdot \varphi_{x}(\tau) .$$ |
Die Verschiebung um $t_0$ ist in der AKF nicht zu erkennen im Gegensatz zur (grün dargestellten) KKF, für die folgende Beziehung gilt: | Die Verschiebung um $t_0$ ist in der AKF nicht zu erkennen im Gegensatz zur (grün dargestellten) KKF, für die folgende Beziehung gilt: | ||
| − | $$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$ | + | :$$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$ |
{{end}} | {{end}} | ||
==Eigenschaften der Kreuzkorrelationsfunktion== | ==Eigenschaften der Kreuzkorrelationsfunktion== | ||
Im Folgenden sind wesentliche Eigenschaften der Kreuzkorrelationsfunktion zusammengestellt und die wichtigsten Unterschiede zur AKF herausgearbeitet. | Im Folgenden sind wesentliche Eigenschaften der Kreuzkorrelationsfunktion zusammengestellt und die wichtigsten Unterschiede zur AKF herausgearbeitet. | ||
| − | *Die Bildung der Kreuzkorrelationsfunktion ist | + | *Die Bildung der Kreuzkorrelationsfunktion ist ''nicht kommutativ''. Vielmehr gibt es stets zwei unterschiedliche Funktionen, nämlich |
| − | $$\varphi_{xy}(\tau)={\rm E} [{x(t)\cdot y(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$ | + | :$$\varphi_{xy}(\tau)={\rm E} [{x(t)\cdot y(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$ |
| − | $$\varphi_{yx}(\tau)={\rm E} [{y(t)\cdot x(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$ | + | :$$\varphi_{yx}(\tau)={\rm E} [{y(t)\cdot x(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$ |
*Zwischen den beiden Funktionen besteht der Zusammenhang $φ_{yx}(τ) = φ_{xy}(–τ)$. Im Beispiel des letzten Abschnitts hätte $φ_{yx}(τ)$ sein Maximum bei $τ = –3 \ \rm ms$. | *Zwischen den beiden Funktionen besteht der Zusammenhang $φ_{yx}(τ) = φ_{xy}(–τ)$. Im Beispiel des letzten Abschnitts hätte $φ_{yx}(τ)$ sein Maximum bei $τ = –3 \ \rm ms$. | ||
| − | *Im Allgemeinen tritt das | + | *Im Allgemeinen tritt das ''KKF-Maximum'' nicht bei $τ = 0$ auf (Ausnahme: $y = α · x$) und dem KKF-Wert $φ_{xy}(τ = 0)$ kommt keine besondere, physikalisch interpretierbare Bedeutung zu wie bei der AKF, bei der dieser Wert die Prozessleistung wiedergibt. |
*Der Betrag der KKF ist nach der [https://de.wikipedia.org/wiki/Cauchy-Schwarzsche_Ungleichung Cauchy-Schwarzschen Ungleichung] für alle $τ$-Werte kleiner oder gleich dem geometrischen Mittel der beiden Signalleistungen: | *Der Betrag der KKF ist nach der [https://de.wikipedia.org/wiki/Cauchy-Schwarzsche_Ungleichung Cauchy-Schwarzschen Ungleichung] für alle $τ$-Werte kleiner oder gleich dem geometrischen Mittel der beiden Signalleistungen: | ||
| − | $$\varphi_{xy}( \tau) \le \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)}.$$ | + | :$$\varphi_{xy}( \tau) \le \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)}.$$ |
:Im Beispiel auf der letzten Seite gilt das Gleichheitszeichen: | :Im Beispiel auf der letzten Seite gilt das Gleichheitszeichen: | ||
| − | $$\varphi_{xy}( \tau = t_{\rm 0}) = \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)} = \alpha \cdot \varphi_{x}( \tau = {\rm 0}) .$$ | + | :$$\varphi_{xy}( \tau = t_{\rm 0}) = \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)} = \alpha \cdot \varphi_{x}( \tau = {\rm 0}) .$$ |
| − | *Beinhalten $x(t)$ und $y(t)$ keinen gemeinsamen periodischen Anteil, so zeigt der Grenzwert der KKF für $τ → ∞$ das Produkt der beiden Mittelwerte an: | + | *Beinhalten $x(t)$ und $y(t)$ keinen gemeinsamen periodischen Anteil, so zeigt der ''Grenzwert der KKF'' für $τ → ∞$ das Produkt der beiden Mittelwerte an: |
| − | $$\lim_{\tau \rightarrow \infty} \varphi _{xy} ( \tau ) = m_x \cdot m_y .$$ | + | :$$\lim_{\tau \rightarrow \infty} \varphi _{xy} ( \tau ) = m_x \cdot m_y .$$ |
| − | *Sind zwei Signale $x(t)$ und $y(t)$ unkorreliert, so gilt $φ_{xy}(τ) ≡$ 0, das heißt, es ist $φ_{xy}(τ) =$ 0 für alle Werte von $τ$. Diese Annahme ist beispielsweise bei der gemeinsamen Betrachtung eines Nutz- und eines Störsignals in den meisten Fällen gerechtfertigt. | + | *Sind zwei Signale $x(t)$ und $y(t)$ ''unkorreliert'', so gilt $φ_{xy}(τ) ≡$ 0, das heißt, es ist $φ_{xy}(τ) =$ 0 für alle Werte von $τ$. Diese Annahme ist beispielsweise bei der gemeinsamen Betrachtung eines Nutz- und eines Störsignals in den meisten Fällen gerechtfertigt. |
| − | *Es ist jedoch stets zu beachten, dass die KKF nur die linearen statistischen Bindungen zwischen den Signalen $x(t)$ und $y(t)$ beinhaltet. Bindungen anderer Art – wie beispielsweise für den Fall $y(t) = x(t)^2$ – werden dagegen bei der KKF-Bildung nicht berücksichtigt. | + | *Es ist jedoch stets zu beachten, dass die KKF nur die ''linearen statistischen Bindungen'' zwischen den Signalen $x(t)$ und $y(t)$ beinhaltet. Bindungen anderer Art – wie beispielsweise für den Fall $y(t) = x(t)^2$ – werden dagegen bei der KKF-Bildung nicht berücksichtigt. |
==Anwendungen der Kreuzkorrelationsfunktion== | ==Anwendungen der Kreuzkorrelationsfunktion== | ||
Version vom 29. März 2017, 13:41 Uhr
Inhaltsverzeichnis
Definition der Kreuzkorrelationsfunktion
Bei vielen technischen Anwendungen interessiert man sich für ein quantitatives Maß zur Beschreibung der statistischen Verwandtschaft zwischen verschiedenen Prozessen bzw. zwischen deren Mustersignalen. Ein solches Maß ist die Kreuzkorrelationsfunktion (KKF), die hier unter den Voraussetzungen von Stationarität und Ergodizität hergeleitet wird.
- $$\varphi_{xy}(\tau)={\rm E} [{x(t)\cdot y(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\rm d \it t.$$
Die erste Definitionsgleichung kennzeichnet die Erwartungswertbildung (Scharmittelung), während die zweite Gleichung die Zeitmittelung über eine (möglichst große) Messdauer $T_{\rm M}$ beschreibt.
Ein Vergleich mit der AKF-Definition zeigt viele Gemeinsamkeiten mit dieser. Setzt man $y(t) = x(t)$, so erhält man $φ_{xy}(τ) = φ_{xx}(τ)$, also die Autokorrelationsfunktion, für die in unserem Tutorial meist die vereinfachte Schreibweise $φ_x(τ)$verwendet wird.
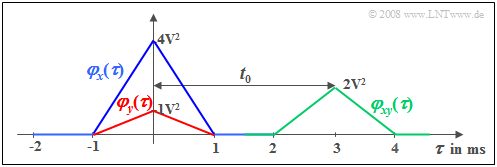
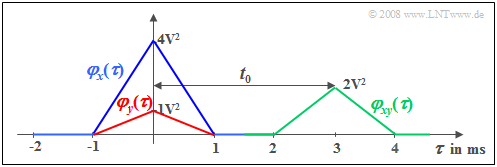
Wir betrachten ein Zufallssignal $x(t)$ mit dreieckförmiger AKF $φ_x(τ)$ ⇒ blaue Kurve. Diese AKF–Form ergibt sich zum Beispiel
- für ein Binärsignal mit gleichwahrscheinlichen bipolaren Amplitudenkoeffizienten ($+1$ bzw. $–1$) und
- bei rechteckförmigem Grundimpuls.
Wir betrachten dazu noch ein zweites Signal $y(t) = \alpha \cdot x (t - t_{\rm 0}),$ das sich von $x(t)$ nur durch einen Dämpfungsfaktor $α$ und eine Laufzeit $t_0$ unterscheidet, wobei dem obigen Bild $α =0.5$ und $t_0 = 3 \ \rm ms$ zugrunde liegen. Dieses gedämpfte und verschobene Signal besitzt die rot gezeichnete AKF
- $$\varphi_{y}(\tau) = \alpha^2 \cdot \varphi_{x}(\tau) .$$
Die Verschiebung um $t_0$ ist in der AKF nicht zu erkennen im Gegensatz zur (grün dargestellten) KKF, für die folgende Beziehung gilt:
- $$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$
Eigenschaften der Kreuzkorrelationsfunktion
Im Folgenden sind wesentliche Eigenschaften der Kreuzkorrelationsfunktion zusammengestellt und die wichtigsten Unterschiede zur AKF herausgearbeitet.
- Die Bildung der Kreuzkorrelationsfunktion ist nicht kommutativ. Vielmehr gibt es stets zwei unterschiedliche Funktionen, nämlich
- $$\varphi_{xy}(\tau)={\rm E} [{x(t)\cdot y(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$
- $$\varphi_{yx}(\tau)={\rm E} [{y(t)\cdot x(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$
- Zwischen den beiden Funktionen besteht der Zusammenhang $φ_{yx}(τ) = φ_{xy}(–τ)$. Im Beispiel des letzten Abschnitts hätte $φ_{yx}(τ)$ sein Maximum bei $τ = –3 \ \rm ms$.
- Im Allgemeinen tritt das KKF-Maximum nicht bei $τ = 0$ auf (Ausnahme: $y = α · x$) und dem KKF-Wert $φ_{xy}(τ = 0)$ kommt keine besondere, physikalisch interpretierbare Bedeutung zu wie bei der AKF, bei der dieser Wert die Prozessleistung wiedergibt.
- Der Betrag der KKF ist nach der Cauchy-Schwarzschen Ungleichung für alle $τ$-Werte kleiner oder gleich dem geometrischen Mittel der beiden Signalleistungen:
- $$\varphi_{xy}( \tau) \le \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)}.$$
- Im Beispiel auf der letzten Seite gilt das Gleichheitszeichen:
- $$\varphi_{xy}( \tau = t_{\rm 0}) = \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)} = \alpha \cdot \varphi_{x}( \tau = {\rm 0}) .$$
- Beinhalten $x(t)$ und $y(t)$ keinen gemeinsamen periodischen Anteil, so zeigt der Grenzwert der KKF für $τ → ∞$ das Produkt der beiden Mittelwerte an:
- $$\lim_{\tau \rightarrow \infty} \varphi _{xy} ( \tau ) = m_x \cdot m_y .$$
- Sind zwei Signale $x(t)$ und $y(t)$ unkorreliert, so gilt $φ_{xy}(τ) ≡$ 0, das heißt, es ist $φ_{xy}(τ) =$ 0 für alle Werte von $τ$. Diese Annahme ist beispielsweise bei der gemeinsamen Betrachtung eines Nutz- und eines Störsignals in den meisten Fällen gerechtfertigt.
- Es ist jedoch stets zu beachten, dass die KKF nur die linearen statistischen Bindungen zwischen den Signalen $x(t)$ und $y(t)$ beinhaltet. Bindungen anderer Art – wie beispielsweise für den Fall $y(t) = x(t)^2$ – werden dagegen bei der KKF-Bildung nicht berücksichtigt.
Anwendungen der Kreuzkorrelationsfunktion
Die Anwendungen der KKF in Nachrichtensystemen sind vielfältig. Hier einige Beispiele:
- Bei Amplitudenmodulation, aber auch bei BPSK-Systemen (Binary Phase Shift Keying) wird zur Demodulation (Rücksetzung des Signals in den ursprünglichen Frequenzbereich) sehr häufig der so genannte Synchrondemodulator verwendet, wobei auch beim Empfänger ein Trägersignal zugesetzt werden muss, und zwar frequenz– und phasensynchron zum Sender. Bildet man die KKF zwischen dem Empfangssignal und dem empfangsseitigen Trägersignal, so lässt sich anhand der Spitze der KKF die phasensynchrone Lage zwischen den beiden Signalen erkennen, und es kann bei Auseinanderdriften nachgeregelt werden.
- Das Mehrfachzugriffsverfahren CDMA (Code Division Multiple Access) wird zum Beispiel im Mobilfunkstandard UMTS angewendet. Es erfordert eine strenge Phasensynchronität, und zwar bezüglich der zugesetzten Pseudonoise-Folgen beim Sender (Bandspreizung) und beim Empfänger (Bandstauchung). Auch dieses Synchronisationsproblem löst man meist mittels der Kreuzkorrelationsfunktion.
- Mit Hilfe der Kreuzkorrelationsfunktion kann festgestellt werden, ob ein bekanntes Signal $s(t)$ in einem verrauschten Empfangssignal $r(t) = α · s(t – t_0) + n(t)$ vorhanden ist oder nicht, und wenn ja, zu welchem Zeitpunkt $t_0$ es auftritt. Aus dem berechneten Wert für $t_0$ lässt sich dann beispielsweise eine Fahrgeschwindigkeit ermitteln (Radartechnik). Diese Aufgabenstellung kann auch mit dem so genannten Matched-Filter gelöst werden, das in Kapitel 5.4 noch eingehend beschrieben wird und das viele Gemeinsamkeiten mit der Kreuzkorrelationsfunktion aufweist.
- Beim so genannten Korrelationsempfänger verwendet man die KKF zur Signaldetektion. Hierbei bildet man die Kreuzkorrelation zwischen dem durch Rauschen und eventuell auch durch Verzerrungen verfälschten Empfangssignal $r(t)$ und allen möglichen Sendesignalen $s_i(t)$, wobei für den Laufindex $i =$ 1, ..., $I$ gelten soll. Entscheidet man $N$ Binärsymbole gemeinsam, so ist $I = {\rm 2}^N$. Man entscheidet sich dann für die Symbolfolge mit dem größten KKF-Wert und erreicht so die minimale Fehlerwahrscheinlichkeit entsprechend der Maximum-Likelihood-Entscheidungsregel.
Kreuzleistungsdichtespektrum
Für manche Anwendungen kann es durchaus vorteilhaft sein, die Korrelation zwischen zwei Zufallssignalen im Frequenzbereich zu beschreiben.
Die beiden Kreuzleistungsdichtespektren ${\it Φ}_{xy}(f)$ und ${\it Φ}_{yx}(f)$ ergeben sich aus den dazugehörigen Kreuzkorrelationsfunktionen durch die Fouriertransformation: $${\it \Phi}_{xy}(f)=\int^{+\infty}_{-\infty}\varphi_{xy}({\it \tau}) \cdot {\rm e}^{{\rm -j}\pi f \tau} \rm d \it \tau, $$ $${\it \Phi}_{yx}(f)=\int^{+\infty}_{-\infty}\varphi_{yx}({\it \tau}) \cdot {\rm e}^{{\rm -j}\pi f \tau} \rm d \it \tau.$$ Manchmal wird hierfür auch der Begriff spektrale Kreuzleistungsdichte verwendet.
Es gilt hier der gleiche Zusammenhang wie zwischen einem deterministischen Signal $x(t)$ und seinem Spektrum $X(f)$ bzw. zwischen der Autokorrelationsfunktion ${\it φ}_x(τ)$ eines ergodischen Prozesses { $x_i(t)$} und dem dazugehörigen Leistungsdichtespektrum ${\it Φ}_x(f)$. Ebenso beschreibt bei diesen Beispielen die Fourierrücktransformation ⇒ „Zweites Fourierintegral” den Übergang vom Spektralbereich in den Zeitbereich.
Wir nehmen hier Bezug zum Beispiel auf der Seite Definition der KKF mit den beiden „rechteckförmigen Zufallsgrößen” $x(t)$ und $y(t) = α · x(t – t_0)$. Da die AKF ${\it φ}_x(τ)$ dreieckförmig verläuft, ist – wie in Kapitel 4.5 beschrieben – das LDS ${\it Φ}_x(f) \hspace{0.1cm}{\rm si}^2$-förmig.
Welche Aussagen können wir aus dieser Grafik für die Spektralfunktionen ableiten?
- Im zitierten Beispiel haben wir festgestellt, dass sich die Autokorrelationsfunktion ${\it φ}_y(τ)$ von ${\it φ}_x(τ)$ nur um den konstanten Faktor $α^2$ unterscheidet.
- Damit ist klar, dass das Leistungsdichtespektrum ${\it Φ}_y(f)$ von ${\it \Phi}_x(f)$ ebenfalls nur um diesen konstanten Faktor $α^2$ abweicht. Beide Spektralfunktionen sind reell.
- Dagegen besitzt das Kreuzleistungsdichtespektrum einen komplexen Funktionsverlauf:
$${\it \Phi}_{xy}(f) ={\it \Phi}^\star_{yx}(f)= \alpha \cdot {\it \Phi}_{x}(f) \hspace{0.05cm}\cdot {\rm e}^{- {\rm j } \hspace{0.02cm}\pi f t_0}.$$