Aufgaben:Aufgabe 4.16Z: Zwei- und dreidimensionale Datenreduktion: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 19: | Zeile 19: | ||
:Den Quotienten <i>N</i><sub>2</sub>'/<i>N</i><sub>2</sub> bezeichnen wir als Datenreduktionsfaktor bezüglich der 2D-Zufallsgröße <b>y</b>. In analoger Definition ist <i>N</i><sub>3</sub>'/<i>N</i><sub>3</sub> der entsprechende Reduktionsfaktor der 3D-Zufallsgröße <b>z</b> für <i>Δ<sub>x</sub></i> = <i>Δ<sub>y</sub></i> = <i>Δ<sub>z</sub></i> = 1/32. Anzumerken ist, dass in beiden Fällen ein möglichst kleiner Wert günstig ist. | :Den Quotienten <i>N</i><sub>2</sub>'/<i>N</i><sub>2</sub> bezeichnen wir als Datenreduktionsfaktor bezüglich der 2D-Zufallsgröße <b>y</b>. In analoger Definition ist <i>N</i><sub>3</sub>'/<i>N</i><sub>3</sub> der entsprechende Reduktionsfaktor der 3D-Zufallsgröße <b>z</b> für <i>Δ<sub>x</sub></i> = <i>Δ<sub>y</sub></i> = <i>Δ<sub>z</sub></i> = 1/32. Anzumerken ist, dass in beiden Fällen ein möglichst kleiner Wert günstig ist. | ||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Verallgemeinerung_auf_N-dimensionale_Zufallsgrößen|Verallgemeinerung auf N-dimensionale Zufallsgrößen]]. | ||
| + | *Einige Grundlagen zur Anwendung von Vektoren und Matrizen finden sich auf den Seiten [[Stochastische_Signaltheorie/Verallgemeinerung_auf_N-dimensionale_Zufallsgrößen#Grundlagen_der_Matrizenrechnung:_Determinante_einer_Matrix|Determinante einer Matrix]] sowie [[Stochastische_Signaltheorie/Verallgemeinerung_auf_N-dimensionale_Zufallsgrößen#Grundlagen_der_Matrizenrechnung:_Inverse_einer_Matrix|Inverse einer Matrix]] | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Insbesondere ist zu beachten: Eine $2×2$-Kovarianzmatrix besitzt zwei reelle Eigenwerte $\lambda_1$ und $\lambda_2$. Diese beiden Eigenwerte bestimmen zwei Eigenvektoren $\xi_1$ und $\xi_2$. Diese spannen ein neues Koordinatensystem in Richtung der Hauptachsen des alten Systems auf. | ||
| + | * Entsprechend der Seite [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen#H.C3.B6henlinien_bei_korrelierten_Zufallsgr.C3.B6.C3.9Fen|Höhenlinien bei korrelierten Zufallsgrößen]] ist der Winkel $\alpha$ zwischen dem alten und dem neuen System durch folgende Gleichung gegeben: | ||
| + | :$$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot | ||
| + | \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2}).$$ | ||
:<b>Hinweis:</b> Diese Aufgabe bezieht sich auf die Seite Eigenwerte und Eigenvektoren im Kapitel 4.7. Die Bestimmungsgleichung der Eigenwerte von <b>K<sub>z</sub></b> lautet: | :<b>Hinweis:</b> Diese Aufgabe bezieht sich auf die Seite Eigenwerte und Eigenvektoren im Kapitel 4.7. Die Bestimmungsgleichung der Eigenwerte von <b>K<sub>z</sub></b> lautet: | ||
Version vom 3. April 2017, 14:16 Uhr
- Wir betrachten Gaußsche mittelwertfreie Zufallsgrößen x, y und z mit den Dimensionen N = 1, N = 2 und N = 3:
- Die eindimensionale Zufallsgröße x ist durch die Varianz σ2 = 1 bzw. die Streuung σ = 1 charakterisiert. Wegen der Dimension N = 1 gilt x = x.
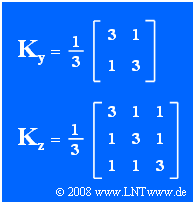
- Der Korrelationskoeffizient zwischen den Komponenten y1 und y2 der 2D-Zufallsgröße y beträgt ρ = 1/3 (siehe Matrix Ky). y1 und y2 weisen ebenfalls die Streuung σ = 1 auf.
- Die Statistik der dreidimensionalen Zufallsgröße z ist durch die Korrelationsmatrix Kz vollständig bestimmt.
- Quantisiert man die Zufallsgröße x im Bereich zwischen –4 und +4 mit Intervallbreite Δx = 1/32, so gibt es insgesamt N1 = 256 unterschiedliche Quantisierungswerte, für deren Übertragung somit n1 = 8 Bit benötigt würden.
- Analog ergeben sich bei der Zufallsgröße y insgesamt N2 = 2562 = 65536 unterschiedliche quantisierte Wertepaare, wenn man die Korrelation zwischen y1 und y2 nicht berücksichtigt. Durch Ausnutzung dieser Korrelation – zum Beispiel durch Koordinatentransformation vom Ursprungsystem (y1, y2) zum neuen System (η1, η2) – ergibt sich eine geringere Zahl N2' quantisierter Wertepaare.
- Hierbei ist zu berücksichtigen, dass jede Komponente entsprechend ihrer jeweiligen Streuung (σ1 bzw. σ2) im Bereich von –4σi bis +4σi zu quantisieren ist und die Quantisierungsintervalle in beiden Richtungen gleich sein sollen: Δx = Δy = 1/32.
- Den Quotienten N2'/N2 bezeichnen wir als Datenreduktionsfaktor bezüglich der 2D-Zufallsgröße y. In analoger Definition ist N3'/N3 der entsprechende Reduktionsfaktor der 3D-Zufallsgröße z für Δx = Δy = Δz = 1/32. Anzumerken ist, dass in beiden Fällen ein möglichst kleiner Wert günstig ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel Verallgemeinerung auf N-dimensionale Zufallsgrößen.
- Einige Grundlagen zur Anwendung von Vektoren und Matrizen finden sich auf den Seiten Determinante einer Matrix sowie Inverse einer Matrix
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Insbesondere ist zu beachten: Eine $2×2$-Kovarianzmatrix besitzt zwei reelle Eigenwerte $\lambda_1$ und $\lambda_2$. Diese beiden Eigenwerte bestimmen zwei Eigenvektoren $\xi_1$ und $\xi_2$. Diese spannen ein neues Koordinatensystem in Richtung der Hauptachsen des alten Systems auf.
- Entsprechend der Seite Höhenlinien bei korrelierten Zufallsgrößen ist der Winkel $\alpha$ zwischen dem alten und dem neuen System durch folgende Gleichung gegeben:
- $$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2}).$$
- Hinweis: Diese Aufgabe bezieht sich auf die Seite Eigenwerte und Eigenvektoren im Kapitel 4.7. Die Bestimmungsgleichung der Eigenwerte von Kz lautet:
- $$\lambda^3 - 3 \lambda^2 + \frac{24}{9}\lambda - \frac{20}{27} = 0.$$
- Eine der drei Lösungen dieser Gleichung ist λ1 = 5/3.
Fragebogen
Musterlösung
- 1. Aus der Bedingung Ky – λ · E = 0 folgt:
- $${\rm det}\left[ \begin{array}{cc} 1- \lambda & 1/3 \\ 1/3 & 1- \lambda \end{array} \right] = (1-\lambda)^2 -\frac{1}{9} = 0$$
- $$\Rightarrow \hspace{0.3cm}\lambda^2 -2\lambda+ \frac{8}{9}= 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\lambda_{1/2}= 1 \pm \sqrt{1-\frac{8}{9}}= 1 \pm \frac{1}{3}.$$
- Die Eigenwerte dieser 2×2-Matrix sind somit λ1 = 4/3 und λ2 = 2/3.
- 2. Ohne Berücksichtigung von Korrelationen gibt es
- $$N_2 = \left( \frac{8}{\it \Delta_x}\right)^2= 256^2 = 65536$$
- verschiedene Wertepaare. Unter Berücksichtigung der Korrelationen und des Sachverhaltes, dass die beiden durch Koordinatendrehung entstandenen Komponenten η1 und η2 jeweils im Bereich von –4σ1 bis +4σ1 (bzw. von –4σ2 bis +4σ2) zu quantisieren sind, erhält man
- $$N_2' = \frac{8 \hspace{0.05cm}\sigma_1}{\it \Delta_x}\cdot\frac{8 \hspace{0.05cm}\sigma_2}{\it \Delta_y}= N_2 \cdot \sigma_1 \cdot \sigma_2 .$$
- Der Quotient lautet somit mit σ12 = λ1 und σ22 = λ2:
- $$\frac{N_2'}{N_2} = \sigma_1 \cdot \sigma_2 = \sqrt{{4}/{3}} \cdot \sqrt{{2}/{3}} = \frac{2 \cdot \sqrt{2}}{3} \hspace{0.15cm}\underline{ \approx 0.943}.$$
- 3. Die Bestimmungsgleichung der Eigenwerte von Kz lautet:
- $${\rm det} \left[ \begin{array}{ccc} 1-\lambda & 1/3 & 1/3\\ 1/3 & 1-\lambda & 1/3\\ 1/3 & 1/3 & 1-\lambda \end{array}\right] = 0$$
- $$\Rightarrow \hspace{0.3cm}(1- \lambda) \left[(1- \lambda)^2 - \frac{1}{9} \right]- \frac{1}{3} \left[\frac{1}{3}(1- \lambda) - \frac{1}{9} \right] + \frac{1}{3} \left[\frac{1}{9} - \frac{1}{3}(1- \lambda) \right] = 0$$
- $$\Rightarrow \hspace{0.3cm}(1- \lambda) (\lambda^2 -2\lambda+ \frac{8}{9})- \frac{1}{9} (\frac{2}{3}- \lambda )+ \frac{1}{9} ( \lambda - \frac{2}{3})= 0$$
- $$\Rightarrow \hspace{0.3cm}\lambda^2 - 2\lambda + \frac{8}{9} - \lambda^3 + 2 \lambda^2 - \frac{8}{9}\lambda - \frac{4}{27} + \frac{2}{9}\lambda = 0$$
- $$\Rightarrow \hspace{0.3cm}\lambda^3 - 3 \lambda^2 + \frac{24}{9}\lambda - \frac{20}{27} = 0.$$
- Diese Gleichung wurde bereits als Lösungshinweis angegeben, ebenso wie eine der Lösungen: <nobr>λ1 = 5/3.</nobr> Damit ergibt sich die Bestimmungsgleichung für die weiteren Eigenwerte λ2 und λ3 zu
- $$\frac{\lambda^3 - 3 \lambda^2 + {24}/{9}\lambda - {20}/{27}}{\lambda -{5}/{3}} = \lambda^2 - {4}/{3} \cdot \lambda + {4}/{9} =0.$$
- Diese Bestimmungsgleichung lässt sich wie folgt umformen:
- $$(\lambda - {2}/{3})^2 =0.$$
- Die weiteren Eigenwerte neben λ1 = 5/3 sind somit gleich und ergeben sich zu λ2 = λ3 = 2/3.
- 4. Analog zur Vorgehensweise unter Punkt b) ergibt sich hier:
- $$\frac{N_3'}{N_3} = \sqrt{\lambda_1 \cdot \lambda_2\cdot \lambda_3} = \sqrt{\frac{5}{3} \cdot \frac{2}{3}\cdot \frac{2}{3}} = \sqrt{\frac{20}{27}} \hspace{0.15cm}\underline{ \approx 0.861}.$$