Aufgaben:Aufgabe 4.2Z: Gemischte Zufallsgrößen: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 4.02Z Gemischte Zufallsgrößen nach 4.2Z Gemischte Zufallsgrößen) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2868__Inf_Z_4_2_neu.png|right|]] | + | [[Datei:P_ID2868__Inf_Z_4_2_neu.png|right|WDF von <i>X</i> und VTF von <i>Y</i>]] |
Man spricht von einer <i>gemischten Zufallsgröße</i>, wenn die Zufallsgröße neben einem kontinuierlichen Anteil auch noch diskrete Anteile beinhaltet. | Man spricht von einer <i>gemischten Zufallsgröße</i>, wenn die Zufallsgröße neben einem kontinuierlichen Anteil auch noch diskrete Anteile beinhaltet. | ||
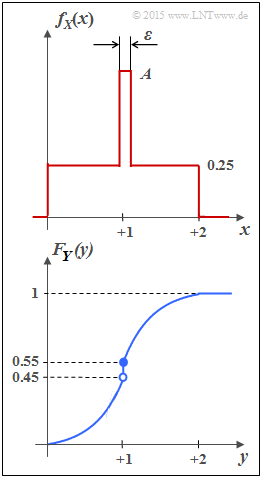
| − | Die Zufallsgröße | + | *Die Zufallsgröße $Y$ mit der [[Stochastische_Signaltheorie/Verteilungsfunktion|Verteilungsfunktion]] $F_Y(y)$ gemäß der unteren Skizze besitzt beispielsweise sowohl einen kontinuierlichen als auch einen diskreten Anteil. |
| + | *Die [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion|Wahrscheinlichkeitsdichtefunktion] $f_Y(y)$ erhält man aus $F_Y(y)$ durch Differentiation. | ||
| + | *Aus dem Sprung bei $y= 1$ in der Verteilungsfunktion (VTF) wird somit ein „Dirac” in der Wahrscheinlichkeitsdichtefunktion (WDF). | ||
| − | In der Teilaufgabe ( | + | In der Teilaufgabe $(4)$ soll die differentielle Entropie $h(Y)$ der Zufallsgröße $Y$ ermittelt werden (in bit), wobei von folgender Gleichung auszugehen ist: |
| − | $$h(Y) = | + | :$$h(Y) = |
\hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_Y(y) ] \hspace{0.1cm}{\rm d}y | \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_Y(y) ] \hspace{0.1cm}{\rm d}y | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
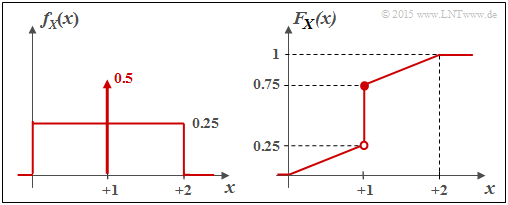
| − | + | *In der Teilaufgabe $(2)$ ist die differentielle Entropie $h(X)$ der Zufallsgröße $X$ zu berechnen, deren WDF $f_X(x)$ oben skizziert ist. Führt man einen geeigneten Grenzübergang durch, so wird auch aus der Zufallsgröße $X$ eine gemischte Zufallsgröße. | |
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Differentielle_Entropie|Differentielle Entropie]]. | ||
| + | *Weitere Informationen zu gemischten Zufallsgrößen finden Sie im Kapitel [[Stochastische_Signaltheorie/Verteilungsfunktion|Verteilungsfunktion]] des Buches „Stochastische Signaltheorie”. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
Version vom 6. April 2017, 12:58 Uhr
Man spricht von einer gemischten Zufallsgröße, wenn die Zufallsgröße neben einem kontinuierlichen Anteil auch noch diskrete Anteile beinhaltet.
- Die Zufallsgröße $Y$ mit der Verteilungsfunktion $F_Y(y)$ gemäß der unteren Skizze besitzt beispielsweise sowohl einen kontinuierlichen als auch einen diskreten Anteil.
- Die [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion|Wahrscheinlichkeitsdichtefunktion] $f_Y(y)$ erhält man aus $F_Y(y)$ durch Differentiation.
- Aus dem Sprung bei $y= 1$ in der Verteilungsfunktion (VTF) wird somit ein „Dirac” in der Wahrscheinlichkeitsdichtefunktion (WDF).
In der Teilaufgabe $(4)$ soll die differentielle Entropie $h(Y)$ der Zufallsgröße $Y$ ermittelt werden (in bit), wobei von folgender Gleichung auszugehen ist:
- $$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_Y(y) ] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$
- In der Teilaufgabe $(2)$ ist die differentielle Entropie $h(X)$ der Zufallsgröße $X$ zu berechnen, deren WDF $f_X(x)$ oben skizziert ist. Führt man einen geeigneten Grenzübergang durch, so wird auch aus der Zufallsgröße $X$ eine gemischte Zufallsgröße.
Hinweise:
- Die Aufgabe gehört zum Kapitel Differentielle Entropie.
- Weitere Informationen zu gemischten Zufallsgrößen finden Sie im Kapitel Verteilungsfunktion des Buches „Stochastische Signaltheorie”.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
b) Die differentielle Entropie (in „bit”) ist wie folgt gegeben: $$h(X) = \hspace{0.1cm} \hspace{-0.45cm} \int\limits_{{\rm supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{f_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ Wir unterteilen nun das Integral in drei Teilintegrale: $$h(X) \hspace{-0.15cm} = \hspace{-0.15cm} \hspace{-0.25cm} \int\limits_{0}^{1-\varepsilon/2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x + \hspace{-0.25cm}\int\limits_{1+\varepsilon/2}^{2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x $$ $$\ + \hspace{-0.15cm}\hspace{-0.25cm}\int\limits_{1-\varepsilon/2}^{1+\varepsilon/2} \hspace{-0.15cm} [0.5/\varepsilon + 0.25] \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5/\varepsilon + 0.25} \hspace{0.1cm}{\rm d}x $$ $$=\ \hspace{-0.15cm} 2 \cdot 0.25 \cdot 2 \cdot (2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25) \hspace{0.05cm}.$$ Insbesondere erhält man
- für ε = 0.1:
$$h(X) =1.9 - 0.525 \cdot {\rm log}_2 \hspace{0.1cm}(5.25) = 1.9 - 1.256 \hspace{0.15cm}\underline{= 0.644\,{\rm bit}} \hspace{0.05cm},$$
- für ε = 0.01:
$$h(X) =1.99 - 0.5025 \cdot {\rm log}_2 \hspace{0.1cm}(50.25)= 1.99 - 2.84 \hspace{0.15cm}\underline{= -0.850\,{\rm bit}} \hspace{0.05cm}$$
- für ε = 0.001:
$$h(X) =1.999 - 0.50025 \cdot {\rm log}_2 \hspace{0.1cm}(500.25) = 1.999 - 8.967 \hspace{0.15cm}\underline{= -6.968\,{\rm bit}} \hspace{0.05cm}.$$ c) Alle Lösungsvorschläge sind hier zutreffend. Nach dem Grenzübergang ε → 0 erhält man für die differentielle Entropie $$h(X) \hspace{-0.15cm} = \hspace{-0.15cm} \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0} \hspace{0.1cm}[(2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25)]$$ $$ = \ \hspace{-0.15cm} 2\,{\rm bit} - 0.5 \cdot \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}{\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} - \infty \hspace{0.05cm}.$$ Die Wahrscheinlichkeitsdichtefunktion (WDF) ergibt sich in diesem Fall zu $$f_X(x) = \left\{ \begin{array}{c} 0.25 + 0.5 \cdot \delta (x-1) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 2, \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.$$ Es handelt sich demzufolge um eine „gemischte” Zufallsgröße mit
- einem stochastischen, gleichverteilten Anteil zwischen 0 ≤ x ≤ 2, und
- einem diskreten Anteil bei x = 1 mit der Wahrscheinlichkeit 0.5.
Die Grafik zeigt links die WDF fX(x) und rechts die Verteilungsfunktion (kurz VTF) FX(x).
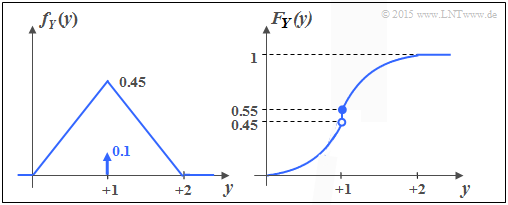
d) Richtig sind die Lösungsvorschläge 2, 3 und 5. Die untere Grafik zeigt die WDF und die VTF der Zufallsgröße Y. Man erkennt:
- Y beinhaltet wie X sowohl einen kontinuierlichen als auch einen diskreten Anteil.
- Der diskrete Anteil tritt mit der Wahrscheinlichkeit Pr(Y = 1) = 0.1 auf.
- Da FY(y) = Pr(Y ≤ y) gilt, ergibt sich der rechtsseitige Grenzwert: FY(y = 1) = 0.55.
- Der kontinuierliche Anteil ist nicht gleichverteilt; vielmehr liegt eine Dreieckverteilung vor.
Richtig ist auch der letzte Vorschlag: h(Y) = h(X) = –∞. Denn: Bei einer jeden Zufallsgröße mit einem diskreten Anteil – und ist er auch noch so klein, ist die differentielle Entropie gleich minus unendlich.