Aufgaben:Aufgabe 4.8: Numerische Auswertung der AWGN-Kanalkapazität: Unterschied zwischen den Versionen
Khalil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/AWGN–Kanalkapazität bei wertdiskretem Eingang }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {…“) |
Khalil (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID2936__Inf_A_4_8_Tab.png|right|]] |
| + | Für die Kanalkapazität <i>C</i> des AWGN–Kanals als obere Schranke für die Coderate <i>R</i> bei Digitalsignalübertragung gibt es zwei verschiedene Gleichungen : | ||
| + | |||
| + | '''Kanalkapazität <i>C</i> in Abhängigkeit von <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>: ''' | ||
| + | $$C( E_{\rm S}/{N_0}) = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot E_{\rm S}}{N_0}) .$$ | ||
| + | Hierbei sind folgende Abkürzungen verwendet: | ||
| + | :* <i>E</i><sub>S</sub>: die Energie pro Symbol des Digitalsignals, | ||
| + | :* <i>N</i><sub>0</sub>: die AWGN–Rauschleistungsdichte. | ||
| + | |||
| + | '''Kanalkapazität <i>C</i> in Abhängigkeit von <i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>:''' | ||
| + | $$C( E_{\rm B}/{N_0}) = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) .$$ | ||
| + | |||
| + | Berücksichtigt ist der Zusammenhang <i>E</i><sub>S</sub> = <i>R</i> · <i>E</i><sub>B</sub>, wobei <i>R</i> die Coderate der bestmöglichen Kanalcodierung angibt. Eine fehlerfreie Übertragung (unter Berücksichtigung dieses optimalen Codes) ist für das gegebene <i>E</i><sub>B</sub>/<i>N</i><sub>0</sub> möglich, so lange <i>R</i> ≤ <i>C</i> gilt ⇒ [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Definition_und_Bedeutung_der_Kanalkapazit.C3.A4t|''Kanalcodierungstheorem von Shannon.''']] | ||
| + | |||
| + | Durch die Tabelle vorgegeben ist der Kurvenverlauf <i>C</i>(<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>). Im Mittelpunkt dieser Aufgabe steht die numerische Auswertung der zweiten Gleichung. | ||
| + | '''Hinweis''' | ||
| + | :* Die Aufgabe gehört zum Themengebiet von [[Informationstheorie/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang|'''Kapitel 4.3.''']] | ||
Version vom 18. April 2017, 18:51 Uhr
Für die Kanalkapazität C des AWGN–Kanals als obere Schranke für die Coderate R bei Digitalsignalübertragung gibt es zwei verschiedene Gleichungen :
Kanalkapazität C in Abhängigkeit von ES/N0: $$C( E_{\rm S}/{N_0}) = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot E_{\rm S}}{N_0}) .$$ Hierbei sind folgende Abkürzungen verwendet:
- ES: die Energie pro Symbol des Digitalsignals,
- N0: die AWGN–Rauschleistungsdichte.
Kanalkapazität C in Abhängigkeit von EB/N0: $$C( E_{\rm B}/{N_0}) = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) .$$
Berücksichtigt ist der Zusammenhang ES = R · EB, wobei R die Coderate der bestmöglichen Kanalcodierung angibt. Eine fehlerfreie Übertragung (unter Berücksichtigung dieses optimalen Codes) ist für das gegebene EB/N0 möglich, so lange R ≤ C gilt ⇒ Kanalcodierungstheorem von Shannon.'
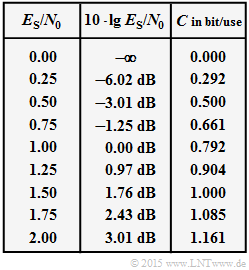
Durch die Tabelle vorgegeben ist der Kurvenverlauf C(ES/N0). Im Mittelpunkt dieser Aufgabe steht die numerische Auswertung der zweiten Gleichung. Hinweis
- Die Aufgabe gehört zum Themengebiet von Kapitel 4.3.
Fragebogen
Musterlösung