Aufgaben:Aufgabe 1.7: Entropie natürlicher Texte: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
}} | }} | ||
| − | [[Datei:P_ID2319__Inf_A_1_7_neu.png|right|]] | + | [[Datei:P_ID2319__Inf_A_1_7_neu.png|right|Text mit Auslöschungen bzw. Fehlern]] |
| − | + | Anfang der 1950er Jahre schätzte [https://de.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon] die Entropie $H$ der englischen Sprache mit einem bit pro Zeichen ab. Kurze Zeit später kam [https://de.wikipedia.org/wiki/Karl_K%C3%BCpfm%C3%BCller Karl Küpfmüller] bei einer empirischen Untersuchung der deutschen Sprache auf einen Entropiewert von $H =1.3\ \rm bit/Zeichen$, also einen etwas größeren Wert. Die Ergebnisse von Shannon und Küpfmüller beruhen dabei interessanter Weise auf zwei völlig unterschiedlichen Methoden. | |
| − | + | Die differierenden Ergebnisse lassen sich eher nicht mit den geringen Differenzen hinsichtlich des Symbolumfangs $M$ erklären: | |
| − | + | * Shannon ging von 26 Buchstaben und dem Leerzeichen aus ⇒ $M = 27$. | |
| + | * Küpfmüller ging dagegen von $M = 267$ Buchstaben aus, ebenfalls ohne zwischen Groß– und Kleinschreibung zu unterscheiden. | ||
| − | |||
| − | + | Mit dieser Aufgabe soll gezeigt werden, wie sich | |
| + | * Auslöschungen (<i>Erasures</i>) ⇒ man kennt den Ort eines Fehlers, | ||
| + | * Zeichenfehler (<i>Errors</i>) ⇒ es ist nicht offensichtlich, was falsch und was richtig ist, | ||
| − | + | auf die Verständlichkeit eines Textes auswirken. Unser Text beinhaltet dabei auch die typisch deutschen Buchstaben „ä”, „ö”, „ü” und „ß” sowie Ziffern und Interpunktion. Außerdem wird zwischen Groß– und Kleinschreibung unterschieden. | |
| − | |||
| − | + | In der Abbildung ist dieser Text, der von Küpfmüllers Vorgehensweise handelt, in sechs Blöcke der Länge zwischen $N = 197$ bis $N = 319$ aufgeteilt. Beschrieben ist die Überprüfung seiner [[Informationstheorie/Natürliche_wertdiskrete_Nachrichtenquellen#Eine_weitere_Entropieabsch.C3.A4tzung_von_K.C3.BCpfm.C3.BCller|ersten Analyse]] auf völlig anderem Wege, die zum Ergebnis $H =1.51\ \rm bit/Zeichen$ führte. | |
| − | + | * In den oberen fünf Blöcken erkennt man <i>Erasures</i> mit verschiedenen Auslöschwahrscheinlichkeiten zwischen 10% und 50%. | |
| − | + | * Im letzten Block sind <i>Zeichenfehler</i> mit 20–prozentiger Verfälschungswahrscheinlichkeit eingefügt. | |
| − | + | Der Einfluss solcher Zeichenfehler auf die Lesbarkeit eines Textes soll in der Teilaufgabe (4) verglichen werden mit dem zweiten (rot umrandeten) Block, für den die Wahrscheinlichkeit eines Erasures ebenfalls 20% beträgt. | |
| − | |||
| − | |||
| − | |||
| − | |||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Informationstheorie/Nachrichtenquellen_mit_Gedächtnis|Nachrichtenquellen mit Gedächtnis]]. | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Nachrichtenquellen_mit_Gedächtnis|Nachrichtenquellen mit Gedächtnis]]. | ||
| − | *Bezug genommen wird insbesondere auf die | + | *Bezug genommen wird insbesondere auf die beiden Seiten |
| − | + | [[Informationstheorie/Natürliche_wertdiskrete_Nachrichtenquellen#Entropieabsch.C3.A4tzung_nach_K.C3.BCpfm.C3.BCller|Entropieabschätzung nach Küpfmüller]] sowie [[Informationstheorie/Natürliche_wertdiskrete_Nachrichtenquellen#Eine_weitere_Entropieabsch.C3.A4tzung_von_K.C3.BCpfm.C3.BCller|eine weitere Entropieabschätzung nachvon Küpfmüller]]. | |
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| − | + | *Für die ''relative Redundanz'' einer Folge gilt mit dem Entscheidungsgehalt $H_0$ und der Entropie $H$ gilt: | |
| − | |||
:$$r = \frac{H_0 - H}{H_0}\hspace{0.05cm}.$$ | :$$r = \frac{H_0 - H}{H_0}\hspace{0.05cm}.$$ | ||
Version vom 3. Mai 2017, 09:57 Uhr
Anfang der 1950er Jahre schätzte Claude E. Shannon die Entropie $H$ der englischen Sprache mit einem bit pro Zeichen ab. Kurze Zeit später kam Karl Küpfmüller bei einer empirischen Untersuchung der deutschen Sprache auf einen Entropiewert von $H =1.3\ \rm bit/Zeichen$, also einen etwas größeren Wert. Die Ergebnisse von Shannon und Küpfmüller beruhen dabei interessanter Weise auf zwei völlig unterschiedlichen Methoden.
Die differierenden Ergebnisse lassen sich eher nicht mit den geringen Differenzen hinsichtlich des Symbolumfangs $M$ erklären:
- Shannon ging von 26 Buchstaben und dem Leerzeichen aus ⇒ $M = 27$.
- Küpfmüller ging dagegen von $M = 267$ Buchstaben aus, ebenfalls ohne zwischen Groß– und Kleinschreibung zu unterscheiden.
Mit dieser Aufgabe soll gezeigt werden, wie sich
- Auslöschungen (Erasures) ⇒ man kennt den Ort eines Fehlers,
- Zeichenfehler (Errors) ⇒ es ist nicht offensichtlich, was falsch und was richtig ist,
auf die Verständlichkeit eines Textes auswirken. Unser Text beinhaltet dabei auch die typisch deutschen Buchstaben „ä”, „ö”, „ü” und „ß” sowie Ziffern und Interpunktion. Außerdem wird zwischen Groß– und Kleinschreibung unterschieden.
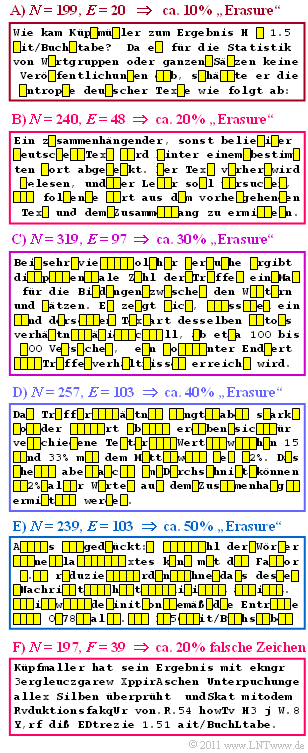
In der Abbildung ist dieser Text, der von Küpfmüllers Vorgehensweise handelt, in sechs Blöcke der Länge zwischen $N = 197$ bis $N = 319$ aufgeteilt. Beschrieben ist die Überprüfung seiner ersten Analyse auf völlig anderem Wege, die zum Ergebnis $H =1.51\ \rm bit/Zeichen$ führte.
- In den oberen fünf Blöcken erkennt man Erasures mit verschiedenen Auslöschwahrscheinlichkeiten zwischen 10% und 50%.
- Im letzten Block sind Zeichenfehler mit 20–prozentiger Verfälschungswahrscheinlichkeit eingefügt.
Der Einfluss solcher Zeichenfehler auf die Lesbarkeit eines Textes soll in der Teilaufgabe (4) verglichen werden mit dem zweiten (rot umrandeten) Block, für den die Wahrscheinlichkeit eines Erasures ebenfalls 20% beträgt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Nachrichtenquellen mit Gedächtnis.
- Bezug genommen wird insbesondere auf die beiden Seiten
Entropieabschätzung nach Küpfmüller sowie eine weitere Entropieabschätzung nachvon Küpfmüller.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Für die relative Redundanz einer Folge gilt mit dem Entscheidungsgehalt $H_0$ und der Entropie $H$ gilt:
- $$r = \frac{H_0 - H}{H_0}\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- 1. Der Symbolumfang bei Küpfmüllers Untersuchungen war M = 26, da er im Gegensatz zu Shannon das Leerzeichen zunächst nicht berücksichtigte. Bei dem vorgegebenen deutschen Text dieser Aufgabe ist der Symbolumfang deutlich größer,
- da hier auch die typisch deutschen Zeichen „ä”, „ö”, „ü” und „ß” vorkommen,
- zwischen Klein– und Großschreibung unterschieden wird,
- und zudem noch Ziffern und Interpunktionszeichen hinzukommen.
- 2. Mit dem Entscheidungsgehalt H0 = log2 (31) ≈ 4.7 und der Entropie H = 1.3 (jeweils mit der Einheit bit/Zeichen) erhält man für die relative Redundanz:
- $$r = \frac{H_0 - H}{H_0}= \frac{4.7 - 1.3}{4.7}\underline {\hspace{0.1cm}\approx 72.3\,\%}\hspace{0.05cm}.$$
- 3. Richtig ist nur der erste Lösungsvorschlag. Laut Küpfmüller benötigt man nur 1.3 Binärzeichen pro Quellenzeichen. Bei einer Datei der Länge N würden also 1.3 · N Binärsymbole ausreichen, allerdings nur dann, wenn
- die Quellensymbolfolge unendlich lang ist (N → ∞), und
- diese bestmöglich codiert ist.
- Dagegen besagt Küpfmüllers Ergebnis und die in der Teilaufgabe (b) errechnete relative Redundanz von mehr als 70% nicht, dass ein Leser den Text noch verstehen kann, wenn 70% der Zeichen ausgelöscht sind. Ein solcher Text
- ist nie unendlich lang,
- noch wurde er vorher optimal codiert.
- 4. Richtig ist Aussage 2. Testen Sie es selbst: Der zweite Block der Grafik auf der Angabenseite ist leichter zu entschlüsseln als der letzte Block, weil man weiß, wo es Fehler gibt. Wenn Sie es weiter versuchen wollen: Für den unteren Block wurde genau die gleiche Zeichenfehlerfolge wie für Block 2 verwendet, das heißt, Fehler gibt es bei den Zeichen 6, 35, 37, usw..
- Abschließend soll noch der Originaltext angegeben werden, der auf der Angabenseite nur durch Auslöschungen (Erasures) oder echte Zeichenfehler verfälscht wiedergegeben ist.