Aufgaben:Aufgabe 2.6Z: Nochmals zum Huffman–Code

• Zurück zum Buch

Der Algorithmus von David Albert Huffman realisiert eine Entropiecodierung mit folgenden Eigenschaften:

• Der entstehende Binärcode ist präfixfrei und somit in einfacher Weise (und sofort) decodierbar.

• Der Code führt bei gedächtnisloser Quelle zur kleinstmöglichen mittleren Codewortlänge $L_{\rm M}$.

• $L_{\rm M}$ ist aber nie kleiner als die Quellenentropie $H$. Diese beiden Größen sind allein aus den $M$ Symbolwahrscheinlichkeiten berechenbar.

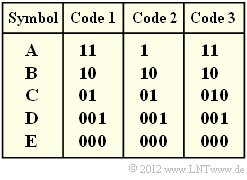
Vorausgesetzt wird für diese Aufgabe eine gedächtnislose Quelle mit dem Symbolumfang $M = 5$ und dem Alphabet $\{$A, B, C, D, E$\}$. In obiger Grafik sind drei Codes vorgegeben. Sie sollen entscheiden, welche dieser Codes durch Anwendung des Huffman–Algorithmus entstanden sind (oder sein könnten).

Hinweise:

• Die Aufgabe gehört zum Kapitel Entropiecodierung nach Huffman.
• Weitere Informationen zum Huffman–Algorithmus finden Sie auch im Angabenblatt zur Aufgabe 2.6.
• Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das Interaktionsmodul Shannon–Fano– und Huffman–Codierung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche Codes könnten entsprechend Huffman für $p_{\rm A} = p_{\rm B} = p_{\rm C} = 0.3$ und $p_{\rm D} = p_{\rm E} = 0.05$ entstanden sein?

	$\text{Code 1}$,
	$\text{Code 2}$,
	$\text{Code 3}$.

2

Wie stehen mittlere Codewortlänge $L_{\rm M}$ und Entropie $H$ bei den gegebenen Wahrscheinlichkeiten in Relation?

	$L_{\rm M} < H$,
	$L_{\rm M} \ge H$,
	$L_{\rm M} > H$.

3

Betrachten Sie $\text{Code 1}$. Mit welchen Symbolwahrscheinlichkeiten würde $L_{\rm M} = H$ gelten?

$\ p_{\rm A} \ = \ $

$\ p_{\rm B} \ = \ $

$\ p_{\rm C} \ = \ $

$\ p_{\rm D} \ = \ $

$\ p_{\rm E} \ = \ $

4

Die in der Teilaufgabe (3) berechneten Wahrscheinlichkeiten gelten weiter. Die mittlere Codewortlänge wird aber nun für eine Folge der Länge $N = 40$ ermittelt  ⇒  $L_{\rm M}'$. Was ist möglich?

	$L_{\rm M}' < L_{\rm M}$,
	$L_{\rm M}' = L_{\rm M}$,
	$L_{\rm M}' > L_{\rm M}$.

5

Welcher Code könnte überhaupt ein Huffman–Code sein?

	$\text{Code 1}$,
	$\text{Code 2}$,
	$\text{Code 3}$.

Musterlösung

Musterlösung

1.  Die Grafik zeigt die Konstruktion des Huffman–Codes mittels Baumdiagramm. Mit der Zuordnung rot → 1 und blau → 0 kommt man zu folgendem Code A → 11, B → 10, C → 01, D → 001, E → 000. Richtig ist der Lösungsvorschlag 1.

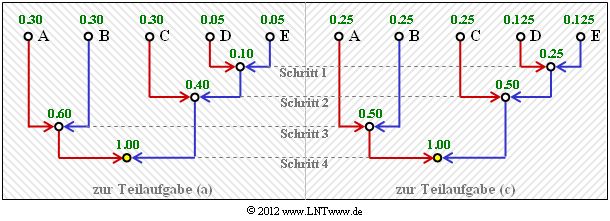
Die linke Grafik gilt für die Wahrscheinlichkeiten gemäß Teilaufgabe (a). Das rechte Diagramm gehört zur Teilaufgabe (3) mit etwas anderen Wahrscheinlichkeiten. Es liefert den genau gleichen Code.

b)  Nach dem Quellencodierungstheorem gilt stets L_M ≥ H. Voraussetzung für L_M = H ist allerdings, dass alle Symbolwahrscheinlichkeiten in der Form 2^–k (k = 1, 2, 3, ...) dargestellt werden können. Richtig ist demnach Lösungsvorschlag 3, wie auch die folgende Rechnung (mit „log₂”  ⇒  „ld”) zeigt:

$$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (0.3 + 0.3 + 0.3) \cdot 2 + (0.05 + 0.05) \cdot 3 = 2.1\,{\rm bit/Quellensymbol}\hspace{0.05cm},\\ H \hspace{0.2cm} = \hspace{0.2cm} 3 \cdot 0.3 \cdot {\rm ld}\hspace{0.15cm}(1/0.3) + 2 \cdot 0.05 \cdot {\rm ld}\hspace{0.15cm}(1/0.05) \approx 2.0\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$

3.  A, B, C werden beim Code 1 durch 2 Bit dargestellt, E, F durch 3 Bit. Damit erhält man für

• die mittlere Codewortlänge

$$L_{\rm M} = p_{\rm A}\cdot 2 + p_{\rm B}\cdot 2 + p_{\rm C}\cdot 2 + p_{\rm D}\cdot 3 + p_{\rm E}\cdot 3 \hspace{0.05cm},$$

• für die Quellenentropie:

$$H = p_{\rm A}\cdot {\rm ld}\hspace{0.15cm}\frac{1}{p_{\rm A}} + p_{\rm B}\cdot {\rm ld}\hspace{0.15cm}\frac{1}{p_{\rm B}} + p_{\rm C}\cdot {\rm ld}\hspace{0.15cm}\frac{1}{p_{\rm C}} + p_{\rm D}\cdot {\rm ld}\hspace{0.15cm}\frac{1}{p_{\rm D}} + p_{\rm E}\cdot {\rm ld}\hspace{0.15cm}\frac{1}{p_{\rm E}} \hspace{0.05cm}.$$

Durch Vergleich aller Terme kommt man zum Ergebnis:

$$p_{\rm A}= p_{\rm B}= p_{\rm C}\hspace{0.15cm}\underline{= 0.25} \hspace{0.05cm}, \hspace{0.2cm}p_{\rm D}= p_{\rm E}\hspace{0.15cm}\underline{= 0.125}$$

$$\Rightarrow\hspace{0.3cm} L_{\rm M} = H = 2.25\,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$

Man erkennt: Mit diesen „günstigeren” Wahrscheinlichkeiten ergibt sich sogar eine größere mittlere Codewortlänge. Die Gleichheit (L_M = H) ist allein auf die nun größere Quellenentropie zurückzuführen.

4.  Beispielsweise liefert eine (von vielen) Simulationen mit den Wahrscheinlichkeiten gemäß der Teilaufgabe (c) die Folge EBDCCBDABEBABCCCCCBCAABECAACCBAABBBCDCAB (mit <nobr>N = 40 Zeichen).</nobr> Damit ergibt sich:

$$L_{\rm M}' = ( 34 \cdot 2 + 6 \cdot 3)/50 = 2.15\,{\rm bit/Quellensymbol} \hspace{0.05cm},$$

also ein kleinerer Wert als für die unendlich lange Folge (L_M = 2.25 bit/Quellensymbol). Bei anderem Startwert des Zufallsgenerators ist aber auch L′_M ≥ L_M möglich. Alle Aussagen sind zutreffend.

5.  Richtig ist nur der Lösungsvorschlag 1.

• Code 1 ist ein Huffman–Code, wie schon in den vorherigen Teilaufgaben gezeigt wurde. Dies gilt zwar nicht für alle Symbolwahrscheinlichkeiten, aber zumindest für die Parametersätze gemäß den Teilaufgaben (a) und (c).

• Code 2 ist kein Huffman–Code, da ein solcher stets präfixfrei sein müsste. Die Präfixfreiheit ist hier aber nicht gegeben, da 0 der Beginn des Codewortes 01 ist.

• Code 3 ist ebenfalls kein Huffman–Code, da er eine um p_C (Wahrscheinlichkeit von C) größere mittlere Codewortlänge aufweist als erforderlich (Code 1). Er ist somit nicht optimal: Es gibt keine Symbolwahrscheinlichkeiten p_A, ... , p_E, die es rechtfertigen würden, das Symbol C mit 010 anstelle von 01 zu codieren.