Aufgaben:Aufgabe 2.12: Run–Length Coding & RLLC: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 2.13 Run–Length Coding & RLLC nach 2.12 Run–Length Coding & RLLC) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2474__Inf_A_2_13_neu.png|right|]] | + | [[Datei:P_ID2474__Inf_A_2_13_neu.png|right|Tabelle zu Run–Length Coding]] |
| − | Wir betrachten eine Binärquelle mit dem Symbolvorrat <b>A</b> und <b>B</b>, wobei <b>B</b> nur sehr selten auftritt. | + | Wir betrachten eine Binärquelle mit dem Symbolvorrat <b>A</b> und <b>B</b>, wobei <b>B</b> allerdings nur sehr selten auftritt. |
| − | + | * Ohne Quellencodierung würde man pro Quellensymbol genau ein Bit benötigen, und dementsprechend würde bei einer Quellensymbolfolge der Länge $N$ für die Codebit folge folge ebenfalls $N_\text{Bit} = N$gelten. | |
| + | * Entropiecodierung macht hier ohne weitere Maßnahme (Zusammenfassen mehrerer Symbole zu einem Tupel) wegen der ungünstigen Symbolwahrscheinlichkeiten wenig Sinn. | ||
| + | * Abhilfe schafft [[Informationstheorie/Weitere_Quellencodierverfahren#Laufl.C3.A4ngencodierung_.E2.80.93_Run.E2.80.93Length_Coding|Run-Length Coding]] (RLC), das unter dem genannten Link im Theorieteil beschrieben ist. Zum Beispiel ergibt sich für die Quellensymbolfolge: '''ABAABAAAABBAAB''' ... die entsprechende Ausgabe von ''Run–Lenght Coding'': ''' 2; 3; 5; 1; 3;''' ... | ||
| + | * Natürlich muss man die Längen $L_1 = 2$, $L_2 = 3$, ... der einzelnen, jeweils durch <b>B</b> getrennten Substrings vor der Übertragung binär darstellen. Verwendet man für alle $L_i$ jeweils $D = 3$ (Bit), so erhält man die RLC–Binärfolge '''010′011′101′001′011′'''... | ||
| − | + | Die Grafik zeigt das das zu analysierende RLC–Ergebnis. In Spalte 2 und 3 sind die Substringlängen $L_i$ binär bzw. dezimal angegeben und in Spalte 4 in kumulierter Form (Werte von Spalte 3 aufsummiert). | |
| − | + | Ein Problem von ''Run-Length Coding'' (RLC) ist der unbegrenzte Wertebereich der Größen $L_i$. Mit $D = 3$ kann kein Wert $L_i > 7$ dargestellt werden und mit $D = 2$ lautet die Beschränkung $1 \le L_i \le 3$. | |
| − | + | Das Problem umgeht man mit <i>Run–Length Limited Coding</i> (RLLC). Ist ein Wert $L_i \ge 2^D$, so ersetzt man $L_i$ durch ein Sonderzeichen <b>S</b> und die Differenz $L_i - 2^D +1$. Beim RLLC–Decoder wird dieses Sonderzeichen <b>S</b> wieder expandiert. | |
| − | : | + | {{GraueBox| |
| + | TEXT='''RLLC–Beispiel 2''': Wir gehen wieder von obiger Folge und dem Parameter $D = 2$ aus: | ||
| + | * Quellensymbolfolge: '''ABAABAAAABBAAB''' ... | ||
| + | * RLC–Dezimalfolge: '''2; 3; 5; 1; 3;''' ... | ||
| + | * RLLC–Dezimalfolge: '''2; 3;'''<font color="#cc0000"><span style="font-weight: bold;"> S;</span></font>'''2; 1; 3;''' ... | ||
| + | * RLLC–Binärfolge: '''01′11′''' <font color="#cc0000"><span style="font-weight: bold;">00′</span></font>'''10′01′11′'''... | ||
| − | :* | + | Man erkennt: |
| + | *Das Sonderzeichen <b>S</b> ist hier als <b>00</b> binär–codiert. Dies ist nur ein Beispiel – es muss nicht so sein. | ||
| + | *Da mit $D = 2$ für alle echten RLC–Werte $1 \le L_i \le 3$ gilt, erkennt der Decoder das Sonderzeichen '''00'''. | ||
| + | *Er ersetzt dieses wieder durch $2^D -1$ (im Beispiel drei) <b>A</b>–Symbole.}} | ||
| − | |||
| − | :* | + | ''Hinweise:'' |
| − | + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Weitere_Quellencodierverfahren|Weitere Quellencodierverfahren]]. | |
| − | + | *Insbesondere wird Bezug genommen auf die Seite [[Informationstheorie/Weitere_Quellencodierverfahren#Laufl.C3.A4ngencodierung_.E2.80.93_Run.E2.80.93Length_Coding|Lauflängencodierung – Run-Length Coding]]. | |
| − | + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Zeile 44: | Zeile 39: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wieviele Bit würde man <i>ohne Quellencodierung</i> benötigen, also mit der Zuordnung <b>A</b> → <b>0</b> und <b>B</b> | + | {Wieviele Bit würde man <i>ohne Quellencodierung</i> benötigen, also mit der Zuordnung <b>A</b> → <b>0</b> und <b>B</b> → <b>1</b>? |
|type="{}"} | |type="{}"} | ||
| − | + | $\text{ohne Codierung:} \ N_\text{Bit} \ = \ $ { 1250 3% } | |
{Wie groß ist die relative Häufigkeit des Symbols <b>B</b>? | {Wie groß ist die relative Häufigkeit des Symbols <b>B</b>? | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $h_{\rm B}\ = \ $ { 0.02 3% } |
| − | {Wie viele Bit benötigt man für <i>Run–Length Coding</i> (RLC) entsprechend der angegebenen Tabelle? | + | {Wie viele Bit benötigt man für <i>Run–Length Coding</i> (RLC) entsprechend der angegebenen Tabelle mit 8 Bit–Codeworten ? |
|type="{}"} | |type="{}"} | ||
| − | $RLC | + | $\text{RLC mit } D = 8\text{:} \ N_\text{Bit} \ = \ $ { 200 3% } |
| Zeile 67: | Zeile 62: | ||
{Wie viele Bit benötigt man mit <i>Run–Length Limited Coding</i> (RLLC) mit 7 Bit pro Codewort? | {Wie viele Bit benötigt man mit <i>Run–Length Limited Coding</i> (RLLC) mit 7 Bit pro Codewort? | ||
|type="{}"} | |type="{}"} | ||
| − | $RLLC | + | $\text{RLLC mit } D = 7\text{:} \ N_\text{Bit} \ = \ $ { 182 3% } |
{Wie viele Bit benötigt man mit <i>Run–Length Limited Coding</i> (RLLC) mit 6 Bit pro Codewort? | {Wie viele Bit benötigt man mit <i>Run–Length Limited Coding</i> (RLLC) mit 6 Bit pro Codewort? | ||
|type="{}"} | |type="{}"} | ||
| − | $RLLC | + | $\text{RLLC mit } D = 6\text{:} \ N_\text{Bit} \ = \ ${ 204 3% } |
Version vom 27. Mai 2017, 16:09 Uhr
Wir betrachten eine Binärquelle mit dem Symbolvorrat A und B, wobei B allerdings nur sehr selten auftritt.
- Ohne Quellencodierung würde man pro Quellensymbol genau ein Bit benötigen, und dementsprechend würde bei einer Quellensymbolfolge der Länge $N$ für die Codebit folge folge ebenfalls $N_\text{Bit} = N$gelten.
- Entropiecodierung macht hier ohne weitere Maßnahme (Zusammenfassen mehrerer Symbole zu einem Tupel) wegen der ungünstigen Symbolwahrscheinlichkeiten wenig Sinn.
- Abhilfe schafft Run-Length Coding (RLC), das unter dem genannten Link im Theorieteil beschrieben ist. Zum Beispiel ergibt sich für die Quellensymbolfolge: ABAABAAAABBAAB ... die entsprechende Ausgabe von Run–Lenght Coding: 2; 3; 5; 1; 3; ...
- Natürlich muss man die Längen $L_1 = 2$, $L_2 = 3$, ... der einzelnen, jeweils durch B getrennten Substrings vor der Übertragung binär darstellen. Verwendet man für alle $L_i$ jeweils $D = 3$ (Bit), so erhält man die RLC–Binärfolge 010′011′101′001′011′...
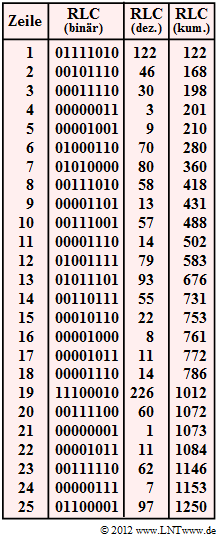
Die Grafik zeigt das das zu analysierende RLC–Ergebnis. In Spalte 2 und 3 sind die Substringlängen $L_i$ binär bzw. dezimal angegeben und in Spalte 4 in kumulierter Form (Werte von Spalte 3 aufsummiert).
Ein Problem von Run-Length Coding (RLC) ist der unbegrenzte Wertebereich der Größen $L_i$. Mit $D = 3$ kann kein Wert $L_i > 7$ dargestellt werden und mit $D = 2$ lautet die Beschränkung $1 \le L_i \le 3$.
Das Problem umgeht man mit Run–Length Limited Coding (RLLC). Ist ein Wert $L_i \ge 2^D$, so ersetzt man $L_i$ durch ein Sonderzeichen S und die Differenz $L_i - 2^D +1$. Beim RLLC–Decoder wird dieses Sonderzeichen S wieder expandiert.
RLLC–Beispiel 2: Wir gehen wieder von obiger Folge und dem Parameter $D = 2$ aus:
- Quellensymbolfolge: ABAABAAAABBAAB ...
- RLC–Dezimalfolge: 2; 3; 5; 1; 3; ...
- RLLC–Dezimalfolge: 2; 3; S;2; 1; 3; ...
- RLLC–Binärfolge: 01′11′ 00′10′01′11′...
Man erkennt:
- Das Sonderzeichen S ist hier als 00 binär–codiert. Dies ist nur ein Beispiel – es muss nicht so sein.
- Da mit $D = 2$ für alle echten RLC–Werte $1 \le L_i \le 3$ gilt, erkennt der Decoder das Sonderzeichen 00.
- Er ersetzt dieses wieder durch $2^D -1$ (im Beispiel drei) A–Symbole.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Quellencodierverfahren.
- Insbesondere wird Bezug genommen auf die Seite Lauflängencodierung – Run-Length Coding.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
2. Die gesamte Symbolfolge der Länge N = 1250 beinhaltet NB = 25 Symbole B und NA = 1225 Symbole A. Damit gilt für die relative Häufigkeit von B:
- $$h_{\rm B} = \frac{N_{\rm B}}{N} = \frac{25}{1250} \hspace{0.15cm}\underline{= 0.02} = 2\%\hspace{0.05cm}. $$
3. Wir betrachten nun Run–Length Coding (RLC), wobei jeder Abstand zwischen zwei B–Symbolen mit 8 Bit dargestellt wird (D = 8). Damit ergibt sich mit NB = 25:
- $$N_{\rm Bit} = N_{\rm B} \cdot 8 \hspace{0.15cm}\underline{= 200} \hspace{0.05cm}.$$
4. Run–Length Coding mit 7 Bit pro Codewort erlaubt für Li nur Werte zwischen 0 und 127. Der Eintrag „226” in Zeile 19 ist aber größer ⇒ NEIN.
5. Auch bei Run–Length Limited Coding (RLLC) sind für die „echten” Abstände Li mit D = 7 nur Werte zwischen 1 und 27 – 1 = 127 zulässig. Der Eintrag „226” in Zeile 19 wird bei RLLC ersetzt durch
- Zeile 19a: S = 0000000 ⇒ Sonderzeichen, steht für „+ 127”,
- Zeile 19b: 1100011 ⇒ Dezimal 99.
Damit erhält man insgesamt 26 Worte zu je 7 Bit:
- $$N_{\rm Bit} = 26 \cdot 7 \hspace{0.15cm}\underline{= 182} \hspace{0.05cm}.$$
6. Nun müssen bei RLLC gegenüber RLC (siehe Tabelle) folgende Änderungen vorgenommen werden:
- Zeile 1: 122 = 1 · 63 + 59 (ein Wort mehr),
- Zeile 6: 70 = 1 · 63 + 7 (ein Wort mehr),
- Zeile 7: 80 = 1 · 63 + 17 (ein Wort mehr),
- Zeile 12: 79 = 1 · 63 + 18 (ein Wort mehr),
- Zeile 13: 93 = 1 · 63 + 30 (ein Wort mehr),
- Zeile 19: 226 = 3 · 63 + 37 (drei Worte mehr),
- Zeile 25: 97 = 1 · 63 + 34 (ein Wort mehr).
Damit erhält man insgesamt 34 Worte zu je 6 Bit:
- $$N_{\rm Bit} = 34 \cdot 6 \hspace{0.15cm}\underline{= 204} \hspace{0.05cm},$$
also ein schlechteres Ergebnis als mit 7 Bit gemäß Teilaufgabe (5).