Aufgaben:Aufgabe 3.7: Einige Entropieberechnungen: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2766__Inf_A_3_6.png|right|]] | + | [[Datei:P_ID2766__Inf_A_3_6.png|right|Schaubild der Entropien und der Information]] |
Wir betrachten die beiden Zufallsgrößen $XY$ und $UV$ mit den folgenden 2D-Wahrscheinlichkeitsfunktionen: | Wir betrachten die beiden Zufallsgrößen $XY$ und $UV$ mit den folgenden 2D-Wahrscheinlichkeitsfunktionen: | ||
| − | + | :$$P_{XY}(X, Y) = \begin{pmatrix} 0.18 & 0.16\\ 0.02 & 0.64 \end{pmatrix}\hspace{0.05cm} \hspace{0.05cm}$$ | |
| − | $$P_{XY}(X, Y) = \begin{pmatrix} 0.18 & 0.16\\ 0.02 & 0.64 \end{pmatrix}\hspace{0.05cm} \hspace{0.05cm}$$ | + | :$$P_{UV}(U, V) \hspace{0.05cm}= \begin{pmatrix} 0.068 & 0.132\\ 0.272 & 0.528 \end{pmatrix}\hspace{0.05cm}$$ |
| − | |||
| − | $$P_{UV}(U, V) \hspace{0.05cm}= \begin{pmatrix} 0.068 & 0.132\\ 0.272 & 0.528 \end{pmatrix}\hspace{0.05cm}$$ | ||
Für die Zufallsgröße $XY$sollen in dieser Aufgabe berechnet werden: | Für die Zufallsgröße $XY$sollen in dieser Aufgabe berechnet werden: | ||
| − | + | * die Verbundentropie (englisch: ''Joint Entropy''): | |
| − | + | :$$H(XY) = -{\rm E}[\log_2 P_{ XY }( X,Y)],$$ | |
| − | + | * die beiden Einzelentropien: | |
| − | $H(XY) = -E[log_2 P_{ XY }( X,Y)]$ | + | :$$H(X) = -{\rm E}[\log_2 P_X( X)],$$ |
| − | + | :$$H(Y) = -{\rm E}[\log_2 P_Y( Y)].$$ | |
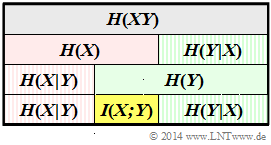
| − | + | Daraus lassen sich entsprechend dem obigen Schema – dargestellt für die Zufallsgröße $XY$ – auch folgende Beschreibungsgrößen sehr einfach bestimmen: | |
| − | $$H(X) = -E[log_2 P_X( X)]$$ | + | * die bedingten Entropien (englisch: ''Conditional Entropies''): |
| − | $$H(Y) = -E[log_2 P_Y( Y)]$$ | + | :$$H(X \hspace{0.05cm}|\hspace{0.05cm} Y) = -{\rm E}[\log_2 P_{ X \hspace{0.05cm}|\hspace{0.05cm} }( X \hspace{0.05cm}|\hspace{0.05cm} Y)],$$ |
| − | Daraus lassen sich entsprechend dem obigen Schema – dargestellt für die Zufallsgröße $XY$ – | + | :$$H(Y \hspace{0.05cm}|\hspace{0.05cm} Y) = -{\rm E}[\log_2 P_{ Y \hspace{0.05cm}|\hspace{0.05cm} X }( Y \hspace{0.05cm}|\hspace{0.05cm} X)],$$ |
| − | + | * die Transinformation (englisch: Mutual Information) zwischen $X$ und $Y$: | |
| − | + | :$$I(X;Y) = {\rm E}[\log_2 \frac{P_{ XY }(X,Y)}{P_X(X) \cdot P_Y(Y)}].$$ | |
| − | |||
| − | $H(X \ | ||
| − | |||
| − | $H(Y \ | ||
| − | |||
| − | |||
| − | |||
| − | $I(X;Y) = E [log_2 \frac{P_{ XY }(X,Y)}{P_X(X) | ||
Abschließend sind qualitative Aussagen hinsichtlich der zweiten Zufallsgröße $UV$ zu verifizieren. | Abschließend sind qualitative Aussagen hinsichtlich der zweiten Zufallsgröße $UV$ zu verifizieren. | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/ | + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen|Verschiedene Entropien zweidimensionaler Zufallsgrößen]]. |
| − | *Insbesondere wird Bezug genommen auf die | + | *Insbesondere wird Bezug genommen auf die Seiten [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Bedingte_Wahrscheinlichkeit_und_bedingte_Entropie|Bedingte Wahrscheinlichkeit und bedingte Entropie]] sowie [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Transinformation_zwischen_zwei_Zufallsgr.C3.B6.C3.9Fen|Transinformation zwischen zwei Zufallsgrößen]]. |
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| − | |||
| − | |||
| − | |||
Version vom 1. Juni 2017, 10:52 Uhr
Wir betrachten die beiden Zufallsgrößen $XY$ und $UV$ mit den folgenden 2D-Wahrscheinlichkeitsfunktionen:
- $$P_{XY}(X, Y) = \begin{pmatrix} 0.18 & 0.16\\ 0.02 & 0.64 \end{pmatrix}\hspace{0.05cm} \hspace{0.05cm}$$
- $$P_{UV}(U, V) \hspace{0.05cm}= \begin{pmatrix} 0.068 & 0.132\\ 0.272 & 0.528 \end{pmatrix}\hspace{0.05cm}$$
Für die Zufallsgröße $XY$sollen in dieser Aufgabe berechnet werden:
- die Verbundentropie (englisch: Joint Entropy):
- $$H(XY) = -{\rm E}[\log_2 P_{ XY }( X,Y)],$$
- die beiden Einzelentropien:
- $$H(X) = -{\rm E}[\log_2 P_X( X)],$$
- $$H(Y) = -{\rm E}[\log_2 P_Y( Y)].$$
Daraus lassen sich entsprechend dem obigen Schema – dargestellt für die Zufallsgröße $XY$ – auch folgende Beschreibungsgrößen sehr einfach bestimmen:
- die bedingten Entropien (englisch: Conditional Entropies):
- $$H(X \hspace{0.05cm}|\hspace{0.05cm} Y) = -{\rm E}[\log_2 P_{ X \hspace{0.05cm}|\hspace{0.05cm} }( X \hspace{0.05cm}|\hspace{0.05cm} Y)],$$
- $$H(Y \hspace{0.05cm}|\hspace{0.05cm} Y) = -{\rm E}[\log_2 P_{ Y \hspace{0.05cm}|\hspace{0.05cm} X }( Y \hspace{0.05cm}|\hspace{0.05cm} X)],$$
- die Transinformation (englisch: Mutual Information) zwischen $X$ und $Y$:
- $$I(X;Y) = {\rm E}[\log_2 \frac{P_{ XY }(X,Y)}{P_X(X) \cdot P_Y(Y)}].$$
Abschließend sind qualitative Aussagen hinsichtlich der zweiten Zufallsgröße $UV$ zu verifizieren.
Hinweise:
- Die Aufgabe gehört zum Kapitel Verschiedene Entropien zweidimensionaler Zufallsgrößen.
- Insbesondere wird Bezug genommen auf die Seiten Bedingte Wahrscheinlichkeit und bedingte Entropie sowie Transinformation zwischen zwei Zufallsgrößen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
1. Aus der gegebenen Verbundwahrscheinlichkeit erhält man
$$H(XY) = 0,18 . log_2 \frac{1}{0,18} + 0,16 . log_2 \frac{1}{0,16}$$
$$+ 0,02 . log_2 \frac{1}{0,02} + 0,64 . log_2 \frac{1}{0,64} = 1,393 (bit)$$
2. Die 1D–Wahrscheinlichkeitsfunktionen lauten $P_X(X) = [0.2, 0.8]$ und $P_Y(Y) = [0.34, 0.66]$. Daraus folgt:
$H(X) = 0,2 . log_2 \frac{1}{0.2} + 0,8 . log_2 \frac{1}{0,8} = 0.722 (bit)$
$H(Y) = 0,34 . log_2 \frac{1}{0.34} + 0,66 . log_2 \frac{1}{0,66} = 0.925 (bit)$
3. Aus der $Grafik$ auf der Angabenseite erkennt man den Zusammenhang:
$$I(X;Y) = H(X) + H(Y) - H(XY) = $$ $$ = 0.722 (bit) + 0.925 (bit)- 1.393 (bit) = 0.254 (bit)$$
4. Ebenso gilt entsprechend der $Grafik$ auf der Angabenseite:
$$H(X \mid Y) = H(XY) - H(Y) = 1.393 - 0.925 = 0.468 (bit)$$ $$H(Y \mid X) = H(XY) - H(X) = 1.393 - 0.722 = 0.671 (bit)$$
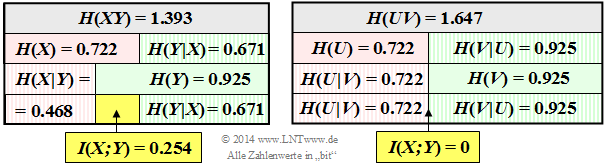
Die linke Grafik fasst die Ergebnisse der Teilaufgaben (a), ... , (d) maßstabsgetreu zusammen. Grau hinterlegt ist die Verbundentropie und gelb die Transinformation. Eine rote Hinterlegung bezieht sich auf die Zufallsgröße $X$, eine grüne auf $Y$. Schraffierte Felder deuten auf eine bedingte Entropie hin.
Die rechte Grafik beschreibt den gleichen Sachverhalt für die Zufallsgröße $UV \Rightarrow$ Teilaufgabe (e).
5. Man erkennt die Gültigkeit von $P_{ UV } (.) = P_U (⋅) · P_V(⋅) \Rightarrow$ Transinformation $I(U; V) = 0$ daran, dass die zweite Zeile der $P_{ UV }$–Matrix sich von der ersten Zeile nur durch einen konstanten Faktor (4) unterscheidet. Richtig sind demzufolge die Aussagen 1, 2 und 4. Weiter ist zu erwähnen:
- Es ergeben sich die gleichen 1D–Wahrscheinlichkeitsfunktiionen wie für die Zufallsgröße $XY \Rightarrow P_U(U) = [0.2, 0.8]$ und $P_V(V) = [0.34, 0.66]$.
- Deshalb ist auch $H(U) = H(X) = 0.722$ bit und $H(V) = H(Y) = 0.925 bit$.
- Hier gilt aber nun für die Verbundentropie: $H(UV) = H(U) + H(V) ≠ H(XY)$.