Aufgaben:Aufgabe 2.1Z: ZSB-AM ohne/mit Träger: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID987__Mod_Z_2_1.png|right|]] | + | [[Datei:P_ID987__Mod_Z_2_1.png|right|frame|Die bei der Amplitudenmodulation beteiligten Signale]] |
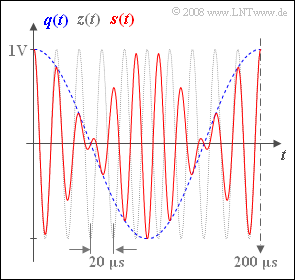
| − | Die Grafik zeigt mit dem roten Kurvenverlauf einen Ausschnitt des Sendesignals$s(t) = q(t) · z(t)$ | + | Die Grafik zeigt mit dem roten Kurvenverlauf einen Ausschnitt des Sendesignals $s(t) = q(t) · z(t)$ einer Zweiseitenband–Amplitudenmodulation (abgekürzt mit ZSB-AM) ohne Träger. Die Dauer des Zeitausschnitts beträgt $200$ μs. |
| − | Zusätzlich sind das Quellensignal (als blau–gestrichelte Kurve) | + | Zusätzlich sind in der Grafik eingetragen: |
| − | $$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N})$$ | + | *das Quellensignal (als blau–gestrichelte Kurve): |
| − | + | :$$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N}),$$ | |
| − | $$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})$$ | + | *das Trägersignal (grau–gepunkteter Verlauf): |
| − | + | :$$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})$$ | |
| − | Ab der Teilaufgabe | + | Ab der Teilaufgabe (4) wird die „ZSB–AM mit Träger” betrachtet. Dann gilt mit $A_{\rm T} = 2$ V: |
| − | $$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$ | + | :$$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$ |
| − | '' | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation|Zweiseitenband-Amplitudenmodulation]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seiten [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#Beschreibung_im_Zeitbereich|Beschreibung im Zeitbereich]] und [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#ZSB-Amplitudenmodulation_mit_Tr.C3.A4ger|ZSB-Amplitudenmodulation_mit_Träger]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
| + | |||
| + | ' | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Ermitteln Sie die Phasenwerte von Quellen– und Trägersignal | + | {Ermitteln Sie aus der Grafik die Phasenwerte von Quellen– und Trägersignal. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\phi_{\rm N} \ = \ $ { 0. } $\ \text{Grad}$ |
| − | $\ | + | $\phi_{\rm T} \ = \ $ { 0. } $\ \text{Grad}$ |
| − | { | + | {Welche Frequenz $f_{\rm N}$ besitzt das Nachrichtensignal $q(t)$ und welche Frequenz $f_{\rm T}$ das Trägersignal $z(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $f_{\rm N} \ = \ $ { 5 3% } $\ \text{kHz}$ |
| − | $ | + | $f_{\rm T} \ = \ $ { 50 3% } $\ \text{kHz}$ |
{Analysieren Sie die Nulldurchgänge von $s(t)$. Welche Aussagen treffen zu? | {Analysieren Sie die Nulldurchgänge von $s(t)$. Welche Aussagen treffen zu? | ||
| Zeile 34: | Zeile 40: | ||
+ Alle Nulldurchgänge von $z(t)$ bleiben in $s(t)$ erhalten. | + Alle Nulldurchgänge von $z(t)$ bleiben in $s(t)$ erhalten. | ||
+ Es gibt weitere Nullstellen, verursacht durch $q(t)$. | + Es gibt weitere Nullstellen, verursacht durch $q(t)$. | ||
| − | - Es gilt $s(t) = a(t) · cos(ω_T · t)$ mit $a(t) = |q(t)|$. | + | - Es gilt $s(t) = a(t) · \cos(ω_T · t)$ mit $a(t) = |q(t)|$. |
{Bestimmen Sie die Spektralfunktion $S(f)$ über die Faltung. Welche (positiven) Frequenzen $f_1$ und $f_2 > f_1$ sind im Signal enthalten? | {Bestimmen Sie die Spektralfunktion $S(f)$ über die Faltung. Welche (positiven) Frequenzen $f_1$ und $f_2 > f_1$ sind im Signal enthalten? | ||
|type="{}"} | |type="{}"} | ||
| − | $f_1$ | + | $f_1 \ = \ $ { 45 3% } $\ \text{kHz}$ |
| − | $f_2$ | + | $f_2\ = \ $ { 55 3% } $\ \text{kHz}$ |
| − | {Es gelte nun $ | + | {Es gelte nun $A_{\rm T} = 2$ V. Wie groß ist der Modulationsgrad $m$? |
|type="{}"} | |type="{}"} | ||
| − | $m$ | + | $m \ = \ $ { 0.5 3% } |
| − | {Welche der Aussagen treffen bei der „ZSB–AM mit Träger” und $ | + | {Welche der Aussagen treffen bei der „ZSB–AM mit Träger” und $A_{\rm T} = 2$ V zu? |
|type="[]"} | |type="[]"} | ||
| − | + $S(f)$ beinhaltet nun auch Diracfunktionen bei $ | + | + $S(f)$ beinhaltet nun auch Diracfunktionen bei $±f_{\rm T}$. |
| − | - Die Gewichte dieser Diraclinien sind jeweils 2 V. | + | - Die Gewichte dieser Diraclinien sind jeweils $2$ V. |
+ $q(t)$ ist in der Hüllkurve von $s(t)$ zu erkennen. | + $q(t)$ ist in der Hüllkurve von $s(t)$ zu erkennen. | ||
- Durch den zusätzlichen Trägeranteil bleibt die Leistung unverändert. | - Durch den zusätzlichen Trägeranteil bleibt die Leistung unverändert. | ||
Version vom 22. Juni 2017, 13:09 Uhr
Die Grafik zeigt mit dem roten Kurvenverlauf einen Ausschnitt des Sendesignals $s(t) = q(t) · z(t)$ einer Zweiseitenband–Amplitudenmodulation (abgekürzt mit ZSB-AM) ohne Träger. Die Dauer des Zeitausschnitts beträgt $200$ μs.
Zusätzlich sind in der Grafik eingetragen:
- das Quellensignal (als blau–gestrichelte Kurve):
- $$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N}),$$
- das Trägersignal (grau–gepunkteter Verlauf):
- $$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})$$
Ab der Teilaufgabe (4) wird die „ZSB–AM mit Träger” betrachtet. Dann gilt mit $A_{\rm T} = 2$ V:
- $$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweiseitenband-Amplitudenmodulation.
- Bezug genommen wird insbesondere auf die Seiten Beschreibung im Zeitbereich und ZSB-Amplitudenmodulation_mit_Träger.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
'
Fragebogen
Musterlösung
2.Aus der Grafik können für $q(t)$ und $z(t)$ die Periodendauern $200 μs$ bzw. $20 μs$ abgelesen werden. Daraus ergeben sich die Frequenzen zu $f_N = 5 kHz$ und $f_T = 50 kHz$.
3. Die Nullstellen von $z(t)$ bei $±5 μs$, $±15 μs$, $±25 μs$, usw. sind auch im Signal $s(t)$ vorhanden. Weitere Nullstellen von $s(t)$ - verursacht durch $q(t)$ – liegen bei $±50 μs$, $±150 μs$, $±250 μs$, usw.. Richtig sind somit die Aussagen 1 und 2. Die dritte Aussage trifft dagegen nicht zu, sondern es gilt:
$$ s(t) = a(t) \cdot \cos(\omega_{\rm T} t + \phi (t)) \hspace{0.05cm}.$$
Für $q(t) > 0$ ist die Phasenfunktion $ϕ(t) = 0$ und $s(t)$ ist gleichlaufend mit $z(t)$. Dagegen gilt für $q(t) < 0$: $ϕ(t) = π = 180°$. Bei den Nulldurchgängen von $q(t)$ weist das modulierte Signal $s(t)$ Phasensprünge auf.
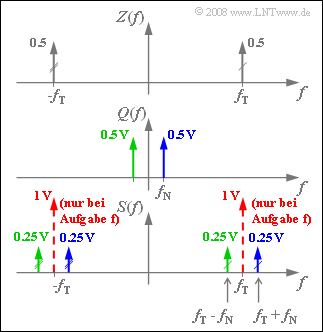
4.Das Spektrum $S(f)$ ergibt sich aus der Faltung der Spektralfunktionen $Z(f)$ und $Q(f)$, die jeweils aus nur zwei Diracfunktionen bestehen. Die Grafik zeigt das Ergebnis.
Die rot eingezeichneten Diracfunktionen gelten nur für die „ZSB–AM mit Träger” und beziehen sich auf die Teilaufgabe f). Die Faltung der beiden $Z(f)$–Diracfunktionen bei $f_T = 50 kHz$ mit $Q(f)$ führt zu den Diraclinien bei $f_T – f_N$ und $f_T + f_N$, jeweils mit Gewicht 0.5 · 0.5 V = 0.25 V.
Die gesuchten Werte sind somit $f_1 = 45 kHz$ und $f_2 = 55 kHz$. Die mit zwei Markierungsstrichen versehene Diracfunktion $0.5 · δ(f + f_T)$ führt zu zwei weiteren Diraclinien bei $–f_1$ und $–f_2$.
5.Der Modulationsgrad berechnet sich zu:
$$ m = \frac{q_{\rm max}}{A_{\rm T}} = \frac{A_{\rm N}}{A_{\rm T}} \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$
6.Gemäß der Skizze bei d) ergeben sich Diraclinien bei $±f_T$, beide mit dem Impulsgewicht $A_T/2 = 1 V$. Bei m ≤ 1 ist $q(t)$ in der Hüllkurve erkennbar und Hüllkurvendemodulation anwendbar. Allerdings muss diese einfachere Empfängervariante durch eine sehr viel größere Sendeleistung erkauft werden. In diesem Beispiel (m = 0.5) wird die Sendeleistung durch den Trägerzusatz verneunfacht. Richtig sind demzufolge die Lösungsvorschläge 1 und 3.