Aufgaben:Aufgabe 3.3Z: Kenngrößenbestimmung: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1085__Mod_Z_3_3.png|right|]] | + | [[Datei:P_ID1085__Mod_Z_3_3.png|right|frame|Spektrum des analytischen Signals]] |
Wir betrachten die Phasenmodulation der harmonischen Schwingung | Wir betrachten die Phasenmodulation der harmonischen Schwingung | ||
| − | $$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N}) \hspace{0.05cm},$$ | + | :$$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N}) \hspace{0.05cm},$$ |
| − | die bei Voraussetzung einer normierten Trägeramplitude ($ | + | die bei Voraussetzung einer normierten Trägeramplitude ($A_{\rm T} = 1$) zu folgendem Sendesignal führt: |
| − | $$ s(t) = \cos \left(\omega_{\rm T} \cdot t + K_{\rm PM} \cdot q(t) \right)\hspace{0.05cm}.$$ | + | :$$ s(t) = \cos \left(\omega_{\rm T} \cdot t + K_{\rm PM} \cdot q(t) \right)\hspace{0.05cm}.$$ |
| − | Das Spektrum des dazugehörigen analytischen Signals $s_{TP}(t)$ lautet allgemein: | + | Das Spektrum des dazugehörigen analytischen Signals $s_{\rm TP}(t)$ lautet allgemein: |
| − | $$S_{\rm TP}(f) = \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}(\phi_{\rm N}\hspace{0.05cm}+\hspace{0.05cm} 90^\circ) }\cdot \hspace{0.05cm} \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}$$ | + | :$$S_{\rm TP}(f) = \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}(\phi_{\rm N}\hspace{0.05cm}+\hspace{0.05cm} 90^\circ) }\cdot \hspace{0.05cm} \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}$$ |
| − | Hierbei bezeichnet man $η = K_{PM} · | + | Hierbei bezeichnet man $η = K_{\rm PM} · A_{\rm N}$ als den Modulationsindex. |
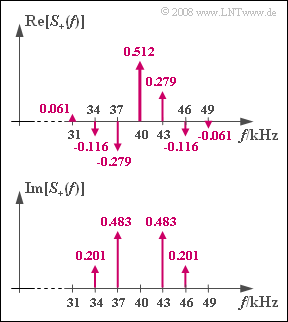
| − | In der Grafik ist das Spektrum $S_+(f)$ des analytischen Signals $s_+(t)$ getrennt nach Real- und Imaginärteil dargestellt. Aus diesem sollen die Kenngrößen $ | + | In der Grafik ist das Spektrum $S_+(f)$ des analytischen Signals $s_+(t)$ getrennt nach Real- und Imaginärteil dargestellt. Aus diesem sollen die Kenngrößen $f_{\rm T}$, $f_{\rm N}$, $ϕ_{\rm N}$ und $η$ ermittelt werden. |
| − | '' | + | |
| − | $${\rm J}_n (\eta) = \frac{2 \cdot (n-1)}{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm J}_{2} (\eta)= {2}/{\eta} \cdot {\rm J}_{1} (\eta) - {\rm J}_{0} (\eta) \hspace{0.05cm}.$$ | + | ''Hinweise:'' |
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Phasenmodulation_(PM)|Phasenmodulation]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Phasenmodulation_(PM)#.C3.84quivalentes_TP.E2.80.93Signal_bei_Phasenmodulation|Äquivalentes Tiefpass-Signal bei Phasenmodulation]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | *Zur Berechnung des Modulationsindex können Sie folgende Eigenschaft der Besselfunktion ausnutzen: | ||
| + | :$${\rm J}_n (\eta) = \frac{2 \cdot (n-1)}{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm J}_{2} (\eta)= {2}/{\eta} \cdot {\rm J}_{1} (\eta) - {\rm J}_{0} (\eta) \hspace{0.05cm}.$$ | ||
| Zeile 23: | Zeile 28: | ||
{Wie groß sind die Frequenzen $f_T$ und $f_N$? | {Wie groß sind die Frequenzen $f_T$ und $f_N$? | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $f_{\rm T} \ = \ $ { 40 3% } $\ \rm kHz$ |
| − | $ | + | $f_{\rm N} \ = \ $ { 3 3% } $\ \rm kHz$ |
| − | {Berechnen Sie den Betrag und die Phase von $S_{TP}(f = 3 kHz)$. | + | {Berechnen Sie den Betrag und die Phase von $S_{\rm TP}(f = 3 \ \rm kHz)$. |
|type="{}"} | |type="{}"} | ||
| − | $|S_{TP}(f = 3 kHz)|$ | + | $|S_{\rm TP}(f = 3 \ \rm kHz)| \ = \ $ { 0.558 3% } |
| − | $arc S_{TP}(f = 3 kHz)$ | + | $arc \ S_{\rm TP}(f = 3\ \rm kHz) \ = \ $ { 60 3% } $\ \rm Grad$ |
| − | {Berechnen Sie den Betrag und die Phase von $S_{TP}(f = 6 kHz)$. | + | {Berechnen Sie den Betrag und die Phase von $S_{\rm TP}(f = 6 \ \rm kHz)$. |
|type="{}"} | |type="{}"} | ||
| − | $|S_{TP}(f = 6 kHz)|$ | + | $|S_{\rm TP}(f = 6 \ \rm kHz)| \ = \ $ { 0.232 3% } |
| − | $arc S_{TP}(f = 6 kHz)$ | + | $arc \ S_{\rm TP}(f = 6\ \rm kHz) \ = \ $ { 120 3% } $\ \rm Grad$ |
| − | {Wie groß ist die Phase des Quellensignals? | + | {Wie groß ist die Phase des Quellensignals $q(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $ϕ_{\rm N} \ = \ $ { -30.9--29.1 } $\ \rm Grad$ |
| − | {Wie groß ist der Modulationsindex? | + | {Wie groß ist der Modulationsindex $η$? |
|type="{}"} | |type="{}"} | ||
| − | $η$ | + | $η \ = \ $ { 1.5 3% } |
Version vom 5. Juli 2017, 15:16 Uhr
Wir betrachten die Phasenmodulation der harmonischen Schwingung
- $$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N}) \hspace{0.05cm},$$
die bei Voraussetzung einer normierten Trägeramplitude ($A_{\rm T} = 1$) zu folgendem Sendesignal führt:
- $$ s(t) = \cos \left(\omega_{\rm T} \cdot t + K_{\rm PM} \cdot q(t) \right)\hspace{0.05cm}.$$
Das Spektrum des dazugehörigen analytischen Signals $s_{\rm TP}(t)$ lautet allgemein:
- $$S_{\rm TP}(f) = \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}(\phi_{\rm N}\hspace{0.05cm}+\hspace{0.05cm} 90^\circ) }\cdot \hspace{0.05cm} \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}$$
Hierbei bezeichnet man $η = K_{\rm PM} · A_{\rm N}$ als den Modulationsindex.
In der Grafik ist das Spektrum $S_+(f)$ des analytischen Signals $s_+(t)$ getrennt nach Real- und Imaginärteil dargestellt. Aus diesem sollen die Kenngrößen $f_{\rm T}$, $f_{\rm N}$, $ϕ_{\rm N}$ und $η$ ermittelt werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Phasenmodulation.
- Bezug genommen wird insbesondere auf die Seite Äquivalentes Tiefpass-Signal bei Phasenmodulation.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Zur Berechnung des Modulationsindex können Sie folgende Eigenschaft der Besselfunktion ausnutzen:
- $${\rm J}_n (\eta) = \frac{2 \cdot (n-1)}{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm J}_{2} (\eta)= {2}/{\eta} \cdot {\rm J}_{1} (\eta) - {\rm J}_{0} (\eta) \hspace{0.05cm}.$$
Fragebogen
Musterlösung
2. Unter Berücksichtigung von $S_{TP}(f = 3 kHz) = S_+(f = 43 kHz)$ gilt: $$|S_{\rm TP}(f = 3\,{\rm kHz})| = \sqrt{0.279^2 + 0.483^2} \hspace{0.15cm}\underline {= 0.558}\hspace{0.05cm},$$ $$ {\rm arc}\hspace{0.15cm} S_{\rm TP}(f = 3\,{\rm kHz}) = \arctan \frac{0.483}{0.279} = \arctan 1.732\hspace{0.15cm}\underline { = 60^\circ} \hspace{0.05cm}.$$
3. n analoger Weise zur Teilaufgabe b) erhält man für $6 kHz$: $$|S_{\rm TP}(f = 6\,{\rm kHz})| = \sqrt{(-0.116)^2 + 0.201^2} \hspace{0.15cm}\underline {= 0.232}\hspace{0.05cm},$$ $${\rm arc}\hspace{0.15cm} S_{\rm TP}(f = 6\,{\rm kHz}) = \arctan \frac{-0.116}{0.201} = 180^\circ - \arctan 1.732 \hspace{0.15cm}\underline {= 120^\circ} \hspace{0.05cm}.$$
4. Die Phase lautet für $n = 1$ (siehe Teilaufgabe b): $$ \phi_{\rm N} + 90^\circ = 60^\circ \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi_{\rm N} = -30^\circ\hspace{0.05cm}.$$ Die Überprüfung dieses Ergebnisses mit $n = 2$ liefert den gleichen Wert: $$ 2\cdot (\phi_{\rm N} + 90^\circ) = 120^\circ \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\phi_{\rm N} \hspace{0.15cm}\underline {= -30^\circ}\hspace{0.05cm}.$$
5. Die angegebene Gleichung kann wie folgt umgeformt werden: $$\eta = \frac{2 \cdot {\rm J}_{1}{(\eta)}}{{\rm J}_{0}(\eta) + {\rm J}_{2}(\eta)} \hspace{0.05cm}.$$ Mit $J_0(η) = 0.512$, $J_1(η) = 0.558$ und $J_2(η) = 0.232$ erhält man somit: $$ \eta = \frac{2 \cdot 0.558}{0.512 + 0.232}\hspace{0.15cm}\underline { = 1.5}\hspace{0.05cm}.$$