Aufgaben:Aufgabe 5.10: DMT–Verfahren bei DSL

• Zurück zum Buch

Bandbreitenorganisation bei DSL

Wir betrachten in dieser Aufgabe ein DSL–System (Digital Subscriber Line), das zur Modulation

• DMT (Discrete Multitone Transmission)
• mit $N = 512$ Stützstellen

verwendet wird. In diesem Zusammenhang werden die Träger auch als „Bins” bezeichnet. Für DSL ist festgelegt:

• Der Trägerabstand sei $f_0 = 4.3125\ \rm kHz$.
• Das Signal ist gleichanteilsfrei: $S(f = 0) = 0$.
• Der sogenannte Nyquist–Tone wird ebenfalls zu Null gesetzt: $S(256 · f_0) = 0$.

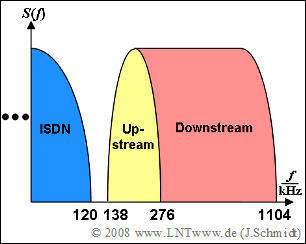
Die Grafik zeigt die Bandbreitenorganisation des betrachteten Systems für positive Frequenzen:

• Ein Übertragungsrahmen der DMT setzt sich wie bei OFDM aus der Kernsymboldauer $T$ und der Dauer $T_{\rm G}$ des zyklischen Präfixes zusammen. Dieses bestehe aus $N_{\rm G} = 32$ Abtastwerten.
• Zur Synchronisation zwischen Sender und Empfänger wird nach jeweils 68 Rahmen ein Synchronisationsrahmen gesendet, der keine Nutzdaten enthält.

Hinweise:

• Die Aufgabe gehört zum Kapitel Weitere OFDM–Anwendungen.
• Bezug genommen wird insbesondere auf die Seiten Eine Kurzbeschreibung von DSL sowie Unterschiede zwischen DMT und dem beschriebenen OFDM.
• Weitere Informationen zum Thema finden Sie im zweiten Kapitel: DSL – Digital Subscriber Line des LNTwww–Buchs Beispiele von Nachrichtensystemen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche der folgenden Aussagen ist richtig?

	Bei DSL handelt es sich um ein Bandpass–System.
	DSL wird im Basisband betrieben

2

Welche der folgenden Aussagen trifft auf das DMT–Zeitsignal zu?

	Das Zeitsignal ist rein reell.
	Das Zeitsignal ist rein imaginär.
	Das Zeitsignal ist komplex.

3

Wie viele Bins stehen für den Upstream und den Downstream zur Verfügung?

$N_{\rm Up} \ = \ $

$N_{\rm Down} \ = \ $

4

Geben Sie die Dauer $T$ des Kernsymbols an:

$T \ = \ $ $\ \rm μs$

5

Wie groß ist die Dauer $T_{\rm G}$ des Guard–Intervalls?

$T_{\rm G} \ = \ $ $\ \rm μs$

6

Welcher Wert ergibt sich somit für die Rahmendauer $T_{\rm R}$?

$T_{\rm R} \ = \ $ $\ \rm μs$

7

Geben Sie die Nutzbitrate des gezeigten Systems für den Downstream an, wenn für alle Träger BPSK verwendet wird:

$R_\text {B, Down} \ = \ $ $\ \rm kbit/s$

8

Die 198–te Stützstelle des (finiten) DMT–Spektrums sei mit $1 + 3 · {\rm j}$ belegt. Bestimmen Sie den Wert der 314–ten Stützstelle:

$\text{Re}(314 · f_0) \ = \ $

$\text{Im}(314 · f_0) \ = \ $

Musterlösung

Musterlösung

(1)  Richtig ist der Lösungsvorschlag 2:

• Bei DSL handelt es sich um ein Basisbandsystem.
• Im Unterschied dazu sind Mobilfunksysteme Bandpass–Systeme, die in entsprechend hohen Frequenzbereichen betrieben werden.
• Um diese ebenfalls in der üblichen Weise betrachten zu können, ist dazu eine (äquivalente) Tiefpass–Transformation notwendig.

(2)  Richtig ist der Lösungsvorschlag 1:

• Das Zeitsignal ist rein reell, da der Realteil des Spektrums gerade und der Imaginärteil ungerade ist.
• Diese Eigenschaft geht bei Bandpass–Systemen, die in das äquivalente Basisband transformiert werden müssen, durch das Abschneiden der negativen Frequenzen verloren. Das Zeitsignal wird dadurch komplex.

(3)  Die entsprechenden Bandbreiten für die Rechnung sind aus der Grafik ablesbar:

$$N_{{\rm{Up}}} = \frac{{276\,\,{\rm kHz}} -{138\,\,{\rm kHz}}} {{4.3125\,\,{\rm kHz}}}\hspace{0.15cm}\underline {= 32},$$

$$N_{{\rm{Down}}} = \frac{{1104\,\,{\rm kHz}} -{276\,\,{\rm kHz}}} {{4.3125\,\,{\rm kHz}}}\hspace{0.15cm}\underline {= 192}.$$

(4)  Die Kernsymboldauer ist der Kehrwert der Grundfrequenz:

$$T = \frac{1} {f_0}= \frac{1} {{4.3125\,\,{\rm kHz}}} \hspace{0.15cm}\underline {\approx 232 \,\,{\rm \mu s}}.$$

(5)  Daraus ergibt sich für die Dauer des Guard–Intervalls:

$$T_{\rm G} = \frac{N_{\rm G}} {N} \cdot T = \frac{32} {512} \cdot 232 \,\,{\rm \mu s} \hspace{0.15cm}\underline {\approx 14 \,\,{\rm \mu s}}.$$

(6)  Ein Rahmen setzt sich aus Kernsymbol und zyklischem Präfix zusammen:

$$T_{\rm R} = T + T_{\rm G}\hspace{0.15cm}\underline { ≈ 246 ß ßrm μs}$$.

(7)  Mit den Parametern $N_{Down} = 192$, $T_R ≈ 246 μs$ und M = 2 erhält man:

$$R_{\rm B,\, Down} = \frac{192 \cdot {{\rm{log}_2}(2)}}{246 \,\,{\rm \mu s}} \cdot \frac {68}{69}\hspace{0.15cm}\underline {\approx 768 \,\,{\rm kbit/s}}.$$

Hierbei ist berücksichtigt, dass ein jeder 69. Rahmen nur der Synchronisation dient.

(8)  Für das DMT–Spektrum gilt allgemein:

$$S((N - \mu ) \cdot f_0 ) = S^*(\mu \cdot f_0).$$

Mit N = 512 und $S(198 · f_0) = 1 + 3 · j$ gilt somit: $$S(314 \cdot f_0) \hspace{0.15cm}\underline {= 1 - 3 \cdot {\rm j}}.$$