Aufgaben:Aufgabe 1.1Z: Einfaches Pfadverlustmodell: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 7: | Zeile 7: | ||
:$$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},$$ | :$$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},$$ | ||
:$$V_{\rm 0} = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda} \hspace{0.05cm}.$$ | :$$V_{\rm 0} = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda} \hspace{0.05cm}.$$ | ||
| + | |||
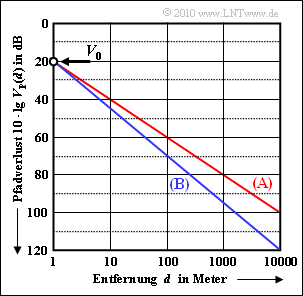
| + | Die Grafik zeigt den Pfadverlust <i>V</i><sub>P</sub>(<i>d</i>) in dB. Auch die Abszisse <i>d</i> ist logarithmisch dargestellt. In obiger Gleichung sind verwendet: | ||
Version vom 20. Oktober 2017, 18:31 Uhr
Bandbreitenorganisation bei DSL
Funkübertragung bei Sichtverbindung lässt sich durch das sog. Pfadverlustmodell beschreiben, das durch folgende Gleichungen gegeben ist:
- $$V_{\rm P}(d) = V_{\rm 0} + \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (d/d_0)\hspace{0.05cm},$$
- $$V_{\rm 0} = \gamma \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \frac{4 \cdot \pi \cdot d_0}{\lambda} \hspace{0.05cm}.$$
Die Grafik zeigt den Pfadverlust VP(d) in dB. Auch die Abszisse d ist logarithmisch dargestellt. In obiger Gleichung sind verwendet:
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.
