Aufgaben:Aufgabe 1.4: Rayleigh–WDF und Jakes–LDS

• Zurück zum Buch

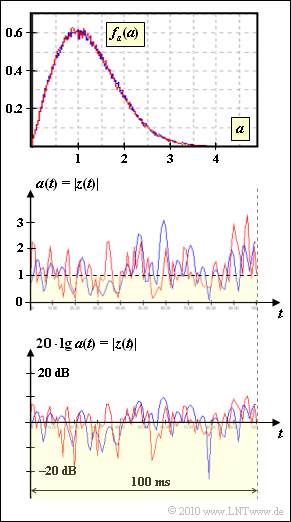
Wir betrachten zwei verschiedene Mobilfunkkanäle mit Rayleigh–Fading. In beiden Fällen lässt sich die WDF des Betrags $a(t) = |z(t)| ≥ 0$ in folgender Weise darstellen:

$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2}{2\sigma^2}] \hspace{0.05cm}.$$

Die Wahrscheinlichkeit, dass dieser Betrag kleiner oder gleich einem vorgegebenen Wert A ist, kann wie folgt berechnet werden:

$${\rm Pr}(|z(t)| \le A) = 1 - {\rm exp} [ -\frac{A^2}{2\sigma^2}] \hspace{0.05cm}.$$

Die beiden Kanäle, die entsprechend den Farben „Rot” und „Blau” in den Grafiken mit (R) bzw. (B) bezeichnet werden, unterscheiden sich durch die Geschwindigkeit υ und damit in der Form des Leistungsdichtespektrums Φ_z(f_D). In beiden Fällen ergibt sich aber ein Jakes–Spektrum. Für eine Dopplerfrequenz f_D, deren Betrag kleiner als ein Grenzwert f_D, max ist, lautet die Gleichung:

$${\it \Phi}_z(f_{\rm D}) = \frac{1}{\pi \hspace{-0.05cm}\cdot \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt{ 1 \hspace{-0.05cm}- \hspace{-0.05cm}(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.$$

Dopplerfrequenzen außerhalb dieses Intervalls von –f_D, max bis +f_D, max sind ausgeschlossen. Die entsprechende Beschreibungsgröße im Zeitbereich ist die Autokorrelationsfunktion (AKF):

$$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$

Hierbei bezeichnet J₀(.) die Besselfunktion erster Art und nullter Ordnung. Es gilt J₀(0) = 1. Vom Kanalmodell (R) ist die maximale Dopplerfrequenz bekannt: f_D, max = 200 Hz. Außerdem ist bekannt, dass sich die Geschwindigkeiten υ_R und υ_B um den Faktor 2 unterscheiden. Ob υ_R doppelt so groß ist als υ_B oder umgekehrt, sollen Sie anhand der obigen Grafiken entscheiden.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 1.3. Zur Überprüfung Ihrer Ergebnisse können Sie folgendes Interaktionsmodul benutzen:

1. WDF, VTF und Momente

Fragebogen

1

Ermitteln Sie den Rayleigh–Parameter σ für die Kanäle (R) und (B).

$\sigma_R \ = \ $ $\ \rm $

$\sigma_B \ = \ $ $\ \rm $

2

Geben Sie jeweils die Wahrscheinlichkeit an, dass 20 · lg a ≤ –10 dB ist, was gleichzeitig auch bedeutet, dass a ≤ 0.316 ist.

$(R):   Pr(a ≤ 0.316) \ = \ $ $\ \rm \%$

$(B):   Pr(a ≤ 0.316) \ = \ $ $\ \rm \%$

3

Welche Aussagen sind bezüglich den Fahrgeschwindigkeiten zutreffend?

	$\upsilon_B$ ist doppelt so groß als $\upsilon_R$.
	$\upsilon_B$ ist halb so groß als $\upsilon_R$.
	Mit $\upsilon = 0$ wäre $|z(t)|$ konstant.
	Mit $\upsilon = 0$ wäre $|z(t)|$ spektral gesehen weiß.
	Mit $\upsilon → ∞$ wäre $|z(t)|$ konstant.
	Mit $\upsilon → ∞$ wäre $|z(t)|$ weiß.

4

Welche der folgenden Aussagen sind richtig?

	Der LDS–Wert $\Phi_z(f_D = 0)$ ist bei beiden Kanälen gleich.
	Der AKF–Wert $\varphi_z(\Delta t = 0)$ ist bei beiden Kanälen gleich.
	Die Fläche unter $\Phi_z(f_D)$ ist bei beiden Kanälen gleich.
	Die Fläche unter $\varphi_z(\Delta t)$ ist bei beiden Kanälen gleich.

Musterlösung

Musterlösung

1. Aus der WDF erkennt man, dass das WDF–Maximum für beide Kanäle gleich 0.6 ist und für a = 1 auftritt. Die Rayleigh–WDF und ihre Ableitung lauten allgemein:

$$f_a(a) \hspace{-0.1cm} = \hspace{-0.1cm} \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2}{2\sigma^2}] \hspace{0.05cm},\\ \frac{{\rm d}f_a(a)}{{\rm d}a} \hspace{-0.1cm} = \hspace{-0.1cm} \frac{1}{\sigma^2} \cdot {\rm exp} [ -\frac{a}{2\sigma^2}]- \frac{a^2}{\sigma^4} \cdot {\rm exp} [ -\frac{a^2}{2\sigma^2}] \hspace{0.05cm}.$$

Durch Nullsetzen der Ableitung lässt sich zeigen, dass das WDF–Maximum bei a = σ auftritt. Da die Rayleigh–WDF für beide Kanäle gilt, folgt daraus:

$$\sigma_{\rm R} = \sigma_{\rm B} \hspace{0.15cm} \underline{ = 1} \hspace{0.05cm}.$$

2. Wegen der gleichen WDF ist auch die gesuchte Wahrscheinlichkeit für beide Kanäle gleich. Mit der angegebenen Gleichung erhält man hierfür:

$${\rm Pr}(a \le 0.316) = {\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a \le -10\,\,{\rm dB}) = 1 - {\rm exp} [ -\frac{0.316^2}{2\sigma^2}] = 1- 0.951 \hspace{0.15cm} \underline{ \approx 4.9 \%} \hspace{0.05cm}.$$

3. Richtig sind die Lösungsvorschläge 2, 3 und 6:

• Die kleinere Geschwindigkeit $\upsilon_B$ erkennt man daran, dass sich der Betrag $|z(t)|$ bei der blauen Kurve langsamer ändert.
• Bei stehendem Fahrzeug entartet das LDS zu $\Phi_z(f_D) = 2\sigma^2\cdot \delta(f_D)$, und es ist $|z(t)| = A = const.$, wobei die Konstante $A$ entsprechend der Rayleighverteilung ausgewürfelt wird.
• Bei extrem hoher Geschwindigkeit wird das Jakes–Spektrum über einen immer größeren Bereich flach und immer kleiner; es nähert sich dann dem LDS von weißem Rauschen an. Allerdings müsste dazu $\upsilon$ schon in der Größenordnung der Lichtgeschwindigkeit sein.

4. Richtig sind hier die beiden Aussagen 2 und 3. Durch den Rayleigh–Parameter $\sigma = 1$ liegt auch die „Leistung” $E[|z(t)|^2] = 2\sigma^2 = 2$ des Zufallsprozesses fest. Somit gilt sowohl für (R) als auch für (B):

$$\varphi_z ({\rm \Delta}t = 0) = 2 \hspace{0.05cm}, \hspace{0.2cm} \int_{-\infty}^{+\infty}{\it \Phi}_z(f_{\rm D}) \hspace{0.15cm}{\rm d}f_{\rm D} = 2 \hspace{0.05cm}.$$