Aufgaben:Aufgabe 3.1: Impulsantwort des Koaxialkabels: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 5: | Zeile 5: | ||
[[Datei:P_ID1370__Dig_A_3_1.png|right|frame]] | [[Datei:P_ID1370__Dig_A_3_1.png|right|frame]] | ||
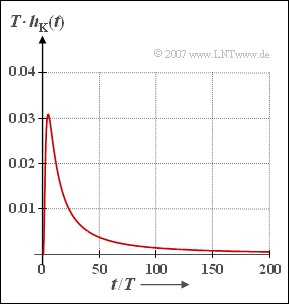
Der Frequenzgang eines Koaxialkabels der Länge $l$ ist durch folgende Formel darstellbar: | Der Frequenzgang eines Koaxialkabels der Länge $l$ ist durch folgende Formel darstellbar: | ||
| − | :$$H_{\rm K}(f) & = &{\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} | + | :$$H_{\rm K}(f) \& = \&{\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} |
\cdot \\ & \cdot & | \cdot \\ & \cdot & | ||
{\rm e}^{- (\alpha_1 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1) \hspace{0.05cm}\cdot f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot | {\rm e}^{- (\alpha_1 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1) \hspace{0.05cm}\cdot f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot | ||
Version vom 23. Oktober 2017, 11:24 Uhr
Der Frequenzgang eines Koaxialkabels der Länge $l$ ist durch folgende Formel darstellbar:
- $$H_{\rm K}(f) \& = \&{\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} \cdot \\ & \cdot & {\rm e}^{- (\alpha_1 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1) \hspace{0.05cm}\cdot f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot \\ & \cdot & {\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
(6)