Aufgaben:Aufgabe 3.2: Augendiagramm nach Gaußtiefpass

• Zurück zum Buch

Gegeben sei ein binäres bipolares redundanzfreies Basisbandsystem mit der Bitrate $R_B = 100\,{\rm Mbit/s}$ und folgenden Eigenschaften:

• Die Sendeimpulse seien rechteckförmig, die möglichen Amplitudenwerte sind $± 1\,{\rm V}$.
• Die AWGN–Rauschleistungsdichte (auf den Widerstand $1 \, \Omega$) ist $10^{\rm -9} \, {\rm V}^2/{\rm Hz}$.
• Als Empfangsfilter wird ein Gaußtiefpass mit der Grenzfrequenz $f_G = 50 \, {\rm MHz}$ verwendet. Der Frequenzgang lautet:

$$H_{\rm G}(f) = {\rm e}^{- \pi \hspace{0.05cm}\cdot \hspace{0.05cm}{f}^2/({2f_{\rm G}})^2} \hspace{0.05cm}.$$

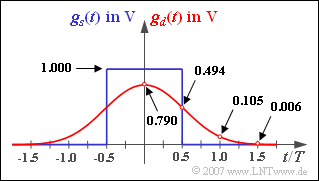
• Der Detektionsgrundimpuls $g_d(t) = g_s(t) * h_G(t)$ ist in der Grafik dargestellt (rote Kurve). Einige markante Impulswerte sind angegeben.
• Die Detektionsrauschleistung kann mit folgender Gleichung berechnet werden:

$$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f \hspace{0.05cm}.$$

Zur Bestimmung der Fehlerwahrscheinlichkeit kann man zum Beispiel das Augendiagramm heranziehen.

• Die mittlere Symbolfehlerwahrscheinlichkeit $p_S$ ergibt sich daraus nach einer Mittelung über alle möglichen Detektionsnutzabtastwerte.
• Als eine obere Schranke für $p_S$ dient die ungünstige Fehlerwahrscheinlichkeit.

$$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} \right) \hspace{0.3cm}{\rm mit}\hspace{0.3cm}\frac{\ddot{o}(T_{\rm D})}{ 2}= g_d(t=0) - |g_d(t=T)|- |g_d(t=-T)|-\hspace{0.15cm} ...$$

Hierbei bezeichnet $\ddot{o}(T_D)$ die vertikale Augenöffnung. Der Detektionszeitpunkt $T_D = 0$ sei optimal gewählt.

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 3.2. Verwenden Sie zur numerischen Auswertung der O–Funktion das folgende Interaktionsmodul: Komplementäre Gaußsche Fehlerfunktionen

Fragebogen

1

Wie groß ist die Symboldauer?

$T$ = ${\rm ns}$

2

Wie groß ist der Effektivwert des Detektionsrauschsignals?

$\sigma_d$ = ${\rm V}$

3

Wie lauten die Detektionsgrundimpulswerte $g_{\rm \nu} = g_d(\nu \cdot T)$, insbesondere

$g_0$ = ${\rm V}$

$g_1$ = ${\rm V}$

$g_2$ = ${\rm V}$

4

Berechnen Sie die Augenöffnung und die ungünstigste Fehlerwahrscheinlichkeit.

$\ddot{o}(T_D)$ = ${\rm V}$

$p_U$ = $\cdot 10^{\rm -3}$

5

Berechnen Sie die mittlere Fehlerwahrscheinlichkeit $p_S$ durch Mittelung über die möglichen Nutzabtastwerte.

$p_S$ = $\cdot 10^{\rm -4}$

6

Wie müsste die Sendeimpulsamplitude $s_0$ mindestens erhöt werden, damit die Bedingung $p_S ≤ 10^{\rm -10}$ erfüllt wird?

$s_0$ = ${\rm V}$

Musterlösung

Musterlösung

(1) Die Symboldauer ist der Kehrwert der Bitrate:

$$T = \frac{1}{10^8\,{\rm bit/s}} = 10^{-8}\,{\rm s}\hspace{0.15cm}\underline { = 10\,{\rm ns}} \hspace{0.05cm}.$$

(2) Die Integration entsprechend der angegebenen Gleichung führt auf:

$$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2}}= \frac{10^{-9}\,{\rm V/Hz} \cdot 5 \cdot 10^{7}\,{\rm Hz} }{\sqrt{2}}\approx 0.035\,{\rm V^2}$$

$$\Rightarrow \hspace{0.3cm}\sigma_d \hspace{0.15cm}\underline { = 0.188\,{\rm V}}\hspace{0.05cm}.$$

(3)

(4)

(5)

(6)