Aufgaben:Aufgabe 3.2Z: Optimale Grenzfrequenz bei Gauß-Tiefpass: Unterschied zwischen den Versionen

Version vom 26. Oktober 2017, 12:16 Uhr

Optimale Gauß–Grenzfrequenz

Wie in Aufgabe A3.2 wird ein binäres bipolares redundanzfreies Binärsystem mit gaußförmigen Empfangsfilter $H_G(f)$ betrachtet. Dessen Grenzfrequenz $f_G$ soll so bestimmt werden, dass das ungünstigste S/N–Verhältnis

$$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} \right)$$

maximal und damit die ungünsigste Fehlerwahrscheinlichkeit $p_U$ minimal wird. Die so optimierte Grenzfrequenz $f_{\rm G, \ opt}$ führt meist zur minimalen mittleren Symbolfehlerwahrscheinlichkeit $p_{\rm S, \ min}$.

In obiger Gleichung sind folgende Systemgrößen verwendet:

$\sigma_d^2$ ist die Detektionsrauschleistung. Bei gaußförmigen Empfangsfilter:

$$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2}}\hspace{0.05cm}.$$

$\ddot{o}(T_D)$ gibt die Augenöffnung an. Der Detektionszeitpunkt wird stets zu $T_D = 0$ angenommen.
Bei einem gaußförmigen Empfangsfilter kann die vertikale Augenöffnung $\ddot{o}(T_D)$ allein durch die Amplitude $s_0$ des Sendegrundimpulses (obere Begrenzung im Auge ohne Rauschen) sowie durch den Maximalwert $g_0$ des Detektionsgrundimpulses ausgedrückt werden. Die Impulsamplitude $g_0$ ist dabei wie folgt zu berechnen:

$$g_0 = g_d(t = 0) = s_0 \cdot \left [1- 2 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right]\hspace{0.05cm}.$$

Die Grafik zeigt die Augendiagramme der gesuchten Konfiguration mit optimaler Grenzfrequenz. Im oberen Diagramm sind die Rauschstörungen nicht berücksichtigt. Das untere Diagramm gilt dagegen mit AWGN–Rauschen für $10 \cdot \rm lg \ E_B/N_0 = 10 \ \rm dB$.

Hinweise:

Die Aufgabe bezieht sich auf das Kapitel Grundlagen der codierten Übertragung.
Verwenden Sie zur numerischen Auswertung der Q–Funktion das folgende Interaktionsmodul: Komplementäre Gaußsche Fehlerfunktionen

Fragebogen

	Die Berechnung der Augenöffnung erfolgt ohne Rauschen.
	Bei gaußförmigem Empfangsfilter gilt $\ddot{o}(T_D)/2 = s_0 \ – \ g_0$.
	Bei gaußförmigem Impulsformer gilt $\ddot{o}(T_D)/2 = 2 \cdot g_0 \ – \ s_0$

$f_{\rm G, \ min} \cdot T$ =

$f_G \cdot T = 0.6: \ 10 \cdot \rm lg \ \rho_U$ =

$\rm dB$

$f_G \cdot T = 0.8: \ 10 \cdot \rm lg \ \rho_U$ =

$\rm dB$

$f_G \cdot T = 1.0: \ 10 \cdot \rm lg \ \rho_U$ =

$\rm dB$

	Die Optimierung hinsichtlich $\rho_U$ (bzw. $\rho_U$) ergibt $f_{\rm G, \ opt} \cdot T \approx 0.8$.
	Dieses Optimierungsergebnis ist unabhängig von $E_B/N_0$.
	Die Optimierung hinsichtlich $p_S$ führt zum exakt gleichen Ergebnis.

$\ddot{o}(T_D)/s_0$ =

$\sigma_d/s_0$ =

$10 \cdot \rm lg \ \rho_U$ =

$\rm dB$

$p_U$ =

$\cdot 10^{\rm –5}$

Musterlösung

(1) Bei der Berechnung der vertikalen Augenöffnung darf der Rauschanteil nicht berücksichtigt werden. Dieser wird durch den Rauscheffektivwert $\sigma_d$ erfasst. Würde man die Augenöffnung aus dem unteren Augendiagramm auf der Angabenseite entnehmen, so würde die Rauschkomponente zweima erfasst.

Die obere Begrenzung der inneren Augenlinie ergibt sich für die Symbolfolge „ $\ ... \, \ –1 \ –1, +1, –1, \ – 1, \ ... \ $ ” . Die lange „$–1$”–Folge würde zum Wert $–s_0$ führen. Dagegen führt die „worst–case”–Folge zur Augenlinie $–s_0 + 2 \cdot g_d(t)$. Zum Detektionszeitpunkt $T_D = 0$ gilt somit mit der Entscheiderschwelle $E = 0$:

$${\ddot{o}(T_{\rm D})}/{ 2}= 2 \cdot g_0 - s_0 \hspace{0.05cm}.$$

Richtig sind somit der erste und der dritte Lösungsvorschlag.

(2) Für die halbe vertikale Augenöffnung gilt:

$${\ddot{o}(T_{\rm D})}/{ 2} \ = \ 2 \cdot g_0 - s_0 = 2 \cdot s_0 \cdot\left [ 1- 2 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right] - s_0 = $$

$$ \ = \ s_0 \cdot\left [ 1- 4 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right] \hspace{0.05cm}.$$

Ein geschlossenes Auge ergibt sich gemäß dem angegebenen Interaktionsmodul für

$${\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right) \ge 0.25 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sqrt{2\pi} \cdot f_{\rm G} \cdot T< 0.675$$

$$\hspace{0.3cm}\Rightarrow \hspace{0.3cm} f_{\rm G, min} \cdot T \approx \frac{0.675}{2.5}\hspace{0.15cm}\underline { \approx 0.27} \hspace{0.05cm}.$$

(3) Mit den Gleichungen auf der Angabenseite und den bisherigen Berechnungen ergibt sich

$$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2} = \frac{s_0^2 \cdot\left [ 1- 4 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right]^2}{ N_0 \cdot f_{\rm G} / \sqrt{2}}$$

Mit der Angabe $„E_B/N_0 = 10 \ \rm dB ”$ erhält man folgende Bestimmungsgleichung:

$$10 \cdot {\rm lg}\hspace{0.1cm} {E_{\rm B}}/{ N_0} = 10 \, {\rm dB}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {E_{\rm B}}/{ N_0} = {s_0^2 \cdot T}/{ N_0} = 10$$

$$\Rightarrow \hspace{0.3cm} \rho_{\rm U} = 10 \cdot \sqrt{2} \cdot \frac{ \left [ 1- 4 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right]^2}{ f_{\rm G} \cdot T}\hspace{0.05cm}.$$

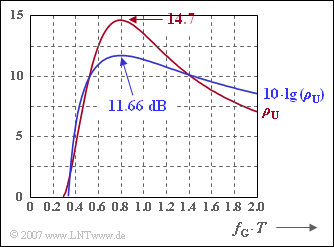
$\rho_U$ in Abhängigkeit der (normierten) Grenzfrequenz

Die Abbildung zeigt diesen Funktionsverlauf in Abhängigkeit der (normierten) Grenzfrequenz. Für die vorgegebenen Grenzfrequenzen gilt:

$f_G \cdot T = 0.6: \rho_{\rm U} \approx 12.7 \Rightarrow 10 \cdot \rm lg \ \rho_U \ \underline {\approx \ 11.04 \ \rm dB},$
$f_G \cdot T = 0.8: \rho_{\rm U} \approx 14.7 \Rightarrow 10 \cdot \rm lg \ \rho_U \ \underline {\approx \ 11.66 \ \rm dB},$
$f_G \cdot T = 1.0: \rho_{\rm U} \approx 13.5 \Rightarrow 10 \cdot \rm lg \ \rho_U \ \underline {\approx \ 11.30 \ \rm dB}.$

Aus obiger Grafik erkennt man auch die minimale Grenzfrequenz gemäß Teilaufgabe 2).

(4) Die Gültigkeit der ersten Aussage ergibt sich aus obiger Grafik. Da in der obigen Gleichung für $\rho_{\rm U}$ das Verhältnis $E_{\rm B}/N_0$ nur als Faktor auftritt, führt die Optimierung (Nullsetzen der Ableitung) unabhängig von $E_{\rm B}/N_0$ stets zum gleichen Ergebnis.

Die optimale Grenzfrequenz hinsichtlich $p_{\rm U}$ ist näherungsweise auch hinsichtlich $p_{\rm S}$ optimal, aber nicht exakt. Für sehr große Werte von $E_{\rm B}/N_0$ (kleines Rauschen) stimmt diese Näherung sehr gut und es gilt $p_{\rm S} \ \approx \ p_{\rm B}/4$. Dagegen ergibt sich bei großem Rauschen, beispielsweise $10 \cdot {\rm lg} \ E_{\rm B}/N_0 = 0 \ \rm dB$ eine kleinere optimale Grenzfrequenz, wenn die Optimierung auf $p_{\rm S}$ basiert:

$f_G \cdot T = 0.8: p_{\rm U} = 0.113, p_{\rm S} = 0.102,$
$f_G \cdot T = 0.6: p_{\rm U} = 0.129, p_{\rm S} = 0.094.$

Die Fehlerwahrscheinlichkeiten sind dann aber so groß, dass diese Ergebnisse nicht praxisrelevant sind. Richtig sind also die beiden ersten Lösungsvorschläge.

(5) Mit dem Ergebnis aus 2), $E_{\rm B}/N_0 = 10$ und $f_{\rm G} \cdot T = 0.8$ gilt:

$${\ddot{o}(T_{\rm D})}/{ s_0} = 2 \cdot \left [ 1- 4 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot 0.8 \right)\right] = 2 \cdot \left [ 1- 4 \cdot 0.022\right]\hspace{0.15cm}\underline { = 1.824} \hspace{0.05cm},$$

$${\sigma_d^2}/{ s_0^2} = \frac{N_0 \cdot f_{\rm G} }{\sqrt{2}\cdot s_0^2}= \frac{N_0 }{s_0^2 \cdot T} \cdot \frac{f_{\rm G} \cdot T}{\sqrt{2}} = 0.1 \cdot \frac{0.8}{\sqrt{2}} \approx 0.0566 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\sigma_d}/{ s_0}\hspace{0.15cm}\underline { \approx 0.238} \hspace{0.05cm},$$

$$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})]^2}{ 4 \cdot \sigma_d^2} = \frac{1.824^2}{ 4 \cdot 0.0566}\approx 14.7 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm} \rho_{\rm U}\hspace{0.15cm}\underline {\approx 11.66\, {\rm dB}} \hspace{0.05cm}.$$

$$p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} \right) = {\rm Q} \left( \sqrt{14.7} \right) \hspace{0.15cm}\underline { \approx 6.4 \cdot 10^{-5}}\hspace{0.05cm}.$$

@@ Zeile 123: / Zeile 123: @@
 * $f_G \cdot T = 0.8: p_{\rm U} = 0.113, p_{\rm S} = 0.102,$
 * $f_G \cdot T = 0.6: p_{\rm U} = 0.129, p_{\rm S} = 0.094.$
 Die Fehlerwahrscheinlichkeiten sind dann aber so groß, dass diese Ergebnisse nicht praxisrelevant sind. Richtig sind also die <u>beiden ersten Lösungsvorschläge</u>.