Aufgaben:Aufgabe 1.3Z: Nochmals Rayleigh–Fading?

• Zurück zum Buch

Zwei Kanäle, jeweils durch den komplexen Faktor z(t) gekennzeichnet

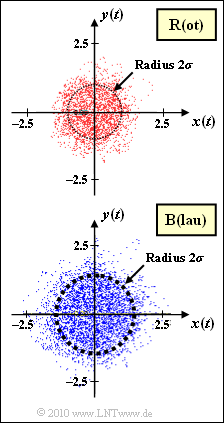
Dargestellt ist der multiplikative Faktor $z(t) = x(t) + j \cdot y(t)$ zweier Mobilfunkkanäle (beide ohne Mehrwegeausbreitung) in 2D–Darstellung. Als gesichert wird vorgegeben:

• Der Kanal R (die Bezeichnung ergibt sich aus der Farbe „Rot” der Punktwolke) ist rayleighverteilt mit $\sigma_{\rm R} = 0.5$.
• Für die Wahrscheinlichkeitsdichtefunktion (WDF) von Betrag $a(t) = |z(t)|$ bzw. Betragsquadrat $p(t) = |z(t)|^2$ gelten somit die folgenden Gleichungen (mit $\sigma = \sigma_{\rm R}$):

$$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm exp} [ -a^2/(2\sigma^2)] \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm},$$

$$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm exp} [ -p/(2\sigma^2)] \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} p \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} p < 0 \\ \end{array} .$$

• Vom Kanal B („Blau”) ist nur die Punktwolke gegeben. Es ist abzuschätzen, ob hier ebenfalls Rayleigh–Fading vorliegt, und wenn JA, wie groß bei diesem Kanal die Kenngröße $\sigma = \sigma_{\rm B}$ ist.
• In der Teilaufgabe 3) wird schließlich auch auf die WDF $f_{\it \phi}(\phi)$ der Phasenfunktion $\phi(t)$ Bezug genommen. Diese ist wie folgt definiert:

$$\phi(t) = \arctan \hspace{0.15cm} \frac{y(t)}{x(t)} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Wahrscheinlichkeitsdichte des Rayleigh–Fadings dieses Buches.
• Eine ähnliche Aufgabenstellung wird im Kapitel Weitere Verteilungen des Buches „Stochastische Signaltheorie” behandelt.

Fragebogen

1

Lässt sich auch der Kanal (B) durch „Rayleigh” modellieren?

	Ja.
	Nein.

2

Schätzen Sie den Rayleigh–Parameter von Kanal (B) ab. Zur Erinnerung: Bei Kanal (R) hat dieser Parameter den Wert $\sigma_{\rm R} = 0.5$.

$\sigma_{\rm B}$ =

3

Unterscheiden sich die Phasen–Wahrscheinlichkeitsdichtefunktionen $f_{\it \phi}(\phi)$ von Kanal (R) und (B), und wenn JA, wie?

	Ja.
	Nein.

4

Welchen Verlauf hat in beiden Fällen die WDF $f_a(a)$ mit $a(t) = |z(t)|$?

	Der Betrag $a(t)$ ist gaußverteilt.
	Der Betrag $a(t)$ ist rayleighverteilt.
	Der Betrag $a(t)$ ist positiv–exponentialverteilt.

5

Welchen Verlauf hat in beiden Fällen die WDF $f_p(p)$ mit $p(t) = |z(t)|^2$?

	Der Betrag $p(t)$ ist gaußverteilt.
	Der Betrag $p(t)$ ist rayleighverteilt.
	Der Betrag $p(t)$ ist positiv–exponentialverteilt.

6

Wie groß ist die Wahrscheinlichkeit, dass der Betrag $a(t) = |z(t)|$ größer ist als ein vorgegebener Wert $A$?

	Es gilt ${\rm Pr}(|z(t)|) > A) = {\rm ln}(A/\sigma)$.
	Es gilt ${\rm Pr}(|z(t)|) > A) = {\rm exp}[–A^2/2\sigma^2].
	Es gilt ${\rm Pr}(|z(t)|) > A) = {\rm exp}[–A/\sigma].

7

Input-Box Frage

$xyz$ = $ab$

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)