Aufgaben:Aufgabe 1.5: Nachbildung des Jakes–Spektrums: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
[[Datei:P_ID2124__Mob_A_1_5.png|right|frame]] | [[Datei:P_ID2124__Mob_A_1_5.png|right|frame]] | ||
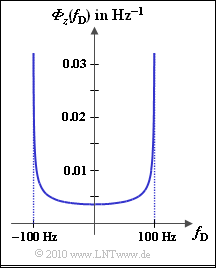
| − | Bei einem Mobilfunksystem macht sich der [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Ph.C3.A4nomenologische_Beschreibung_des_Dopplereffekts| | + | Bei einem Mobilfunksystem macht sich der [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Ph.C3.A4nomenologische_Beschreibung_des_Dopplereffekts|Dopplereffekt]] auch im Leistungsdichtespektrum der Dopplerfrequenz $f_{\rm D}$ bemerkbar. Es ergibt sich das sog. [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#AKF_und_LDS_bei_Rayleigh.E2.80.93Fading|Jakes–Spektrum]], das für die maximale Dopplerfrequenz $f_{\rm D, \ max} = 100 \ \rm Hz}$ in der Grafik dargestellt ist. ${\it \Phi}(f_{\rm D})$ hat nur Anteile innerhalb des Bereichs ,$\plusmn f_{\rm D, \ max}$ wobei gilt: |
:$${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } | :$${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Was im Frequenzbereich durch das Leistungsdichtespektrum ausgedrückt wird, beschreibt man im Zeitbereich durch die Autokorrelationsfunktion. Diese ergibt sich aus | + | Was im Frequenzbereich durch das Leistungsdichtespektrum ausgedrückt wird, beschreibt man im Zeitbereich durch die Autokorrelationsfunktion. Diese ergibt sich aus ${\it \Phi}_z(f_{\rm D}$ durch die [[Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation#Das_zweite_Fourierintegral|Fourierrücktransformation]]. |
| − | Mit der <i>Besselfunktion</i> erster Art und nullter Ordnung (J | + | Mit der <i>Besselfunktion</i> erster Art und nullter Ordnung (${\rm J}_0$) erhält man: |
:$$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$ | :$$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$ | ||
| − | Um den Dopplereffekt – und damit eine Relativbewegung zwischen Sender und Empfänger – bei einer Systemsimulation zu berücksichtigen, werden im [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Modellierung_von_nichtfrequenzselektivem_Fading| | + | Um den Dopplereffekt – und damit eine Relativbewegung zwischen Sender und Empfänger – bei einer Systemsimulation zu berücksichtigen, werden im [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Modellierung_von_nichtfrequenzselektivem_Fading|Rayleigh–Kanalmodell]] zwei digitale Filter eingefügt, jeweils mit dem Frequenzgang $H_{\rm DF}(f_D)$. Die Dimensionierung dieser Filter ist Inhalt dieser Aufgabe. |
| − | Wir beschränken uns hier auf den Zweig zur Generierung des Realteils | + | Wir beschränken uns hier auf den Zweig zur Generierung des Realteils $x(t)$. Für den Imaginärteil $y(t)$ ergeben sich genau gleiche Verhältnisse. |
| − | Am Eingang des im [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Frequenzselektives_Fading_vs._nichtfrequenzselektives_Fading| | + | Am Eingang des im [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Frequenzselektives_Fading_vs._nichtfrequenzselektives_Fading|Rayleigh–Kanalmodell]] linken digitalen Filters liegt weißes Gaußsches Rauschen $n(t)$ mit der Varianz $\sigma_^2 = 0.5$ an. Die Realteilkomponente ergibt sich dann gemäß der Faltung zu |
:$$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$ | :$$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$ | ||
| − | + | ''Hinweis:'' | |
| + | * Die Aufgabe gehört zum Kapitel [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses|Statistische Bindungen innerhalb des Rayleigh–Prozesses]] dieses Buches. | ||
| + | * Das digitale Filter wird im Kapitel [[Stochastische_Signaltheorie/Digitale_Filter|Digitale Filter]] des Buches „Stochastische Signaltheorie” ausführlich behandelt. | ||
Version vom 30. Oktober 2017, 12:05 Uhr
Bei einem Mobilfunksystem macht sich der Dopplereffekt auch im Leistungsdichtespektrum der Dopplerfrequenz $f_{\rm D}$ bemerkbar. Es ergibt sich das sog. Jakes–Spektrum, das für die maximale Dopplerfrequenz $f_{\rm D, \ max} = 100 \ \rm Hz}$ in der Grafik dargestellt ist. ${\it \Phi}(f_{\rm D})$ hat nur Anteile innerhalb des Bereichs ,$\plusmn f_{\rm D, \ max}$ wobei gilt:
- $${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.$$
Was im Frequenzbereich durch das Leistungsdichtespektrum ausgedrückt wird, beschreibt man im Zeitbereich durch die Autokorrelationsfunktion. Diese ergibt sich aus ${\it \Phi}_z(f_{\rm D}$ durch die Fourierrücktransformation. Mit der Besselfunktion erster Art und nullter Ordnung (${\rm J}_0$) erhält man:
- $$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$
Um den Dopplereffekt – und damit eine Relativbewegung zwischen Sender und Empfänger – bei einer Systemsimulation zu berücksichtigen, werden im Rayleigh–Kanalmodell zwei digitale Filter eingefügt, jeweils mit dem Frequenzgang $H_{\rm DF}(f_D)$. Die Dimensionierung dieser Filter ist Inhalt dieser Aufgabe. Wir beschränken uns hier auf den Zweig zur Generierung des Realteils $x(t)$. Für den Imaginärteil $y(t)$ ergeben sich genau gleiche Verhältnisse. Am Eingang des im Rayleigh–Kanalmodell linken digitalen Filters liegt weißes Gaußsches Rauschen $n(t)$ mit der Varianz $\sigma_^2 = 0.5$ an. Die Realteilkomponente ergibt sich dann gemäß der Faltung zu
- $$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$
Hinweis:
- Die Aufgabe gehört zum Kapitel Statistische Bindungen innerhalb des Rayleigh–Prozesses dieses Buches.
- Das digitale Filter wird im Kapitel Digitale Filter des Buches „Stochastische Signaltheorie” ausführlich behandelt.
Fragebogen
Musterlösung