Aufgaben:Aufgabe 2.1Z: Zur äquivalenten Bitrate: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Grundlagen der codierten Übertragung }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Mul…“) |
|||
| Zeile 5: | Zeile 5: | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1309__Dig_Z_2_1.png|right|frame|Quellen- und Codersignal]] |
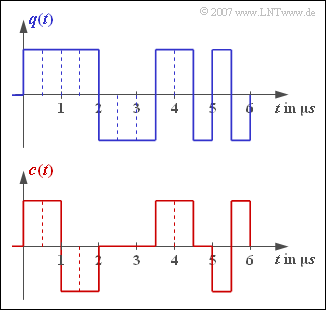
| + | Die obere Darstellung zeigt das Quellensignal $q(t)$ einer redundanzfreien Binärquelle mit Bitdauer $T_{q}$ und Bitrate $R_{q}$. Die beiden Signalparameter $T_{q}$ und $R_{q}$ können der Skizze entnommen werden. | ||
| + | Dieses Binärsignal wird symbolweise codiert und ergibt das unten gezeichnete Codersignal $c(t)$. Alle möglichen Codesymbole kommen in dem dargestellten Signalausschnitt der Dauer $6 / \rm \mu s$ vor. | ||
| + | Mit der Stufenzahl $M_{c}$ und der Symboldauer $T_{c}$ kann man die äquivalente Bitrate – oder den Informationsfluss – des Codersignals angeben: | ||
| + | :$$R_c = \frac{{\rm log_2} (M_c)}{T_c} \hspace{0.05cm}.$$ | ||
| + | Daraus erhält man die relative Redundanz des Codes, wenn man wie hier davon ausgeht, dass die Quelle selbst redundanzfrei ist: | ||
| + | :$$r_c = \frac{R_c - R_q}{R_c}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | ''Hinweis:'' | ||
| + | |||
| + | |||
| + | Die Aufgabe bezieht sich auf das [[Digitalsignalübertragung/Grundlagen_der_codierten_Übertragung|Grundlagen der codierten Übertragung]] dieses Buches. Bei dem hier betrachteten Übertragungscode handelt es sich um den Bipolarcode zweiter Ordnung, was jedoch für die Lösung dieser Aufgabe nicht von Bedeutung ist. | ||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 8. November 2017, 16:58 Uhr
Die obere Darstellung zeigt das Quellensignal $q(t)$ einer redundanzfreien Binärquelle mit Bitdauer $T_{q}$ und Bitrate $R_{q}$. Die beiden Signalparameter $T_{q}$ und $R_{q}$ können der Skizze entnommen werden.
Dieses Binärsignal wird symbolweise codiert und ergibt das unten gezeichnete Codersignal $c(t)$. Alle möglichen Codesymbole kommen in dem dargestellten Signalausschnitt der Dauer $6 / \rm \mu s$ vor. Mit der Stufenzahl $M_{c}$ und der Symboldauer $T_{c}$ kann man die äquivalente Bitrate – oder den Informationsfluss – des Codersignals angeben:
- $$R_c = \frac{{\rm log_2} (M_c)}{T_c} \hspace{0.05cm}.$$
Daraus erhält man die relative Redundanz des Codes, wenn man wie hier davon ausgeht, dass die Quelle selbst redundanzfrei ist:
- $$r_c = \frac{R_c - R_q}{R_c}\hspace{0.05cm}.$$
Hinweis:
Die Aufgabe bezieht sich auf das Grundlagen der codierten Übertragung dieses Buches. Bei dem hier betrachteten Übertragungscode handelt es sich um den Bipolarcode zweiter Ordnung, was jedoch für die Lösung dieser Aufgabe nicht von Bedeutung ist.
Fragebogen
Musterlösung