Aufgaben:Aufgabe 1.2Z: Nochmals Lognormal–Fading

• Zurück zum Buch

Pfadverlustmodell mit Lognormal-Fading

Wir gehen von ähnlichen Bedingungen wie in der Aufgabe 1.2 aus, fassen aber nun den rein entfernungsabhängigen Pfadverlust $V_0$ und den Mittelwert $m_{\rm S}$ des Lognormal–Fadings zusammen (der Index S steht für Shadowing):

$$V_{\rm 1} = V_{\rm 0} + m_{\rm S} \hspace{0.05cm}.$$

Der gesamte Pfadverlust ist dann durch die Gleichung

$$V_{\rm P} = V_{\rm 1} + V_{\rm 2}(t)$$

gegeben, wobei $V_2(t)$ eine Lognormal–Verteilung mit Mittelwert 0 beschreibt:

$$f_{V{\rm 2}}(V_{\rm 2}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ V_{\rm 2} ^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}.$$

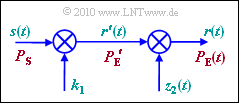
Das in der Grafik gezeigte Pfadverlustmodell ist für das hier beschriebene Szenario geeignet:

• Multipliziert man das Sendesignal $s(t)$ zunächst mit einem konstanten Faktor $k_1$ und weiter mit einer stochastischen Größe $z_2(t)$ mit der Wahrscheinlichkeitsdichte $f_{\rm z2}(z_2)$, so ergibt sich am Ausgang das Signal $r(t)$, dessen Leistung $P_{\rm E}(t)$ aufgrund des stochastischen Anteils natürlich ebenfalls zeitabhängig ist.
• Die WDF der lognormalverteilten Zufallsgröße $z_2$ lautet für $z_2 ≥ 0$:

$$f_{z{\rm 2}}(z_{\rm 2}) = \frac {{\rm exp } \left [ - {\rm ln}^2 (z_{\rm 2}) /({2 \cdot C^2 \cdot \sigma_{\rm S}^2}) \right ]}{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot z_2} \hspace{0.3cm}{\rm mit} \hspace{0.3cm} C = \frac{{\rm ln} \hspace{0.1cm}(10)}{20\,\,{\rm dB}}\hspace{0.05cm}.$$

• Für $z_2 ≤ 0$ ist diese WDF identisch Null.

Hinweise:

• Die Aufgabe gehört zum Kapitel Distanzabhängige Dämpfung und Abschattung.
• Verwenden Sie folgende Kenngrößen:

$$V_{\rm 1} = 60\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 6\,{\rm dB}\hspace{0.05cm}.$$

• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Die Wahrscheinlichkeit, dass eine mittelwertfreie Gaußsche Zufallsgröße $z$ größer ist als ihre Streuung $\sigma$, lautet:

$${\rm Pr}(z > \sigma) = {\rm Pr}(z < -\sigma) = {\rm Q}(1) \approx 0.158\hspace{0.05cm}.$$

• Außerdem gilt:   ${\rm Pr}(z > 2\sigma) = {\rm Pr}(z < -2\sigma) = {\rm Q}(2) \approx 0.023\hspace{0.05cm}.$
• Nochmals zur Verdeutlichung: $z_2$ ist die lineare Fading–Größe, während die Beschreibungsgröße $V_2$ auf dem Zehner–Logarithmus basiert. Es gelten folgende Umrechnungen:

$$z_2 = 10^{-V_{\rm 2}/20\,{\rm dB}}\hspace{0.05cm}, \hspace{0.2cm} V_{\rm 2} = -20\,{\rm dB} \cdot {\rm lg}\hspace{0.15cm}z_2\hspace{0.05cm}.$$

Fragebogen

1

Wie groß sollte die Konstante $k_1$ sein?

$k_1\ = \ $

2

Welcher Wertebereich gilt für die Zufallsgröße $z_2$?

	Es sind alle Werte zwischen $–∞$ und $+∞$ möglich.
	Die Zufallsgröße $z_2$ ist nicht negativ.
	Der kleinstmögliche Wert ist $z_2 = 0.5$.
	Der größtmögliche Wert ist $z_2 = 2$.

3

Berechnen Sie die WDF $f_{\rm z2}(z_2)$ für einige Abszissenwerte.

$f_{\rm z2}(z_2 = 0)\ = \ $

$f_{\rm z2}(z_2 = 1)\ = \ $

$f_{\rm z2}(z_2 = 2)\ = \ $

4

Berechnen Sie die folgenden Wahrscheinlichkeiten.

${\rm Pr}(z_2 > 1.0)\ = \ $

${\rm Pr}(z_2 > 0.5)\ = \ $

${\rm Pr}(z_2 > 4.0)\ = \ $

5

Welche Aussagen gelten für die mittlere Empfangsleistung ${\rm E}[P_{\rm E}(t)]$?
Hinweis: $P_{\rm E}'$ ist die Leistung nach der Multiplikation mit $k_1$ (siehe Grafik).

	Es gilt:   ${\rm E}[P_{\rm E}(t)] = P_{\rm E}'$.
	Es gilt:   ${\rm E}[P_{\rm E}(t)] < P_{\rm E}'$.
	Es gilt:   ${\rm E}[P_{\rm E}(t)] > P_{\rm E}'$.

Musterlösung

Musterlösung

(1)  Die Konstante $k_1$ erzeugt den zeitunabhängigen Pfadverlust $V_1 = 60 \ \rm dB$. Daraus folgt:

$$k_{\rm 1} = 10^{-V_{\rm 1}/(20\hspace{0.05cm} {\rm dB})} \hspace{0.15cm} \underline{= 0.001}\hspace{0.05cm}.$$

(2)  Richtig ist nur der zweite Lösungsvorschlag:

• Für die Gaußsche Zufallsvariable $V_2$ sind (theoretisch) alle Werte zwischen $–∞$ und $+∞$ möglich.
• Durch die Transformation $z_2 = 10^{{\it –V_2}\rm /20}$ ergeben sich für die lineare Zufallsgröße $z_2$ nur positive Werte und zwar zwischen 0 (falls $V_2$ positiv ist und bis ins Unendliche reicht) und $+∞$ (sehr große negative Werte von $V_2$).

(3)  Die Zufallsgröße $z_2$ kann nur positiv sein. Deshalb ist der WDF–Wert $f_{\rm z2}(z_2)\hspace{0.15cm} \underline{ = 0}$.

Der WDF–Wert für den Abszissenwert $z_2 = 1$ erhält man durch Einsetzen in die gegebene Gleichung:

$$f_{z{\rm 2}}(z_{\rm 2} = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {{\rm exp } \left [ - {\rm ln}^2 (z_2 = 1) /({2 \cdot C^2 \cdot \sigma_{\rm S}^2}) \right ]}{ \sqrt{2 \pi }\cdot C \cdot \sigma_{\rm S} \cdot (z_2 = 1)}=\frac {1}{ \sqrt{2 \pi } \cdot \sigma_{\rm S} } \cdot \frac {1}{ C } = \frac {1}{ \sqrt{2 \pi } \cdot 6\,\,{\rm dB} } \cdot \frac {20\,\,{\rm dB}}{ {\rm ln} \hspace{0.1cm}(10) } \hspace{0.15cm} \underline{\approx 0.578}\hspace{0.05cm}.$$

Der erste Anteil ist gleich dem WDF–Wert $f_{\it V2}(V_2 = 0)$ und $\rm C$ berücksichtigt den Betrag der Ableitung der nichtlinearen Kennlinie $z_2 = g(V_2)$ für $V_2 = 0 \ \rm dB$ bzw. $z_2 = 1$. Schließlich erhält man für $z_2 = 2$:

$$f_{z{\rm 2}}(z_{\rm 2} = 2) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac {f_{z{\rm 2}}(z_{\rm 2} = 1)}{ z_{\rm 2} = 2} \cdot {\rm exp } \left [ - \frac {{\rm ln}^2 (2)}{2 \cdot C^2 \cdot \sigma_{\rm S}^2} \right ]= \frac {0.578}{ 2} \cdot {\rm exp } \left [ - \frac {0.48}{0.952} \right ] \hspace{0.15cm} \underline{\approx 0.174}\hspace{0.05cm}. $$

(4)  Berücksichtigt man den Zusammenhang zwischen $z_2$ und $V_2$, so erhält man:

$${\rm Pr}(z_{\rm 2} > 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 0\,\,{\rm dB})\hspace{0.15cm} \underline{= 0.5} \hspace{0.05cm},$$

$${\rm Pr}(z_{\rm 2} > 0.5) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < 6\,\,{\rm dB}) = 1- {\rm Pr}(V_{\rm 2} > 6\,\,{\rm dB})= 1- {\rm Pr}(V_{\rm 2} > \sigma_{\rm S})= 1- {\rm Q}(1)\hspace{0.15cm} \underline{= 0.842} \hspace{0.05cm},$$

$${\rm Pr}(z_{\rm 2} > 4) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(V_{\rm 2} < -12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > +12\,\,{\rm dB}) = {\rm Pr}(V_{\rm 2} > 2 \sigma_{\rm S}) \hspace{0.05cm}.$$

Die Wahrscheinlichkeit, dass eine Gaußvariable größer ist als $2 \cdot \sigma$, ist aber gleich ${\rm Q}(2)$:

$${\rm Pr}(z_{\rm 2} > 4) = {\rm Q}(2)\hspace{0.15cm} \underline{= 0.023} \hspace{0.05cm}.$$

(5)  Die erste Aussage ist mit Sicherheit nicht zutreffend, da sich der Mittelwert $m_{\rm S}$ auf die logarithmierte Empfangsleistung (in $\rm dBm$) bezieht. Um zu klären, ob nun die zweite oder die dritte Lösungsalternative zutrifft, gehen wir von $P_{\rm S} = 1 \ \rm W$, $V_1 = 60 \ \rm dB$  ⇒  $P_{\rm E}' = 1 \ {\rm \mu W}$ und folgender $V_2$–WDF aus:

$$f_{V{\rm 2}}(V_{\rm 2}) = 0.5 \cdot \delta (V_{\rm 2}) + 0.25 \cdot \delta (V_{\rm 2}- 10\,\,{\rm dB}) + 0.25 \cdot \delta (V_{\rm 2}+ 10\,\,{\rm dB})\hspace{0.05cm}.$$

In der Hälfte der Zeit ist dann $P_{\rm E} = 1 \ \rm \mu W$, während in den beiden anderen Vierteln jeweils gilt:

$$V_{\rm 2}= +10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^7} = 0.1\,\,{\rm \mu W}\hspace{0.05cm},$$

$$V_{\rm 2}= -10\,\,{\rm dB}\text{:} \hspace{0.3cm} P_{\rm E}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1\,\,{\rm W}}{10^5} = 10\,\,{\rm \mu W}\hspace{0.05cm}.$$

Der Mittelwert ergibt somit:

$${\rm E}[P_{\rm E}(t)] = 0.5 \cdot 1\,{\rm \mu W}+ 0.25 \cdot 0.1\,{\rm \mu W}+0.25 \cdot 10\,{\rm \mu W}= 3.025\,{\rm \mu W} > P_{\rm E}\hspace{0.05cm}' = 1\,{\rm \mu W} \hspace{0.05cm}.$$

Diese einfache Rechnung mit diskreten Wahrscheinlichkeiten anstelle einer kontinuierlichen WDF deutet darauf hin, dass der dritte Lösungsvorschlag richtig sein wird.