Aufgaben:Aufgabe 1.4: Rayleigh–WDF und Jakes–LDS

• Zurück zum Buch

WDF und $|z(t)|$ bei Rayleigh-Fading mit Dopplereinfluss

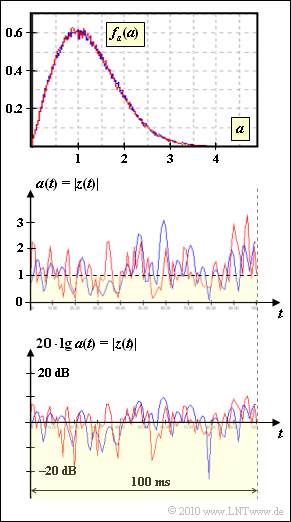
Wir betrachten zwei verschiedene Mobilfunkkanäle mit Rayleigh–Fading. In beiden Fällen lässt sich die WDF des Betrags $a(t) = |z(t)| ≥ 0$ in folgender Weise darstellen:

$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \hspace{0.05cm}.$$

Die Wahrscheinlichkeit, dass dieser Betrag kleiner oder gleich einem vorgegebenen Wert $A$ ist, kann wie folgt berechnet werden:

$${\rm Pr}(|z(t)| \le A) = 1 - {\rm e}^{ -{A^2}/(2\sigma^2)} \hspace{0.05cm}.$$

Die beiden Kanäle, die entsprechend den Farben „Rot” und „Blau” in den Grafiken mit R bzw. B bezeichnet werden, unterscheiden sich durch die Geschwindigkeit $v$ und damit in der Form des Leistungsdichtespektrums ${\it \Phi}_z(f_{\rm D})$.

• In beiden Fällen ergibt sich aber ein so genanntes Jakes–Spektrum.

• Für eine Dopplerfrequenz $f_{\rm D}$ mit $|f_{\rm D}| <f_{\rm D,\hspace{0.05cm}max}$ lautet die Gleichung:

$${\it \Phi}_z(f_{\rm D}) = \frac{1}{\pi \hspace{-0.05cm}\cdot \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt{ 1 \hspace{-0.05cm}- \hspace{-0.05cm}(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.$$

• Dopplerfrequenzen außerhalb dieses Intervalls von $–f_{\rm D,\hspace{0.05cm}max}$ bis $+f_{\rm D,\hspace{0.05cm}max}$ sind ausgeschlossen.

Die entsprechende Beschreibungsgröße im Zeitbereich ist die Autokorrelationsfunktion (AKF):

$$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$

• Hierbei bezeichnet ${\rm J_0}(.)$ die Besselfunktion erster Art und nullter Ordnung. Es gilt ${\rm J_0}(0) = 1$.
• Vom Kanalmodell R ist die maximale Dopplerfrequenz bekannt: $f_{\rm D,\hspace{0.05cm}max} = 200 \ \rm Hz$.
• Außerdem ist bekannt, dass sich die Geschwindigkeiten $v_{\rm R}$ und $v_{\rm B}$ um den Faktor 2 unterscheiden. Ob $v_{\rm R}$ doppelt so groß ist als $v_{\rm B}$ oder umgekehrt, sollen Sie anhand der obigen Grafiken entscheiden.

Hinweise:

• Die Aufgabe gehört zum Themengebiet von Statistische Bindungen innerhalb des Rayleigh–Prozesses.
• Zur Überprüfung Ihrer Ergebnisse können Sie das Interaktionsmodul WDF, VTF und Momente benutzen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Ermitteln Sie den Rayleigh–Parameter $\sigma$ für die Kanäle R und B.

$\sigma_{\rm R} \ = \ $ $\ \rm $

$\sigma_{\rm B} \ = \ $ $\ \rm $

2

Geben Sie jeweils die Wahrscheinlichkeit an, dass $20 \cdot {\rm lg} \ a ≤ –10 \ \rm dB$ ist, was gleichzeitig auch $a ≤ 0.316$ bedeutet.

${\rm (R)\text{:} \hspace{0.4cm}   Pr}(a ≤ 0.316) \ = \ $ $\ \rm \%$

${\rm (B)\text{:} \hspace{0.4cm}   Pr}(a ≤ 0.316) \ = \ $ $\ \rm \%$

3

Welche Aussagen sind bezüglich den Fahrgeschwindigkeiten zutreffend?

	$v_{\rm B}$ ist doppelt so groß als $v_{\rm R}$.
	$v_{\rm B}$ ist halb so groß als $v_{\rm R}$.
	Mit $v = 0$ wäre $|z(t)|$ konstant.
	Mit $v = 0$ wäre $|z(t)|$ spektral gesehen weiß.
	Mit $v → ∞$ wäre $|z(t)|$ konstant.
	Mit $v → ∞$ wäre $|z(t)|$ weiß.

4

Welche der folgenden Aussagen sind richtig?

	Der LDS–Wert ${\it \Phi_z}(f_{\rm D} = 0)$ ist bei beiden Kanälen gleich.
	Der AKF–Wert $\varphi_z(\Delta t = 0)$ ist bei beiden Kanälen gleich.
	Die Fläche unter ${\it \Phi_z}(f_{\rm D})$ ist bei beiden Kanälen gleich.
	Die Fläche unter $\varphi_z(\Delta t)$ ist bei beiden Kanälen gleich.

Musterlösung

Musterlösung

(1)  Aus der WDF erkennt man, dass das WDF–Maximum für beide Kanäle gleich $0.6$ ist und für $a = 1$ auftritt. Die Rayleigh–WDF und ihre Ableitung lauten allgemein:

$$f_a(a) \hspace{-0.1cm} = \hspace{-0.1cm} \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2}{2\sigma^2}] \hspace{0.05cm},$$

$$\frac{{\rm d}f_a(a)}{{\rm d}a} \hspace{-0.1cm} = \hspace{-0.1cm} \frac{1}{\sigma^2} \cdot {\rm exp} [ -\frac{a}{2\sigma^2}]- \frac{a^2}{\sigma^4} \cdot {\rm exp} [ -\frac{a^2}{2\sigma^2}] \hspace{0.05cm}.$$

Durch Nullsetzen der Ableitung lässt sich zeigen, dass das WDF–Maximum bei $a = \sigma$ auftritt. Da die Rayleigh–WDF für beide Kanäle gilt, folgt daraus:

$$\sigma_{\rm R} = \sigma_{\rm B} \hspace{0.15cm} \underline{ = 1} \hspace{0.05cm}.$$

(2)  Wegen der gleichen WDF ist auch die gesuchte Wahrscheinlichkeit für beide Kanäle gleich. Mit der angegebenen Gleichung erhält man hierfür:

$${\rm Pr}(a \le 0.316) = {\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a \le -10\,\,{\rm dB}) = 1 - {\rm exp} [ -\frac{0.316^2}{2\sigma^2}] = 1- 0.951 \hspace{0.15cm} \underline{ \approx 4.9 \%} \hspace{0.05cm}.$$

(3)  Richtig sind die Lösungsvorschläge 2, 3 und 6:

• Die kleinere Geschwindigkeit $\upsilon_{\rm B}$ erkennt man daran, dass sich der Betrag $|z(t)|$ bei der blauen Kurve langsamer ändert.
• Bei stehendem Fahrzeug entartet das LDS zu ${\it \Phi_z}(f_{\rm D}) = 2\sigma^2\cdot \delta(f_{\rm D})$, und es ist $|z(t)| = A = \rm const.$, wobei die Konstante $A$ entsprechend der Rayleighverteilung ausgewürfelt wird.
• Bei extrem hoher Geschwindigkeit wird das Jakes–Spektrum über einen immer größeren Bereich flach und immer kleiner; es nähert sich dann dem LDS von weißem Rauschen an. Allerdings müsste dazu $\upsilon$ schon in der Größenordnung der Lichtgeschwindigkeit sein.

(4)  Richtig sind hier die beiden Aussagen 2 und 3. Durch den Rayleigh–Parameter $\sigma = 1$ liegt auch die „Leistung” ${\rm E}[|z(t)|^2] = 2\sigma^2 = 2$ des Zufallsprozesses fest. Somit gilt sowohl für (R) als auch für (B):

$$\varphi_z ({\rm \Delta}t = 0) = 2 \hspace{0.05cm}, \hspace{0.2cm} \int_{-\infty}^{+\infty}{\it \Phi}_z(f_{\rm D}) \hspace{0.15cm}{\rm d}f_{\rm D} = 2 \hspace{0.05cm}.$$