Aufgaben:Aufgabe 1.5: Nachbildung des Jakes–Spektrums: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Mobile Kommunikation/Statistische Bindungen innerhalb des Rayleigh-Prozesses}} | {{quiz-Header|Buchseite=Mobile Kommunikation/Statistische Bindungen innerhalb des Rayleigh-Prozesses}} | ||
| − | [[Datei:P_ID2124__Mob_A_1_5.png|right|frame]] | + | [[Datei:P_ID2124__Mob_A_1_5.png|right|frame|Betrachtetes Jakes–Spektrum]] |
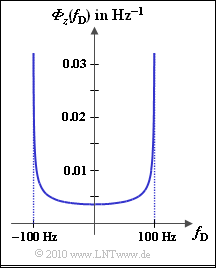
| − | Bei einem Mobilfunksystem macht sich der [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Ph.C3.A4nomenologische_Beschreibung_des_Dopplereffekts|Dopplereffekt]] auch im Leistungsdichtespektrum der Dopplerfrequenz $f_{\rm D}$ bemerkbar. Es ergibt sich das | + | Bei einem Mobilfunksystem macht sich der [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Ph.C3.A4nomenologische_Beschreibung_des_Dopplereffekts|Dopplereffekt]] auch im Leistungsdichtespektrum der Dopplerfrequenz $f_{\rm D}$ bemerkbar. Es ergibt sich das so genannte [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#AKF_und_LDS_bei_Rayleigh.E2.80.93Fading|Jakes–Spektrum]], das für die maximale Dopplerfrequenz $f_{\rm D, \ max} = 100 \ \rm Hz$ in der Grafik dargestellt ist. ${\it \Phi}_z(f_{\rm D})$ hat nur Anteile innerhalb des Bereichs $± f_{\rm D, \ max}$ wobei gilt: |
:$${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } | :$${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Was im Frequenzbereich durch das Leistungsdichtespektrum ausgedrückt wird, beschreibt man im Zeitbereich durch die Autokorrelationsfunktion. Diese ergibt sich aus ${\it \Phi}_z(f_{\rm D}$ durch die [[Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation#Das_zweite_Fourierintegral|Fourierrücktransformation]]. | Was im Frequenzbereich durch das Leistungsdichtespektrum ausgedrückt wird, beschreibt man im Zeitbereich durch die Autokorrelationsfunktion. Diese ergibt sich aus ${\it \Phi}_z(f_{\rm D}$ durch die [[Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation#Das_zweite_Fourierintegral|Fourierrücktransformation]]. | ||
| + | |||
Mit der <i>Besselfunktion</i> erster Art und nullter Ordnung (${\rm J}_0$) erhält man: | Mit der <i>Besselfunktion</i> erster Art und nullter Ordnung (${\rm J}_0$) erhält man: | ||
:$$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$ | :$$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$ | ||
| − | Um den Dopplereffekt – und damit eine Relativbewegung zwischen Sender und Empfänger – bei einer Systemsimulation zu berücksichtigen, werden im [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Modellierung_von_nichtfrequenzselektivem_Fading|Rayleigh–Kanalmodell]] zwei digitale Filter eingefügt, jeweils mit dem Frequenzgang $H_{\rm DF}(f_D)$. Die Dimensionierung dieser Filter ist Inhalt dieser Aufgabe. | + | Um den Dopplereffekt – und damit eine Relativbewegung zwischen Sender und Empfänger – bei einer Systemsimulation zu berücksichtigen, werden im [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Modellierung_von_nichtfrequenzselektivem_Fading|Rayleigh–Kanalmodell]] zwei digitale Filter eingefügt, jeweils mit dem Frequenzgang $H_{\rm DF}(f_D)$. |
| − | Wir beschränken uns hier auf den Zweig zur Generierung des Realteils $x(t)$. Für den Imaginärteil $y(t)$ ergeben sich genau gleiche Verhältnisse. | + | |
| − | Am Eingang des im [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Frequenzselektives_Fading_vs._nichtfrequenzselektives_Fading|Rayleigh–Kanalmodell]] linken digitalen Filters liegt weißes Gaußsches Rauschen $n(t)$ mit der Varianz $\sigma^2 = 0.5$ an. Die Realteilkomponente ergibt sich dann gemäß der Faltung zu | + | Die Dimensionierung dieser Filter ist Inhalt dieser Aufgabe. |
| + | *Wir beschränken uns hier auf den Zweig zur Generierung des Realteils $x(t)$. Für den Imaginärteil $y(t)$ ergeben sich genau gleiche Verhältnisse. | ||
| + | *Am Eingang des im [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Frequenzselektives_Fading_vs._nichtfrequenzselektives_Fading|Rayleigh–Kanalmodell]] linken digitalen Filters liegt weißes Gaußsches Rauschen $n(t)$ mit der Varianz $\sigma^2 = 0.5$ an. Die Realteilkomponente ergibt sich dann gemäß der Faltung zu | ||
:$$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$ | :$$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$ | ||
| − | '' | + | |
| − | * Die Aufgabe gehört zum | + | ''Hinweise:'' |
| + | * Die Aufgabe gehört zum Themengebiet von [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses|Statistische Bindungen innerhalb des Rayleigh–Prozesses]]. | ||
* Das digitale Filter wird im Kapitel [[Stochastische_Signaltheorie/Digitale_Filter|Digitale Filter]] des Buches „Stochastische Signaltheorie” ausführlich behandelt. | * Das digitale Filter wird im Kapitel [[Stochastische_Signaltheorie/Digitale_Filter|Digitale Filter]] des Buches „Stochastische Signaltheorie” ausführlich behandelt. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
Version vom 13. November 2017, 08:03 Uhr
Bei einem Mobilfunksystem macht sich der Dopplereffekt auch im Leistungsdichtespektrum der Dopplerfrequenz $f_{\rm D}$ bemerkbar. Es ergibt sich das so genannte Jakes–Spektrum, das für die maximale Dopplerfrequenz $f_{\rm D, \ max} = 100 \ \rm Hz$ in der Grafik dargestellt ist. ${\it \Phi}_z(f_{\rm D})$ hat nur Anteile innerhalb des Bereichs $± f_{\rm D, \ max}$ wobei gilt:
- $${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.$$
Was im Frequenzbereich durch das Leistungsdichtespektrum ausgedrückt wird, beschreibt man im Zeitbereich durch die Autokorrelationsfunktion. Diese ergibt sich aus ${\it \Phi}_z(f_{\rm D}$ durch die Fourierrücktransformation.
Mit der Besselfunktion erster Art und nullter Ordnung (${\rm J}_0$) erhält man:
- $$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$
Um den Dopplereffekt – und damit eine Relativbewegung zwischen Sender und Empfänger – bei einer Systemsimulation zu berücksichtigen, werden im Rayleigh–Kanalmodell zwei digitale Filter eingefügt, jeweils mit dem Frequenzgang $H_{\rm DF}(f_D)$.
Die Dimensionierung dieser Filter ist Inhalt dieser Aufgabe.
- Wir beschränken uns hier auf den Zweig zur Generierung des Realteils $x(t)$. Für den Imaginärteil $y(t)$ ergeben sich genau gleiche Verhältnisse.
- Am Eingang des im Rayleigh–Kanalmodell linken digitalen Filters liegt weißes Gaußsches Rauschen $n(t)$ mit der Varianz $\sigma^2 = 0.5$ an. Die Realteilkomponente ergibt sich dann gemäß der Faltung zu
- $$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Themengebiet von Statistische Bindungen innerhalb des Rayleigh–Prozesses.
- Das digitale Filter wird im Kapitel Digitale Filter des Buches „Stochastische Signaltheorie” ausführlich behandelt.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $${\it \Phi}_x(f_{\rm D} = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\it \Phi}_y(f_{\rm D} = 0) = \frac{{\it \Phi}_z(f_{\rm D} = 0)}{2}=$$
- $$ \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{\sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max}} = \frac{0.5}{\pi \cdot 100\,\,{\rm Hz}} \hspace{0.15cm} \underline{ = 1.59 \cdot 10^{-3}\,\,{\rm Hz^{-1}}} \hspace{0.05cm}.$$
(2) Richtig ist der Lösungsvorschlag 2. Das Eingangssignal $n(t)$ besitzt ein weißes (konstantes) LDS ${\it \Phi}_n(f_{\rm D})$. Für das LDS am Ausgang gilt dann:
- $${\it \Phi}_x(f_{\rm D}) = {\it \Phi}_n(f_{\rm D}) \cdot | H_{\rm DF}(f_{\rm D}|^2 \hspace{0.05cm}.$$
(3) Richtig ist der letzte Lösungsvorschlag. Nur wenn diese Bedingung erfüllt ist, hat das Signal $x(t)$ die gleiche Varianz $\sigma^2$ wie das Rauschsignal $n(t)$.
(4) Richtig ist NEIN. Die beiden Bedingungen nach den Teilaufgaben (2) und (3) beziehen sich nur auf die Betragsfunktion. Für die Phase des digitalen Filters gibt es keine Vorschrift. Diese ist frei wählbar. Meist wählt man diese so, dass sich ein minimalphasiges Netzwerk ergibt. In diesem Fall hat dann die Impulsantwort $h_{\rm DF}(t)$ die geringst mögliche Ausdehnung.
Die Grafik zeigt das Ergebnis einer solchen Approximation. Die roten Kurven wurden simulativ über 100.000 Abtastwerte ermittelt. Man erkennt:
- Das Jakes–Leistungsdichtespektrum (linke Grafik) lässt sich aufgrund des senkrechten Abfalls bei $± f_{\rm D, \ max}$ nur sehr ungenau nachbilden.
- Für den Zeitbereich bedeutet dies, dass die AKF sehr viel schneller abfällt, als es die Theorie besagt. Für kleine $\Delta t$–Werte ist die Approximation aber sehr gut (rechte Grafik).