Signaldarstellung/Fouriertransformation und -rücktransformation

1. Signaldarstellung
2. Aperiodische Signale - Implulse
3. Fouriertransformation und -rücktransformation

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Eigenschaften aperiodischer Signale

Im letzten Kapitel haben wir periodische Signale betrachtet. Das wesentliche Charakteristikum dieser Signale ist, dass für sie eine Periodendauer $T_0$ angegeben werden kann. Ist eine solche Periodendauer nicht angebbar oder – was in der Praxis das gleiche ist – hat $T_0$ einen unendlich großen Wert, so spricht man von einem aperiodischen Signal. Für das gesamte Kapitel 3 sollen folgende Voraussetzungen gelten:

• Die betrachteten Signale $x(t)$ sind aperiodisch und energiebegrenzt, das heißt, sie besitzen nur eine endliche Energie $E_x$ und eine vernachlässigbar kleine (mittlere) Leistung $P_x$.
• Im Allgemeinen konzentriert sich die Energie dieser Signale auf einen relativ kurzen Zeitbereich, so dass man auch von impulsförmigen Signalen spricht.

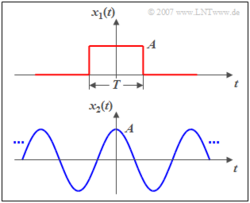
Das folgende Bild zeigt einen Rechteckimpuls $x_1(t)$ mit Amplitude $A$ und Dauer $T$ als Beispiel eines aperiodischen und zeitlich begrenzten Signals. Dieser besitzt eine endliche Signalenergie ($E_1=A^2 \cdot T$) und die Leistung $P_1$ = 0.

Ein leistungsbegrenztes Signal, z. B. das unten dargestellte Cosinussignal $x_1(t)$, besitzt dagegen

• stets eine endliche Leistung ($P_2=A^2/2$), und
• eine unendlich große Signalenergie ($E_2 \to \infty$).

Genauere Betrachtung der Fourierkoeffizienten

Wir gehen von einem periodischen Signal $x_P(t)$ mit der Periodendauer $T_0$ aus, das entprechend den Ausführungen im Kapitel 2.4 als (komplexe) Fourierreihe dargestellt werden kann:

$$x_{\rm P}(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j 2 \pi \hspace{-0.05cm}{\it n} \it t / T_{\rm 0}}.$$

Die Fourierkoeffizienten sind im Allgemeinen komplex, und es gilt $D_{-n}=D_n^\ast$:

$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} \it t / T_{\rm 0}}\, {\rm d}t.$$

Wie bereits im Kapitel 2.4 gezeigt wurde, ist die dazugehörige Spektralfunktion $X_p(f)$ ein so genanntes Linienspektrum mit Spektrallinien im Abstand $f_0=1/T_0$:

$$X_{\rm P}(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$

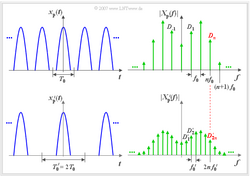
Das Bild zeigt links das periodische Zeitsignal und rechts das zugehörige Betragsspektrum.

Anzumerken ist, dass es sich hierbei lediglich um eine schematische Skizze handelt. Ist $x_P(t)$ eine reelle und gerade Funktion, so ist $X_P(f)$ ebenfalls reell und gerade. Die Gleichung $X_P(f) = |X_P(f)|$ gilt allerdings nur dann, wenn alle Spektrallinien zudem auch positiv sind.

Im unteren Bild ist ein weiteres periodisches Signal $x_P'(t)$ mit doppelter Periodendauer $T_0' = 2 \cdot T_0$ dargestellt. Bezüglich dieses Signals gilt:

$${x_{\rm P}}'(t)=\sum^{+\infty}_{n=-\infty}{\it D_n}'\cdot {\rm e}^{{\rm j} 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}'} \hspace{0.3cm}{\rm mit}\hspace{0.3cm}{\it D_n}'=\frac{1}{{T_0}'}\cdot \int^{{+T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}'}\, {\rm d}\it t.$$

Im Bereich von $-T_0/2$ bis $+t_0/2$ sind die beiden Signale identisch.

Betrachten wir auch hier die Spektralfunktion $X_P'(f)$: Aufgrund der doppelten Periodendauer ($T_0' = 2 \cdot T_0$) liegen nun die Spektrallinien enger beisammen ($f_0' = f_0/2$). Die beiden Koeffizienten $D_n$ und $D_{2n}'$ – im Bild rot hervorgehoben – gehören zur gleichen physikalischen Frequenz $f = n \cdot f_0 = 2n \cdot f_0'$.

Durch Analyse der Koeffizienten

$${D_{2n}}'=\frac{1}{{T_0}'}\cdot \int^{+{T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} \it t / {T_{\rm 0}}'}\, {\rm d}t$$

erkennen wir:

• Zwischen $T_0/2$ und $T_0'/2$ ist $x_P'(t)$ identisch 0, ebenso im dazu symmetrischen Intervall bei negativen Zeiten. Deshalb können die Integrationsgrenzen auf $\pm T_0/2$ eingeschränkt werden.
• Innerhalb der neuen Integrationsgrenzen kann $x_P'(t)$ durch $x_P(t)$ ersetzt werden.

Setzen wir nun in obiger Gleichung noch $T_0' = 2T_0$, so erhalten wir:

$${D_{2n}}'=\frac{1}{2T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} t / T_{\rm 0}}\, {\rm d}t = \frac{D_n}{2} .$$

Fassen wir dieses Ergebnis kurz zusammen:

• Die Spektrallinie des Signals $x_P'(t)$ bei der Frequenz $f = n \cdot f_0'$ wird mit $D_{2n}'$ bezeichnet (untere Grafik). Diese Linie ist genau halb so groß wie die Spektrallinie $D_n$ des Signals $x_P(t)$ bei der gleichen physikalischen Frequenz $f$ (obere Grafik).
• Die Spektralfunktion $X_P'(f)$ weist gegenüber $X_P(f)$ zusätzliche Spektrallinien bei $(n + 1/2) \cdot f_0$ auf. Diese führen dazu, dass im Zeitbereich jeder zweite Impuls von $x_P(t)$ um $n \cdot T_0$ gelegen ($n$ ungeradzahlig) ausgelöscht wird.

Vom periodischen zum aperiodischen Signal

Greifen wir nun die Überlegungen der vorherigen Seite auf und wählen die Periodendauer $T_0'$ von $x_P'(t)$ allgemein um einen ganzzahligen Faktor $k$ größer als die Periodendauer $T_0$ von $x_P(t)$. Dann können die bisherigen Aussagen verallgemeinert werden:

• Der Linienabstand ist bei $X_P'(f)$ um den Faktor $k$ geringer als beim Spektrum $X_P(f)$.
• Um diesen Sachverhalt hervorzuheben, bezeichnen wir die Frequenz-Laufvariable der Funktion $X_P'(f)$ mit $v$ anstelle von $n$. Es gilt: $v=k \cdot n$.
• Für die Spektrallinie des Signals $X_P'(f)$ bei der Frequenz $f=n \cdot f_0 = v \cdot f_0'$ gilt:

$${D_\nu}' = \frac{1}{k} \cdot D_n, \hspace{0.5cm} {\rm wobei} \hspace{0.5cm} \nu = k \cdot n .$$

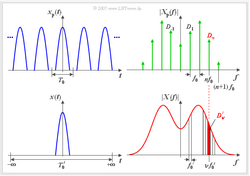
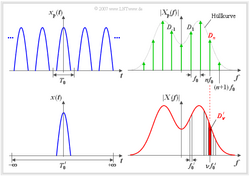
Wählt man nun – wie im Bild schematisch dargestellt – den Faktor $k$ und damit die Periodendauer $T_0'$ immer größer und lässt sie schließlich nach unendlich gehen, so

• geht das periodische Signal $x_P(t)$ in das aperiodische Signal $x(t)$ über,
• kann man das Linienspektrum $X_P(f)$ durch das kontinuierliche Spektrum $X(f)$ ersetzen.

Das erste Fourierintegral

Bezüglich den Spektralfunktion $X_P(f)$ und $X(f)$ lassen sich somit folgende Aussagen machen:

• Die einzelnen Spektrallinien liegen nun beliebig eng beieinander ($f_0'=1/T_0' \to 0$).
• In der Spektralfunktion $X(f)$ treten nun innerhalb bestimmter Intervalle alle möglichen (nicht nur diskrete) Frequenzen auf; $X(f)$ stellt also kein Linienspektrum mehr dar.
• Der Beitrag einer jeden einzelnen Frequenz $f$ zum Signal ist nur verschwindend gering ($k \to \infty, D_v' \to 0$). Aufgrund der unendlich vielen Frequenzen ergibt sich jedoch insgesamt ein endliches Resultat.
• Anstatt die Fourierkoeffizienten $D_v'$ zu berechnen, wird nun stattdessen eine spektrale Dichte $X(f)$ ermittelt. Bei der Frequenz $f=v \cdot f_0'$ gilt dann:

$$X(f = {\rm \nu} {f_{\rm 0}}') = \lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm} 0} ({{D_{\rm \nu}}'}/{{f_{\rm 0}}'}) = \lim_{{T_{\rm 0}}' \to \infty} ({D_{\rm \nu}}' \cdot {T_{\rm 0}}')$$ .

• Die Spektralfunktion (Dichte) $X(f)$ des aperiodischen Signals $x(t)$ ist im Spektrum $X_P(f)$ des vergleichbaren periodischen Signals $x_P(t)$ als Einhüllende erkennbar (siehe Grafiken).
• In der unteren Grafik entspricht $D_v'$ der rot hinterlegten Fläche des Frequenzintervalls um $v \cdot f_0'$ mit der Breite $f_0'$.

Verwendet man die auf der letzten Seite angegebenen Gleichungen, so erhält man:

$$X(f = {\rm \nu} \cdot {f_{\rm 0}}') = \lim_{{T_{\rm 0}'} \to \infty} \int ^{{T_{\rm 0}}'/2} _{-{T_{\rm 0}}'/2} x_{\rm P}(t) \, \cdot \, { \rm e}^{-\rm j 2\pi\nu \it {f_{\rm 0}}' t} \,{\rm d}t.$$

Durch den gemeinsamen Grenzübergang ($T_0' \to \infty, f_0' \to 0$) wird nun

• aus dem periodischen Signal $x_P(t)$ das aperiodische Signal $x(t)$, und
• aus der diskreten Frequenz $v \cdot f_0'$ die kontinuierliche Frequenzvariable $f$.

Damit erhält man eine fundamentale Definition, welche die Berechnung der Spektralfunktion einer aperiodischen Zeitfunktion ermöglicht. Der Name dieser Spektraltransformation geht auf den französischen Physiker Jean-Baptiste-Joseph Fourier zurück.

Die Spektralfunktion (oder kurz: das Spektrum) eines aperiodischen und gleichzeitig energiebegrenzten Signals $x(t)$ ist wie folgt zu berechnen:

$$X(f)= \hspace{0.05cm}\int \limits_{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t$$

⇒ Erstes Fourierintegral.

Das nachfolgende Lernvideo soll Ihnen die Aussagen der letzten Seiten nochmals verdeutlichen: Unterschiede und Gemeinsamkeiten von kontinuierlichen und diskreten Spektren (Dauer Teil 1: 6:20 – Teil 2: 5:15)

Beispiel zum ersten Fourierintegral

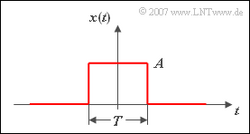
Gegeben ist der skizzierte Zeitverlauf $x(t)$. Gesucht ist das zugehörige Spektrum $X(f)$.

Wir wenden dazu das erste Fourierintegral an. Aus obiger Darstellung ist zu erkennen, dass das Signal $x(t)$ für $|t| > T/2$ gleich 0 ist. Das bedeutet, dass das Integrationsintervall auf den Bereich $\pm T/2$ begrenzt werden kann. Damit erhält man den Ansatz:

$$ \begin{align*} X(f) & = A \int_{-T/2}^{+T/2} {\rm e}^{-{\rm j2\pi} ft}\,{\rm d}t = \frac{ A}{-\rm j2\pi f}\left[ {\rm e}^{-{\rm j}2\pi ft}\right]_{-T/2}^{+T/2} \\ & = \frac{\it A}{-\rm j 2\pi f}\left[\cos({\rm \pi} f T)-{\rm j} \cdot \sin({\rm \pi} fT)-\cos({\rm \pi} fT)-{\rm j} \cdot \sin({\rm \pi} fT)\right]. \end{align*}$$

$$\Rightarrow X(f)=A\cdot \frac{\sin({\rm \pi} fT)}{{\rm \pi} f}.$$

Erweitert man Zähler und Nenner mit $T$, so erhält man:

Fouriertransformation

Das Spektrum $X(f)$ eines Signals $x(t)$ lautet gemäß dem „Ersten Fourierintegral”:

$$X(f)= \hspace{0.05cm}\int _{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$

Wie auf der letzten Seite an einem einfachen Beispiel gezeigt wurde, ist dieses Integral bei einem energiebegrenzten Signal $x(t)$ problemlos lösbar. Bei nicht energiebegrenzten Signalen, zum Beispiel

• einem Gleichsignal (vgl. Kapitel 2.2),
• einer harmonischen Schwingung (vgl. Kapitel 2.3),
• einem anklingenden Signal,

divergiert aber das Fourierintegral. Unter Einbeziehung einer beidseitig abfallenden Hilfsfunkion $\epsilon (t)$ kann allerdings die Konvergenz erzwungen werden:

$$X(f) = \lim_{\varepsilon \to 0} \int _{-\infty} ^{{+}\infty} x(t) \cdot {\rm e}^{\it -\varepsilon | \hspace{0.01cm} t \hspace{0.01cm} |} \cdot {\rm e}^{{-\rm j 2 \pi}\it ft} \,{\rm d}t.$$

Solche nicht energiebegrenzten Signale führen im Spektrum zu Diracfunktionen, manchmal auch „Distributionen” genannt. Man bezeichnet diesen allgemeinen Funktionalzusammenhang $X(f) = F[x(t)]$ als Fouriertransformation und verwendet hierfür die Kurzschreibweise:

$$X(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,x(t).$$

Bei einem anklingenden Signal wird die Konvergenz allerdings nur dann erreicht, solange die Zeitfunktion weniger als exponentiell ansteigt.

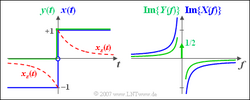
Wir betrachten eine akausale Sprungfunktion $x(t)$ = sign($t$) mit $x(t)$ = –1 für negative sowie $x(t)$ = +1 für positive Zeiten. Dieses Signal ist in nachfolgender Skizze links in blauer Farbe dargestellt.

Da das Signal $x(t)$ nach beiden Seiten bis ins Unendliche reicht, muss zur Berechnung der Fouriertransformierten für beide Abschnitte zunächst ein geeigneter Konvergenzfaktor $\text{e}^{-\epsilon |t|}$ hinzugefügt werden (es gelte $\epsilon > 0$). Die resultierende Zeitfunktion lautet dann:

$$x_\varepsilon (t) = \left\{ {\begin{array}{*{20}c} {{\rm{e}}^{ - \varepsilon t} } & {{\rm{f\ddot{u}r}}\quad t > 0,} \\ {{\rm{ - e}}^{\varepsilon t} } & {{\rm{f\ddot{u}r}}\quad t < 0.} \\\end{array}} \right.$$

Ähnlich wie auf der Seite Diracfunktion ergibt sich für die zugehörige Spektralfunktion

$$X_\varepsilon (f) = \frac{1}{{\varepsilon + {\rm{j}}2{\rm{\pi }}f}} - \frac{1}{{\varepsilon - {\rm{j}}2{\rm{\pi }}f}} = \frac{{ - {\rm{j4\pi }}f}}{{\varepsilon ^2 + \left( {2{\rm{\pi }}f} \right)^2 }}.$$

Eigentlich interessieren wir uns aber für das Spektrum der Sprungfunktion. Für diese gilt:

$$x(t) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm}\to \hspace{0.05cm}0 } x_\varepsilon (t).$$

Deshalb ist auch die Spektralfunktion $X(f)$ =F[$x(t)$] als Grenzwert von $X_\epsilon (f)$ für$\epsilon \to 0$ zu bestimmen:

$$X(f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 } X_\varepsilon (f) = \frac{{ - {\rm{j}}}}{{{\rm{\pi }}f}} = \frac{1}{{{\rm{j\pi }}f}}.$$

In der rechten Grafik ist die rein imaginäre Spektralfunktion $X(f)$ als blaue Kurve dargestellt. Man erkennt, dass mit zunehmender Frequenz $|X(f)|$ kontinuierlich abnimmt. Der grüne Kurvenzug in der linken Grafik zeigt das Signal $y(t)$, das sich von $x(t)$ nur bei den negativen Zeiten unterscheidet. In diesem Bereich gilt $y(t)$ = 0. Die zugehörige Spektralfunktion $Y(f)$ ist im gesamten Bereich nur halb so groß wie $X(f)$. Dies zeigt die nachfolgende Rechnung:

$$Y(f) = \mathop {\lim }\limits_{\varepsilon \to 0 } Y_\varepsilon (f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 }\frac{1}{{\varepsilon + {\rm{j}}2{\rm{\pi }}f}} = \frac{1}{{{\rm{j2\pi }}f}}.$$

Zudem ergibt sich auf Grund des Gleichanteils nun noch eine Diracfunktion bei $f$ = 0 mit dem Gewicht 1/2. Hierauf wird im Beispiel zum Abschnitt Zuordnungssatz (Kapitel 3.3) noch im Detail eingegangen.

Das zweiter Fourierintegral

Bisher haben wir lediglich gezeigt, wie man für ein aperiodisches, impulsförmiges Signal $x(t)$ die zugehörige Spektralfunktion $X(f)$ berechnet. Nun wenden wir uns der umgekehrten Aufgabe zu, aus der Spektralfunktion $X(f)$ die Zeitfunktion $x(t)$ zu ermitteln.

Mit den gleichen Bezeichnungen wie auf den ersten Seiten dieses Kapitels kann man das Signal $x(t)$ als Fourierreihe schreiben, wobei nun der Grenzübergang $f_0' \to 0$ zu berücksichtigen ist:

$$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty}{D_{\it \nu}}' \cdot \rm e^{j 2 \pi \it\nu {f_{\rm 0}}' t}.$$

Erweitert man nun sowohl den Zähler als auch den Nenner um $f_0'$, so erhält man:

$$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty} ({{D_{\it \nu}}'}/{{f_{\rm 0}}'}) \cdot \rm e^{j 2 \pi \it \nu {f_{\rm 0}}' t} \cdot {\it f_{\rm 0}}'.$$

Der Grenzübergang $f_0' \to 0$ hat nun folgende Auswirkungen:

• Die (unendliche) Summe wird zu einem Integral, wobei $f_0'$ formal durch die differenzielle Größe d$f$ (Integrationsvariable) zu ersetzen ist.
• Die Größe $v \cdot f_0'$ im Exponenten beschreibt die physikalische Frequenz $f$.
• Der Quotient $D_v'/f_0'$ ergibt die Spektralfunktion $X(f)$ bei der Frequenz $f$.

Unter Berücksichtigung dieser Eigenschaften kommt man zum zweiten Fourierintegral.

Ist die Spektralfunktion $X(f)$ eines aperiodischen und energiebegrenzten Signals gegeben, so lautet die dazugehörige Zeitfunktion:

$$x(t) = \hspace{0.01cm}\int_{-\infty} ^{{+}\infty} X(f) \, \cdot \, { \rm e}^{\rm j 2\pi \it ft} \,{\rm d}f$$

⇒ Zweites Fourierintegral.