Aufgaben:Aufgabe 2.7Z: Kohärenzbandbreite des LZI–Zweiwegekanals

• Zurück zum Buch

Zweiwegekanäle

Zum GWSSUS–Modell werden zwei Kenngrößen angegeben, die beide die entstehende Verzögerung $\tau$ statistisch erfassen. Mehr Informationen zum Thema „Mehrwegeausbreitung” finden Sie auf Seite 8 des Theorieteils.

• Die Mehrwegeverbreiterung $T_{\rm V}$ ist definitionsgemäß gleich der Standardabweichung der Zufallsgröße $\tau$. Diese kann aus der Wahrscheinlichkeitsdichte $f_{\rm V}(\tau)$ ermittelt werden. Die WDF $f_{\rm V}(\tau)$ ist dabei formgleich mit dem Verzögerungs–Leistungsdichtespektrum ${\it \Phi}_{\rm V}(\tau)$ ist.
• Die Kohärenzbandbreite $B_{\rm K}$ beschreibt den gleichen Sachverhalt im Frequenzbereich. Diese ist implizit durch die Frequenzkorrelationsfunktion $\varphi_{\rm F}(\Delta f)$ festgelegt als derjenige $\Delta f$–Wert, bei dem deren Betrag erstmals auf die Hälfte abgefallen ist:

$$|\varphi_{\rm F}(\Delta f = B_{\rm K})| \stackrel {!}{=} \frac{1}{2} \cdot |\varphi_{\rm F}(\Delta f = 0)| \hspace{0.05cm}.$$

Der Zusammenhang zwischen ${\it \Phi}_{\rm V}(\tau)$ und $\varphi_{\rm F}(\Delta f)$ ist durch die Fouriertransformation gegeben:

$$\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}.$$

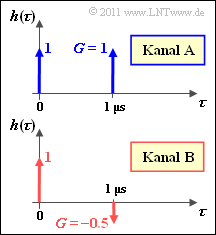
Beide Definitionen sind bei einem zeitinvarianten Kanal nur bedingt geeignet. Beispielsweise verwendet man für einen zeitinvarianten Zweiwegekanal (also mit konstanten Pfadgewichten entsprechend obiger Grafik) oft als Näherung für die Kohärenzbandbreite:

$$B_{\rm K}\hspace{0.05cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$

In dieser Aufgabe soll geklärt werden,

• warum es in der Literatur verschiedene Definitionen für die Kohärenzbandbreite gibt,
• welcher Zusammenhang zwischen $B_{\rm K}$ und $B_{\rm K}'$ besteht, und
• welche Definitionen bei welchen Randbedingungen sinnvoll sind.

Hinweis:

• Die Aufgabe bezieht sich auf einige Theorieseiten im Kapitel Mehrwegeempfang beim Mobilfunk und im Kapitel Das GWSSUS–Kanalmodell.

Fragebogen

1

Welche Kohärenzbandbreitennäherungen ergeben sich für Kanal A und B?

${\rm Kanal A} \text {:} \hspace{0.4cm} B_{\rm K}' \ = \ $ $\ \rm kHz$

${\rm Kanal B} \text {:} \hspace{0.4cm} B_{\rm K}' \ = \ $ $\ \rm kHz$

2

Wie lautet die WDF $f_{\rm V}(\tau)$? $G$ gibt das Gewicht des zweiten Pfades an.

	$f_{\rm V}(\tau) = \delta(\tau) + G \cdot \delta(\tau \, –\tau_0)$,
	$f_{\rm V}(\tau) = \delta(\tau) + G^2 \cdot \delta(\tau \, –\tau_0)$,
	$f_{\rm V}(\tau) = 1/(1 + G^2) \cdot \delta(\tau) + G^2/(1 + G^2) \cdot \delta(\tau \, –\tau_0)$.

3

Berechnen Sie die Mehrwegeverbreitung.

${\rm Kanal \ A} \text{:} \hspace{0.4cm} T_{\rm V} \ = \ $ $\ \rm \mu s$

${\rm Kanal \ B} \text{:} \hspace{0.4cm} T_{\rm V} \ = \ $ $\ \rm \mu s$

4

Welche Kohärenzbandbreite $B_{\rm K}$ weist der Kanal A auf?

	Es gilt $B_{\rm K} = 333 \ \rm kHz$.
	Es gilt $B_{\rm K} = 500 \ \rm kHz$.
	Es gilt $B_{\rm K} = 1 \ \rm MHz$.
	$B_{\rm K}$ ist nach dieser Definition nicht angebbar.

5

Welche Kohärenzbandbreite $B_{\rm K}$ weist der Kanal B auf?

	Es gilt $B_{\rm K} = 333 \ \rm kHz$.
	Es gilt $B_{\rm K} = 500 \ \rm kHz$.
	Es gilt $B_{\rm K} = 1 \ \rm MHz$.
	$B_{\rm K}$ ist nach dieser Definition nicht angebbar.

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)