Aufgaben:Aufgabe 1.3: Kanalmodelle BSC–BEC–BSEC–AWGN: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
Wael (Diskussion | Beiträge) |
||
| Zeile 5: | Zeile 5: | ||
[[Datei:P_ID2383__KC_A_1_3_neu.png|right|frame|BEEC und dessen Bezug zum AWGN–Modell]] | [[Datei:P_ID2383__KC_A_1_3_neu.png|right|frame|BEEC und dessen Bezug zum AWGN–Modell]] | ||
Im Theorieteil zu diesem Kapitel werden die folgenden digitalen Kanalmodelle behandelt: | Im Theorieteil zu diesem Kapitel werden die folgenden digitalen Kanalmodelle behandelt: | ||
| + | *[[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|Binary Symmetric Channel]](BSC), | ||
| + | *[[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Erasure_Channel_.E2.80.93_BEC|Binary Erasure Channel]](BEC), | ||
| + | *[[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Error_.26_Erasure_Channel_.E2.80.93_BSEC|Binary Symm. Error & Erasure Ch.]](BSEC). | ||
| + | Die obere Grafik zeigt das BSEC–Modell. Daraus lassen sich auch die beiden anderen Kanalmodelle ableiten: | ||
| + | *Mit λ = 0 ergibt sich das BSC–Modell. | ||
| + | *Mit $\varepsilon = 0$ ergibt sich das BEC–Modell. | ||
| + | Die untere Grafik zeigt den Zusammenhang zwischen dem BSEC–Modell und dem analogen AWGN–Kanal- modell. Um Verwechslungen zu vermeiden, bezeichnen wir das (analoge) Ausgangssignal des AWGN–Kanals mit yA, wobei mit dem Rauschterm n gilt: yA = ''x̃'' + n. | ||
| + | Die Tilde weist auf die bipolare Beschreibung des Digitalsignals hin. Es gilt ''x̃'' = +1, falls x = 0, und ''x̃'' = –1, falls x = 1. | ||
| + | |||
| + | Man erkennt die ternäre Ausgangsgröße y ∈ {0, 1, E}, die sich aus dem AWGN–Modell durch die Unterteilung in drei Bereiche ergibt. Hierzu werden die Entscheiderschwellen G0 und G1 benötigt. | ||
| + | |||
| + | y = E (Erasure) sagt aus, dass die Entscheidung so unsicher ist, dass als Ergebnis weder y = 0 noch y = 1 gerechtfertigt erscheint. In deutschen Fachbüchern spricht man von einer ''Auslöschung''. | ||
| + | ''Hinweis:'' | ||
| + | Die Aufgabe bezieht sich auf das Kapitel 1.2. Die Streuung des AWGN–Rauschens n wird für die gesamte Aufgabe zu σ = 0.4 angenommen. Die Wahrscheinlichkeit, dass die Zufallsgröße n größer ist als A oder kleiner als –A, ergibt sich mit dem komplementären Gaußschen Fehlerintegral Q(x) wie folgt: | ||
| + | :$${\rm Pr}(n > A) = {\rm Pr}(n < -A) = {\rm Q}(A/\sigma)\hspace{0.05cm}.$$ | ||
| + | Es folgen noch einige Zahlenwerte der Q–Funktion: | ||
| + | :$$ {\rm Q}(0) \hspace{-0.1cm} = \hspace{-0.1cm} 50\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(0.5) = 30.85\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1) = 15.87\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1.5) = 6.68\%\hspace{0.05cm},\\ {\rm Q}(2) \hspace{-0.1cm} = \hspace{-0.1cm} 2.28\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.5) = 0.62\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3) = 0.14\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3.5) = 0.02\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(4) \approx 0 \hspace{0.05cm}.$$ | ||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 27. November 2017, 15:32 Uhr
Im Theorieteil zu diesem Kapitel werden die folgenden digitalen Kanalmodelle behandelt:
- Binary Symmetric Channel(BSC),
- Binary Erasure Channel(BEC),
- Binary Symm. Error & Erasure Ch.(BSEC).
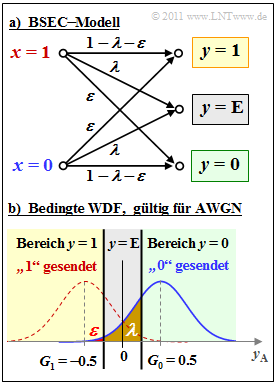
Die obere Grafik zeigt das BSEC–Modell. Daraus lassen sich auch die beiden anderen Kanalmodelle ableiten:
- Mit λ = 0 ergibt sich das BSC–Modell.
- Mit $\varepsilon = 0$ ergibt sich das BEC–Modell.
Die untere Grafik zeigt den Zusammenhang zwischen dem BSEC–Modell und dem analogen AWGN–Kanal- modell. Um Verwechslungen zu vermeiden, bezeichnen wir das (analoge) Ausgangssignal des AWGN–Kanals mit yA, wobei mit dem Rauschterm n gilt: yA = x̃ + n.
Die Tilde weist auf die bipolare Beschreibung des Digitalsignals hin. Es gilt x̃ = +1, falls x = 0, und x̃ = –1, falls x = 1.
Man erkennt die ternäre Ausgangsgröße y ∈ {0, 1, E}, die sich aus dem AWGN–Modell durch die Unterteilung in drei Bereiche ergibt. Hierzu werden die Entscheiderschwellen G0 und G1 benötigt.
y = E (Erasure) sagt aus, dass die Entscheidung so unsicher ist, dass als Ergebnis weder y = 0 noch y = 1 gerechtfertigt erscheint. In deutschen Fachbüchern spricht man von einer Auslöschung. Hinweis: Die Aufgabe bezieht sich auf das Kapitel 1.2. Die Streuung des AWGN–Rauschens n wird für die gesamte Aufgabe zu σ = 0.4 angenommen. Die Wahrscheinlichkeit, dass die Zufallsgröße n größer ist als A oder kleiner als –A, ergibt sich mit dem komplementären Gaußschen Fehlerintegral Q(x) wie folgt:
- $${\rm Pr}(n > A) = {\rm Pr}(n < -A) = {\rm Q}(A/\sigma)\hspace{0.05cm}.$$
Es folgen noch einige Zahlenwerte der Q–Funktion:
- $$ {\rm Q}(0) \hspace{-0.1cm} = \hspace{-0.1cm} 50\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(0.5) = 30.85\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1) = 15.87\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(1.5) = 6.68\%\hspace{0.05cm},\\ {\rm Q}(2) \hspace{-0.1cm} = \hspace{-0.1cm} 2.28\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.5) = 0.62\%\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3) = 0.14\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(3.5) = 0.02\% \hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(4) \approx 0 \hspace{0.05cm}.$$
Fragebogen
Musterlösung