Aufgaben:Aufgabe 3.6Z: Übergangsdiagramm bei 3 Zuständen

• Zurück zum Buch

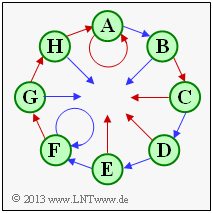
Im Zustandsübergangsdiagramm eines Codierers mit Gedächtnis $m$ gibt es $2^m$ Zustände. Das dargestellte Diagramm mit acht Zuständen beschreibt deshalb einen Faltungscoder mit dem Gedächtnis $m = 3$.

Normalerweise bezeichnet man die Zustände mit $S_0, \ ... , \ S_{\mu}, \ ... \ , \ S_7$, wobei der Index $\mu$ aus der Belegung des Schieberegisters (Inhalt von links nach rechts: $u_{i–1}, u_{i–2}, u_{i–3})$ festgelegt ist:

$$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2\hspace{0.03cm}^{l-1} \cdot u_{i-l} \hspace{0.05cm}.$$

Der Zustand $S_0$ ergibt sich deshalb für den Schieberegisterinhalt „$000$”, der Zustand $S_1$ für „$100$” und der Zustand $S_7$ für „$111$”.

In obiger Grafik sind allerdings für die Zustände $S_0, \, ... \, , \, S_7$ Platzhalter names $\mathbf{A}, \, ... \, , \, \mathbf{H}$ verwendet. In den Teilaufgaben (1) und (2) sollen Sie klären, welcher Platzhalter für welchen Zustand steht.

Bei Faltungscodierer der Rate $1/n$, die her ausschließlich betrachtet werden sollen, gehen von jedem Zustand $S_{\mu}$ zwei Pfeile ab, ein roter für das aktuelle Informationsbit $u_i = 0$ und ein blauer für $u_i = 1$. Auch deshalb ist das gezeigte Zustandsübergangsdiagramm nicht vollständig.

Zu erwähnen ist weiterhin:

• Bei jedem Zustand kommen auch zwei Pfeile an, wobei diese durchaus gleichfarbig sein können.
• Neben den Pfeilen stehen üblicherweise noch die $n$ Codebits. Auch hierauf wurde hier verzichtet.

Hinweise:

• Die Aufgabe bezieht sich auf die beiden ersten Seiten des Kapitels Codebeschreibung mit Zustands– und Trellisdiagramm.
• In der Aufgabe Z3.7 werden zwei Faltungscodes mit Gedächtnis $m = 3$ untersucht, die beide durch das hier analysierte Zustandsübergangsdiagramm beschrieben werden können.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Für welche Zustände $S_{\mu}$ stehen die Platzhalter $\mathbf{A}$ und $\mathbf{F}$? ⇒ Index eingeben.

${\rm Zustand \} \mathbf{A} \ ⇒ \ Index \ {\mu} \ = \ $

${\rm Zustand \} \mathbf{F} \ ⇒ \ Index \ {\mu} \ = \ $

2

Nennen Sie auch die Zuordnungen der anderen Platzhalter zu den Indizes.

${\rm Zustand \} \mathbf{B} \ ⇒ \ Index \ {\mu} \ = \ $

${\rm Zustand \} \mathbf{C} \ ⇒ \ Index \ {\mu} \ = \ $

${\rm Zustand \} \mathbf{D} \ ⇒ \ Index \ {\mu} \ = \ $

${\rm Zustand \} \mathbf{E} \ ⇒ \ Index \ {\mu} \ = \ $

${\rm Zustand \} \mathbf{G} \ ⇒ \ Index \ {\mu} \ = \ $

${\rm Zustand \} \mathbf{H} \ ⇒ \ Index \ {\mu} \ = \ $

3

Zu welchem Zustand $S_{\mu}$ geht der jeweils zweite Pfeil?  ⇒  Index eingeben.

${\rm Von \ S_{\rm 1} \ zum \ Zustand \ mit \ Index \ {\mu} \ = \ $

${\rm Von \ S_{\rm 3} \ zum \ Zustand \ mit \ Index \ {\mu} \ = \ $

${\rm Von \ S_{\rm 5} \ zum \ Zustand \ mit \ Index \ {\mu} \ = \ $

${\rm Von \ S_{\rm 7} \ zum \ Zustand \ mit \ Index \ {\mu} \ = \ $

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)