Aufgaben:Aufgabe 1.14: Bhattacharyya–Schranke für BEC

• Zurück zum Buch

Mögliche Empfangsvektoren für (5, 2)–Code und BEC

Wir betrachten in dieser Aufgabe den systematischen (5, 2)–Code mit der 2×5–Generatormatrix

$${ \boldsymbol{\rm G}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &1 &0\\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm},$$

der 3 × 5–Prüfmatrix

$${ \boldsymbol{\rm H}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},$$

und den $2^k = 4$ Codeworten

$$\underline{x}_0 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_1 = (0, 1, 0, 1, 1)\hspace{0.05cm},$$

$$\underline{x}_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_3 = (1, 1, 1, 0, 1)\hspace{0.05cm}.$$

Am Ausgang des digitalen Kanals, der durch das BEC–Modell (Binary Erasure Channel) mit der Auslöschungswahrscheinlichkeit $\lambda = 0.001$ festgelegt wird, tritt der Empfangsvektor

$$\underline{y} = (y_1, \hspace{0.05cm}y_2, \hspace{0.05cm}y_3, \hspace{0.05cm}y_4, \hspace{0.05cm}y_5)$$

auf, wobei für $i = 1, ... , 5$ gilt: $y_{i} \in$ {0, 1, E}. Der BEC–Kanal zeichnet sich dadurch aus, dass

• Verfälschungen (0 → 1, 1 → 0) ausgeschlossen sind,
• es aber zu Auslöschungen (0 → E, 1 → E) kommen kann.

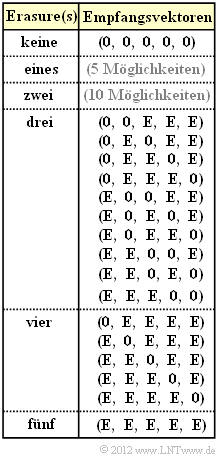
Die Grafik zeigt explizit alle möglichen Empfangsvektoren y mit drei oder mehr Auslöschungen (englisch: Erasures, abgekürzt E) unter der Voraussetzung, dass der Nullvektor (0, 0, 0, 0, 0) gesendet wurde. Bei weniger als drei Auslöschungen liefert bei dem betrachteten (5, 2)–Code der Codewortschätzer immer die richtige Entscheidung: $\underline{z} = \underline{x}$.

Bei drei oder mehr Auslöschungen kann es dagegen zu Fehlentscheidungen kommen. In diesem Fall gilt für die Blockfehlerwahrscheinlichkeit

$$ {\rm Pr(Blockfehler)}= {\rm Pr} (\underline{z} \ne \underline{x}) = {\rm Pr}\left \{ \hspace{0.1cm} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}\cup \hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \hspace{0.1cm}\right \} \hspace{0.05cm}.$$

Das Ereignis $[\underline{x}_{0} → \underline{x}_{1}]$ sagt nicht unbedingt aus, dass beim betrachteten Empfangsvektor y tatsächlich für das Codewort $\underline{x}_{1}$ entschieden wird, sondern lediglich, dass die Entscheidung für $x_{1}$ aufgrund der Statistik sinnvoller wäre als die Entscheidung für $\underline{x}_{0}$. Es könnte aber auch für $\underline{x}_{2}$ oder $\underline{x}_{3}$ entschieden werden, wenn das Maximum–Likelihood–Kriterium hierfür spricht. Die Berechnung der Blockfehlerwahrscheinlichkeit ist schwierig, da die Ereignisse $[\underline{x}_{0} → \underline{x}_{1}]$ , $[\underline{x}_{0} → \underline{x}_{2}]$ und $[\underline{x}_{0} → \underline{x}_{3}]$ nicht notwendigerweise disjunkt sind. Eine obere Schranke liefert die Union Bound:

$${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$

Eine weitere Schranke wurde von Bhattacharyya angegeben:

$${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr(Blockfehler)} \hspace{0.05cm},$$

wobei beim Binary Erasure Channel $\beta = \lambda$ gilt. W(X) ist die Gewichtsfunktion, wobei die Pseudo–Variable X hier durch den Bhattacharyya–Parameter $\lambda$ zu ersetzen ist. Die Bhattacharyya–Schranke liegt je nach Kanal mehr oder weniger weit oberhalb der Union Bound. Ihre Bedeutung liegt darin, dass die Schranke für unterschiedliche Kanäle in gleicher Weise angebbar ist.

Hinweis:

Die Aufgabe gehört zum Themengebiet von Kapitel Schranken für die Blockfehlerwahrscheinlichkeit.

Fragebogen

1

Wie groß ist die paarweise Fehlerwahrscheinlichkeit zwischen den Codeworten $\underline{x}_{0} = (0, 0, 0, 0, 0)$ und $\underline{x}_{1} = (0, 1, 0, 1, 1)$?

$\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ $\ \cdot 10^{-4} $

2

Welche Aussagen stimmen bezüglich ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ mit Laufindex $i = 1, ... , 3$? Hierbei bezeichnet $d_{\rm H}$ die Hamming–Distanz zwischen $x_{0}$ und $x_{i}$.

	Es gilt ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ \lambda ^{d_{\rm H}} \ · \ (1 – \lambda)^{n – d_{\rm H}}$.
	Es gilt ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ 1/2 · \lambda ^{d_{\rm H}}.$
	${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ ist die Verfälschungswahrscheinlichkeit von $x_{0}$ nach $x_{i}$.

3

Wie groß sind die Wahrscheinlichkeiten

$\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{2}]$ $\ \cdot 10^{-4} $

$\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{3}]$ $\ \cdot 10^{-5} $

4

Geben Sie die Union Bound für die Blockfehlerwahrscheinlichkeit an.

$\ {\rm Pr(Union Bound)}$ $\ \cdot 10^{-3} $

5

Wie lautet im vorliegenden Fall die Bhattacharyya–Schranke?

$\ {\rm Pr(Bhattacharyya)}$ $\ \cdot 10^{-3} $

Musterlösung

Musterlösung

1. 2. 3. 4. 5. 6. 7.