Aufgaben:Aufgabe 2.4: GF(2 hoch 2)–Darstellungsformen: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 48: | Zeile 48: | ||
- Zwischen beiden Darstellungen besteht keinerlei Zusammenhang. | - Zwischen beiden Darstellungen besteht keinerlei Zusammenhang. | ||
| − | {Wie hängen Polynom– und | + | {Wie hängen Polynom– und Exponentendarstellung zusammen? |
|type="[]"} | |type="[]"} | ||
- Es sind keine Zusammenhänge erkennbar. | - Es sind keine Zusammenhänge erkennbar. | ||
+ Die Elemente $0, \ 1$ und $\alpha$ sind in beiden Darstellungen gleich. | + Die Elemente $0, \ 1$ und $\alpha$ sind in beiden Darstellungen gleich. | ||
| − | + Das Element $1 + \alpha$ lautet in der | + | + Das Element $1 + \alpha$ lautet in der Exponentendarstellung $\alpha^2$. |
| − | - Das Element $\alpha^2$ der | + | - Das Element $\alpha^2$ der Exponentendarstellung steht für $\alpha \cdot (1 + \alpha)$. |
{Berechnen Sie die Ausdrücke $A$ und $B$ nach diesen drei Darstellungsformen. Welche Aussagen treffen zu? | {Berechnen Sie die Ausdrücke $A$ und $B$ nach diesen drei Darstellungsformen. Welche Aussagen treffen zu? | ||
Version vom 15. Dezember 2017, 17:33 Uhr
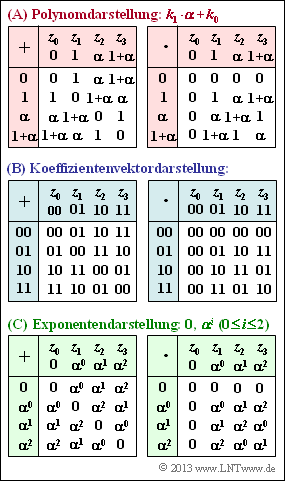
Nebenstehend sehen Sie für den Erweiterungskörper $\rm GF(2^2)$ die Additions– sowie die Multiplikationstabelle in drei verschiedenen Varianten:
- die Polynomdarstellung,
- die Koeffizientenvektordarstellung,
- die Exponentendarstellung.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Erweiterungskörper.
- Alle notwendigen Informationen zu ${\rm GF}(2^2)$ finden Sie auf der Seite 1 dieses Kapitels.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)