Aufgabe 2.6: Zyklisches Präfix

• Zurück zum Buch

DSL/DMT mit zyklischem Präfix

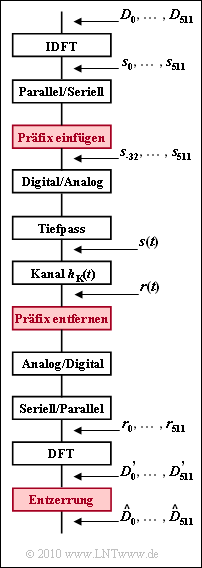
Ein wesentlicher Vorteil von DSL/DMT ist die einfache Entzerrung von Kanalverzerrungen durch die Einfügung eines Guard–Intervalls und eines zyklischen Präfix. Die Grafik zeigt ein vereinfachendes Blockschaltbild, wobei die zur Entzerrung des Kanalfrequenzgangs

$$H_{\rm K}(f) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm K}(t)$$

erforderlichen Komponenten rot hervorgehoben sind.

Für den ADSL/DMT–Downstream gelten folgende Parameter:

• Mit jedem Rahmen werden die Subkanäle $k = 64, ... , 255$ bei den Trägerfrequenzen $f_k = k \cdot f_0$ mit den QAM–Symbolen $D_k$ belegt. Wegen der Reservierung der untersten Frequenzen für ISDN und Upstream gilt $D_0 = ... D_{63} = 0$.

• Die Grundfrequenz ist zu $f_0 = 4.3125 \ \rm kHz$ gewählt und die Rahmendauer beträgt $T = 1/f_0 \approx 232 \ {\rm\mu s}$. Diese Werte ergeben sich aus der Forderung, dass pro Sekunde $4000$ Rahmen übertragen werden sollen und nach jedem $68$. Rahmen ein Synchronisationsrahmen eingefügt wird.

• Nach Belegung der oberen Koeffizienten $(k = 257, ... , 448)$ gemäß $D_k = D_{512–k}^{\ast}$ wird der gesamte Block $D_0, ... , D_{511}$ einer Inversen Diskreten Fouriertransformation (IDFT) zugeführt. Die Zeitkoeffizienten sind dann $s_0, ... , s_{511}$.

• Um Impulsinterferenzen – auch Inter–Symbol–Interferenzen (ISI) genannt – zwischen benachbarten Rahmen zu vermeiden, wird zwischen zwei Rahmen ein Schutzabstand („Guard–Intervall”) der Dauer $T_{\rm G}$ eingefügt. Der Rahmenabstand muss dabei mindestens so groß sein wie die Länge $T_{\rm K}$der Impulsantwort.

• Zudem werden die IDFT–Ausgangswerte $(s_{480}, ... , s_{511})$ dupliziert, als $(s_{–32}, ..., s_{–1})$ dem Ausgangsvektor $(s_0, ... , s_{511})$ vorangestellt und im Guard–Intervall übertragen. Man nennt dies das „zyklische Präfix”. Somit stören sich auch die Subträger eines Rahmens nicht, das heißt, es gibt nicht nur keine ISI, sondern auch keine Inter–Carrier–Interferenzen (ICI).

Hinweis:

Die Aufgabe bezeiht sich auf die letzte Seite von Kapitel 2.4. Im Fragebogen bezeichnet $s_k(t)$ den (zeitkontinuierlichen) Signalverlauf, wenn allein der Koeffizient $D_k$ des Trägers bei $f_k = k \cdot f_0$ von $0$ verschieden ist.

Fragebogen

1

Wie groß ist die Dauer des Guard–Intervalls zu wählen?

$T_{\rm G} \ = \ $ $ \ \rm \mu s$

2

Welche Ausdehnung darf die Kanalimpulsantwort $h_{\rm K}(t)$ haben, damit es keine Intersymbolinterferenzen gibt?

$T_{\rm K, \ max} \ = \ $ $ \ \rm \mu s$

3

Welche Eigenschaften besitzt das DMT–System mit zyklischem Präfix? Der Einfluss des Rauschens soll hier unberücksichtigt bleiben.

	Alle Spektralkoeffizienten nach der DFT $(D_k')$ sind gleich $D_k$.
	Die Koeffizienten nach Entzerrung ($D_k$ mit ^) sind gleich $D_k$.
	Das Guard–Intervall hat keine Auswirkung auf die Datenrate.

4

Was wäre, wenn man das Guard–Intervall unbelegt lässt?

	Das würde nichts verbessern.
	Daten verschiedener Rahmen stören sich nicht gegenseitig.
	Daten innerhalb eines Rahmens stören sich nicht gegenseitig.

5

Auf welchem Prinzip beruht das zyklische Präfix?

	Der Einfluss von $h_K(t)$ wird auf $t < 0$ begrenzt.
	Für $0 ≤ t ≤ T$ stellt $s_k(t)$ eine harmonische Schwingung dar.
	$h_{\rm K}(t)$ hat keinen Einfluss auf Betrag und Phase von $s_k(t)$.

Musterlösung

Musterlösung

(1)  Innerhalb des Guard–Intervalls müssen beim Sender $32$ zusätzliche Abtastwerte $s_{–32}, ... , s_{–1}$ eingefügt werden. Damit gilt:

$$T_{\rm G} = \frac{32}{512} \cdot T = \frac{232\,{\rm \mu s}}{16} \hspace{0.15cm}\underline{= 14.5\,{\rm \mu s} }\hspace{0.05cm}.$$

(2)  ntersymbolinterferenzen (ISI) und Intercarrierinterferenzen (ICI) werden vermieden, so lange die Länge $T_{\rm K}$ der Kanalimpulsantwort nicht größer ist als die Länge des Guard–Intervalls:

$$T_{\rm K,\hspace{0.08cm} max} \ge T_{\rm G} \hspace{0.15cm}\underline{= 14.5\,{\rm \mu s}} \hspace{0.05cm}.$$

(3)  Richtig ist der Lösungsvorschlag 2. Für die Ausgangskoeffizienten der DFT gilt im rauschfreien Fall:

$$D_k' = D_k \cdot H_{\rm K} ( f = f_k), \hspace{0.2cm} f_k = k \cdot f_0 \hspace{0.05cm}.$$

Die einzelnen Subkanäle können einzeln durch Multiplikation mit $H_{\rm K}^{–1}(f = f_k)$ entzerrt werden. Damit gilt für alle $k = 1, ... , K$:

$$\hat{D}_k = D_k \hspace{0.05cm}.$$

Die letzte Aussage ist falsch. Die Rate ist vielmehr um den Faktor $T/(T + T_{\rm G}) = 16/17$ geringer als ohne Guard–Intervall und zyklischem Präfix. Dieser geringe Verlust wird aber gerne in Kauf genommen, da die einfache Entzerrung diesen Nachteil mehr als ausgleicht.

(4)  Richtig ist hier nur der zweite Lösungsvorschlag. Nicht verhindert würden dadurch so genannte Intercarrierinterferenzen, das heißt, die Subträger eines Rahmens wären dann nicht mehr orthogonal zueinander, da die Faltung der zeitlich auf $T$ begrenzten harmonischen Schwingung mit der Impulsantwort keine si–Funktion ergibt, wie dies bei idealem Kanal der Fall ist. Damit beeinflusst der Koeffizient $D_k$ bei $k \cdot f_0$ auch die Spektralwerte bei $\kappa \cdot f_0$ in der Umgebung $(\kappa \neq k)$.

(5)  Richtig sind die beiden ersten Lösungsvorschläge. Betrag und Phase von $s_k(t)$ wird sehr wohl durch $h_{\rm K}(t)$ verändert, und zwar entsprechend dem Wert $H_{\rm K}(f = f_k)$ des Frequenzgangs. Durch den Entzerrer auf der Empfängerseite lässt sich dieser Fehler aber in einfacher Weise (und unabhängig von den anderen Subkanälen) korrigieren.