Aufgaben:Aufgabe 1.16Z: Schranken für die Gaußsche Fehlerfunktion: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
|||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Kanalcodierung/Schranken für die Blockfehlerwahrscheinlichkeit | + | {{quiz-Header|Buchseite=Kanalcodierung/Schranken für die Blockfehlerwahrscheinlichkeit}} |
| − | |||
| − | |||
| − | |||
| − | }} | ||
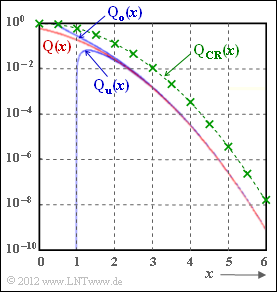
[[Datei:P_ID2415__KC_A_1_15.png|right|farme|Q(<i>x</i>) und verwandte Funktionen]] | [[Datei:P_ID2415__KC_A_1_15.png|right|farme|Q(<i>x</i>) und verwandte Funktionen]] | ||
| Zeile 17: | Zeile 13: | ||
${\rm Q}(x)$ ist eine monoton fallende Funktion mit ${\rm Q}(0) = 0.5$. Für große Werte von $x$ tendiert ${\rm Q}(x)$ gegen Null. | ${\rm Q}(x)$ ist eine monoton fallende Funktion mit ${\rm Q}(0) = 0.5$. Für große Werte von $x$ tendiert ${\rm Q}(x)$ gegen Null. | ||
| − | Das Integral der | + | Das Integral der ${\rm Q}$–Funktion ist analytisch nicht lösbar und wird meist in Tabellenform angegeben. Aus der Literatur bekannt sind aber handhabbare Näherungslösungen bzw. Schranken für positive $x$–Werte: |
*die obere Schranke (obere blaue Kurve in nebenstehender Grafik, nur gültig für $x > 0$): | *die obere Schranke (obere blaue Kurve in nebenstehender Grafik, nur gültig für $x > 0$): | ||
| Zeile 33: | Zeile 29: | ||
In der Aufgabe ist zu untersuchen, in wie weit diese Schranken als Näherungen für ${\rm Q}(x)$ herangezogen werden können und welche Verfälschungen sich dadurch ergeben. | In der Aufgabe ist zu untersuchen, in wie weit diese Schranken als Näherungen für ${\rm Q}(x)$ herangezogen werden können und welche Verfälschungen sich dadurch ergeben. | ||
| − | '' | + | ''Hinweise:'' |
| − | + | * Die Aufgabe bezieht sich auf das Kapitel [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit|Schranken für die Blockfehlerwahrscheinlichkeit]] dieses Buches sowie auf das Kapitel [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken|Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken]] im Buch „Stochastische Signaltheorie”. | |
| − | Die Aufgabe bezieht sich auf das Kapitel [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit|Schranken für die Blockfehlerwahrscheinlichkeit]] dieses Buches sowie auf das Kapitel [[Kanalcodierung/Distanzeigenschaften_und_Fehlerwahrscheinlichkeitsschranken|Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken]] im Buch „Stochastische Signaltheorie”. Die Aufgabe bietet auch einige wichtige Hinweise zur Lösung der [[Aufgaben:1.16_Schranken_für_AWGN|Aufgabe 1.16]], in der die Funktion ${\rm Q}_{\rm CR}(x)$ zur Herleitung der [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit#Die_obere_Schranke_nach_Bhattacharyya|Bhattacharyya–Schranke]] für den AWGN–Kanal benötigt wird. Weiter verweisen wir auf das folgende Interaktionsmodul: | + | * Die Aufgabe bietet auch einige wichtige Hinweise zur Lösung der [[Aufgaben:1.16_Schranken_für_AWGN|Aufgabe 1.16]], in der die Funktion ${\rm Q}_{\rm CR}(x)$ zur Herleitung der [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit#Die_obere_Schranke_nach_Bhattacharyya|Bhattacharyya–Schranke]] für den AWGN–Kanal benötigt wird. |
| + | * Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | * Weiter verweisen wir auf das folgende Interaktionsmodul: | ||
| + | # [[Komplementäre Gaußsche Fehlerfunktion]] | ||
| − | |||
Version vom 21. Dezember 2017, 11:15 Uhr
Die Wahrscheinlichkeit, dass eine Gaußsche Zufallsgröße $n$ mit Streuung $\sigma$ → Varianz $\sigma^2$ betragsmäßig größer ist als ein Wert $A$, ist gleich
- $${\rm Pr}(n > A) = {\rm Pr}(n < -A) ={\rm Q}(A/\sigma) \hspace{0.05cm}.$$
Hierbei verwendet ist eine der wichtigsten Funktionen für die Nachrichtentechnik (in der Grafik rot eingezeichnet): die Komplementäre Gaußsche Fehlerfunktion
- $$\rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int\limits_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm}.$$
${\rm Q}(x)$ ist eine monoton fallende Funktion mit ${\rm Q}(0) = 0.5$. Für große Werte von $x$ tendiert ${\rm Q}(x)$ gegen Null.
Das Integral der ${\rm Q}$–Funktion ist analytisch nicht lösbar und wird meist in Tabellenform angegeben. Aus der Literatur bekannt sind aber handhabbare Näherungslösungen bzw. Schranken für positive $x$–Werte:
- die obere Schranke (obere blaue Kurve in nebenstehender Grafik, nur gültig für $x > 0$):
- $$ \rm Q_o(\it x)=\frac{\rm 1}{\sqrt{\rm 2\pi}\cdot x}\cdot \rm e^{-\it x^{\rm 2}/\rm 2}\hspace{0.15cm} \ge \hspace{0.15cm} \rm Q (\it x) \hspace{0.05cm},$$
- die untere Schranke (untere blaue Kurve in der Grafik, nur gültig für $x > 1$):
- $$ \rm Q_u(\it x)=\frac{\rm 1-{\rm 1}/{\it x^{\rm 2}}}{\sqrt{\rm 2\pi}\cdot x}\cdot \rm e^{-\it x^{\rm 2}/\rm 2} \hspace{0.15cm} \le \hspace{0.15cm} \rm Q (\it x) \hspace{0.05cm},$$
- die Chernoff–Rubin–Schranke (grüne Kurve in der Grafik, gezeichnet für $K = 1$):
- $$\rm Q_{CR}(\it x)=K \cdot \rm e^{-\it x^{\rm 2}/\rm 2} \hspace{0.15cm} \ge \hspace{0.15cm} \rm Q (\it x) \hspace{0.05cm}.$$
In der Aufgabe ist zu untersuchen, in wie weit diese Schranken als Näherungen für ${\rm Q}(x)$ herangezogen werden können und welche Verfälschungen sich dadurch ergeben.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Schranken für die Blockfehlerwahrscheinlichkeit dieses Buches sowie auf das Kapitel Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken im Buch „Stochastische Signaltheorie”.
- Die Aufgabe bietet auch einige wichtige Hinweise zur Lösung der Aufgabe 1.16, in der die Funktion ${\rm Q}_{\rm CR}(x)$ zur Herleitung der Bhattacharyya–Schranke für den AWGN–Kanal benötigt wird.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Weiter verweisen wir auf das folgende Interaktionsmodul:
Fragebogen
Musterlösung
- $${\rm Q_o}(x)=\frac{1}{\sqrt{\rm 2\pi}\cdot x}\cdot {\rm e}^{-x^{\rm 2}/\rm 2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_o}(4 )=\frac{1}{\sqrt{\rm 2\pi}\cdot 4}\cdot {\rm e}^{-8 }\hspace{0.15cm}\underline{\approx 3.346 \cdot 10^{-5}}\hspace{0.05cm}.$$
Die untere Schranke kann wie folgt umgewandelt werden:
- $${\rm Q_u}( x)=(1-1/x^2) \cdot {\rm Q_o}(x) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_u}(4 ) \hspace{0.15cm}\underline{\approx 3.137 \cdot 10^{-5}} \hspace{0.05cm}.$$
Die relativen Abweichungen gegenüber dem „echten” Wert ${\rm Q}(4) = 3.167 · 10^{–5}$ sind $+5%$ bzw. $–1%.$
(2) Richtig sind Antwort 1 und 2. Für $x = 2$ wird der tatsächliche Funktionswert ${\rm Q}(x) = 2.275 · 10^{–2}$ begrenzt durch ${\rm Q}_{o}(x) = 2.7 · 10^{–2}$ bzw. ${\rm Q}_{u}(x) = 2.025 · 10^{–2}$. Die relativen Abweichungen betragen $18.7%$ bzw. $–11%.$ Die letzte Aussage ist falsch. Erst für $x < 0.37$ gilt ${\rm Q}_{o}(x) > 1.$
(3) Für den Quotienten aus ${\rm Q}_{\rm CR}(x)$ und ${\rm Q}_{o}(x)$ gilt nach den vorgegebenen Gleichungen:
- $$q(x) = \frac{{\rm Q_{CR}}(x)}{{\rm Q_{o}}(x)} = \frac{{\rm exp}(-x^2/2)}{{\rm exp}(-x^2/2)/({\sqrt{2\pi} \cdot x})} = {\sqrt{2\pi} \cdot x}$$
- $$\Rightarrow \hspace{0.3cm} q(x) \approx 2.5 \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} q(x =2) = 5\hspace{0.05cm}, \hspace{0.2cm}q(x =4) = 10\hspace{0.05cm}, \hspace{0.2cm}q(x =6) = 15\hspace{0.05cm}.$$
Je größer der Abszissenwert x, um so ungenauer wird ${\rm Q}(x)$ durch ${\rm Q}_{\rm CR}(x)$ angenähert. Bei Betrachtung der Grafik auf der Angabenseite hat man (hatte ich) den Eindruck, dass ${\rm Q}_{\rm CR}(x)$ sich aus ${\rm Q}(x)$ durch Verschieben nach unten bzw. Verschieben nach oben ergibt. Das ist aber nur eine optische Täuschung und entspricht nicht dem Sachverhalt.
(4) Mit K = 0.5 stimmt die neue Schranke $0.5 · {\rm Q}_{\rm CR}(x)$ für $x = 0$ exakt mit ${\rm Q}(x=0) = 0.500$ überein. Für größere Abszissenwerte wird damit auch die Verfälschung $q = 1.25 · x$ nur halb so groß.