Signaldarstellung/Fouriertransformation und -rücktransformation: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
Wael (Diskussion | Beiträge) |
||
| Zeile 7: | Zeile 7: | ||
== # ÜBERBLICK ZUM DRITTEN HAUPTKAPITEL # == | == # ÜBERBLICK ZUM DRITTEN HAUPTKAPITEL # == | ||
| − | Im zweiten Kapitel wurden periodische Signale durch eine Reihe harmonischer Schwingungen („Fourierreihe”) beschrieben. Verringert man – zumindest gedanklich – die Wiederholfrequenz eines periodischen Signals immer mehr, das heißt, die Periodendauer wird immer länger, so kommt man vom periodischen Signal (<i>Puls</i>) zum einmaligen <b><font color="#cc0000">aperiodischen Signal</b></font> – häufig auch als <font color="#cc0000"><b>Impuls</b></font> bezeichnet. | + | Im zweiten Kapitel wurden periodische Signale durch eine Reihe harmonischer Schwingungen („Fourierreihe”) beschrieben. Verringert man – zumindest gedanklich – die Wiederholfrequenz eines periodischen Signals immer mehr, das heißt, die Periodendauer wird immer länger, so kommt man vom periodischen Signal (<i>Puls</i>) zum einmaligen <b> <font color="#cc0000">aperiodischen Signal</b> </font> – häufig auch als <font color="#cc0000"> <b>Impuls</b></font> bezeichnet. |
Im Folgenden werden solche aperiodischen, impulsförmigen Signale betrachtet und im Zeit– und Frequenzbereich mathematisch beschrieben. Das Kapitel beinhaltet im Einzelnen: | Im Folgenden werden solche aperiodischen, impulsförmigen Signale betrachtet und im Zeit– und Frequenzbereich mathematisch beschrieben. Das Kapitel beinhaltet im Einzelnen: | ||
Version vom 27. Dezember 2017, 14:05 Uhr
Inhaltsverzeichnis
# ÜBERBLICK ZUM DRITTEN HAUPTKAPITEL #
Im zweiten Kapitel wurden periodische Signale durch eine Reihe harmonischer Schwingungen („Fourierreihe”) beschrieben. Verringert man – zumindest gedanklich – die Wiederholfrequenz eines periodischen Signals immer mehr, das heißt, die Periodendauer wird immer länger, so kommt man vom periodischen Signal (Puls) zum einmaligen aperiodischen Signal – häufig auch als Impuls bezeichnet.
Im Folgenden werden solche aperiodischen, impulsförmigen Signale betrachtet und im Zeit– und Frequenzbereich mathematisch beschrieben. Das Kapitel beinhaltet im Einzelnen:
- die Herleitung der beiden Fourierintegrale aus der Fourierreihe,
- die Erweiterung des Fourierintegrals zur Fouriertransformation mittels Distributionen,
- einige Sonderfälle impulsartiger Signale wie Rechteck– Gauß– und Diracimpuls,
- die Gesetzmäßigkeiten der Fouriertransformation, und schließlich
- die Bedeutung der Faltungsoperation und deren vielfältige Anwendungen.
Die Laplace– und die Hilberttransformation, die ausschließlich für kausale Signale bzw. Systeme anwendbar sind, werden erst im nächsten Buch „Lineare zeitinvariante Systeme” behandelt.
Verringert man – zumindest gedanklich – die Wiederholfrequenz eines periodischen Signals immer mehr, das heißt, die Periodendauer wird immer länger, so kommt man vom periodischen Signal zum einmaligen aperiodischen Signal bezeichnet.
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Kapitel 6: Lineare zeitinvariante Systeme, Programm lzi
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms und
- dieser Praktikumsanleitung ⇒ Link verweist auf die PDF-Version; Kapitel 6: Seite 99-118.
Eigenschaften aperiodischer Signale
Im letzten Kapitel haben wir periodische Signale betrachtet. Das wesentliche Charakteristikum dieser Signale ist, dass für sie eine Periodendauer $T_0$ angegeben werden kann. Ist eine solche Periodendauer nicht angebbar oder – was in der Praxis das gleiche ist – hat $T_0$ einen unendlich großen Wert, so spricht man von einem aperiodischen Signal.
Für das vorliegende Kapitel „Aperiodische Signale - Impulse” sollen folgende Voraussetzungen gelten:
- Die betrachteten Signale $x(t)$ sind aperiodisch und energiebegrenzt, das heißt, sie besitzen nur eine endliche Energie $E_x$ und eine vernachlässigbar kleine (mittlere) Leistung $P_x$.
- Oft konzentriert sich die Energie dieser Signale auf einen relativ kurzen Zeitbereich, so dass man auch von impulsförmigen Signalen spricht.
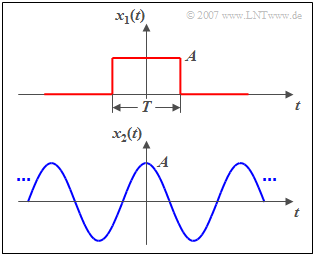
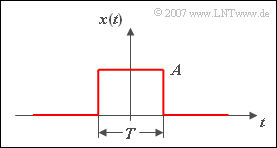
Die Grafik zeigt oben einen Rechteckimpuls $x_1(t)$ mit Amplitude $A$ und Dauer $T$ als Beispiel eines aperiodischen und zeitlich begrenzten Signals. Dieser Impuls besitzt
- eine endliche Signalenergie ($E_1=A^2 \cdot T$), und
- die Leistung $P_1$ = 0.
Ein leistungsbegrenztes Signal, zum Beispiel das unten dargestellte Cosinussignal $x_2(t)$, besitzt dagegen
- stets eine endliche Leistung ($P_2=A^2/2$), und
- eine unendlich große Signalenergie ($E_2 \to \infty$).
Genauere Betrachtung der Fourierkoeffizienten
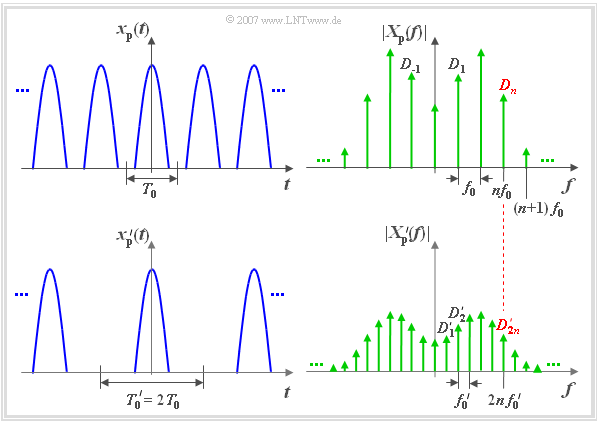
Wir gehen von einem periodischen Signal $x_{\rm P}(t)$ mit der Periodendauer $T_0$ aus, das entprechend den Ausführungen auf der Seite Komplexe Fourierreihe wie folgt dargestellt werden kann:
$$x_{\rm P}(t)=\sum^{+\infty}_{n=-\infty}D_{\it n}\cdot \rm e^{j 2 \pi \hspace{-0.05cm}{\it n} \it t / T_{\rm 0}}.$$
Die Fourierkoeffizienten sind im Allgemeinen komplex, und es gilt $D_{-n}=D_n^\ast$:
$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} \it t / T_{\rm 0}}\, {\rm d}t.$$
Die dazugehörige Spektralfunktion $X_{\rm P}(f)$ ist ein so genanntes Linienspektrum mit Spektrallinien im Abstand $f_0=1/T_0$:
$$X_{\rm P}(f)=\sum^{+\infty}_{n=-\infty}D_n\cdot\delta(f-n\cdot f_0).$$
Die obere Grafik zeigt links das periodische Zeitsignal $x_{\rm P}(t)$ und rechts das zugehörige Betragsspektrum $X_{\rm P}(f)$.
Anmerkung: Es handelt sich hierbei lediglich um eine schematische Skizze. Ist $x_{\rm P}(t)$ eine reelle und gerade Funktion, so ist $X_{\rm P}(f)$ ebenfalls reell und gerade. Die Gleichung $X_{\rm P}(f) = |X_{\rm P}(f)|$ gilt allerdings nur dann, wenn alle Spektrallinien zudem auch positiv sind.
In der unteren Grafik ist links ein weiteres periodisches Signal $x_{\rm P}'(t)$ mit doppelter Periodendauer $T_0' = 2 \cdot T_0$ dargestellt. Für dieses Signals gilt:
$${x_{\rm P}}'(t)=\sum^{+\infty}_{n=-\infty}{\it D_n}'\cdot {\rm e}^{{\rm j} 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}'} \hspace{0.3cm}{\rm mit}\hspace{0.3cm}{\it D_n}'=\frac{1}{{T_0}'}\cdot \int^{{+T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n t / T}_{\rm 0}'}\, {\rm d}\it t.$$
Im Bereich von $-T_0/2$ bis $+T_0/2$ sind die beiden Signale identisch.
Betrachten wir auch hier die Spektralfunktion $X_P'(f)$ entsprechend der rechten Skizze:
- Aufgrund der doppelten Periodendauer ($T_0' = 2 \cdot T_0$) liegen nun die Spektrallinien enger beisammen ($f_0' = f_0/2$).
- Die beiden Koeffizienten $D_n$ und ${D_{2n}}'$ – im Bild rot hervorgehoben – gehören zur gleichen physikalischen Frequenz $f = n \cdot f_0 = 2n \cdot f_0'$.
Wir erkennen durch Analyse der Koeffizienten
$$D_n=\frac{1}{T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} \it t / T_{\rm 0}}\, {\rm d}t \hspace{0.5cm}\text{und} \hspace{0.5cm} {D_{2n}}'=\frac{1}{{T_0}'}\cdot \int^{+{T_0}'/2}_{-{T_0}'/2}{x_{\rm P}}'(t) \cdot{\rm e}^{-\rm j 4 \pi \hspace{-0.05cm}{\it n} \it t / {T_{\rm 0}}'}\, {\rm d}t \text{:} $$
- Zwischen $T_0/2$ und $T_0'/2$ ist ${x_{\rm P}}'(t)$ identisch 0, ebenso im dazu symmetrischen Intervall bei negativen Zeiten.
- Deshalb können die Integrationsgrenzen auf $\pm T_0/2$ eingeschränkt werden.
- Innerhalb der neuen Integrationsgrenzen kann ${x_{\rm P}}'(t)$ durch $x_{\rm P}(t)$ ersetzt werden.
Setzen wir nun in obiger Gleichung noch $T_0' = 2T_0$, so erhalten wir:
$${D_{2n}}'=\frac{1}{2T_0}\cdot \int^{+T_0/2}_{-T_0/2}x_{\rm P}(t) \cdot{\rm e}^{-\rm j 2 \pi \hspace{-0.05cm}{\it n} t / T_{\rm 0}}\, {\rm d}t = {D_n}/{2} .$$
Fassen wir dieses Ergebnis kurz zusammen:
- Die Spektrallinie des Signals ${x_{\rm P}}'(t)$ bei der Frequenz $f = n \cdot f_0'$ wird mit ${D_{2n}}'$ bezeichnet (untere Grafik).
- Diese Linie ist genau halb so groß wie die Spektrallinie $D_n$ des Signals $x_{\rm P}(t)$ bei der gleichen physikalischen Frequenz $f$ (obere Grafik).
- Die Spektralfunktion ${X_{\rm P}}'(f)$ weist gegenüber $X_P(f)$ zusätzliche Spektrallinien bei $(n + 1/2) \cdot f_0$ auf. Diese führen dazu, dass im Zeitbereich jeder zweite Impuls von $x_{\rm P}(t)$ um $n \cdot T_0$ gelegen ($n$ ungeradzahlig) ausgelöscht wird.
Vom periodischen zum aperiodischen Signal
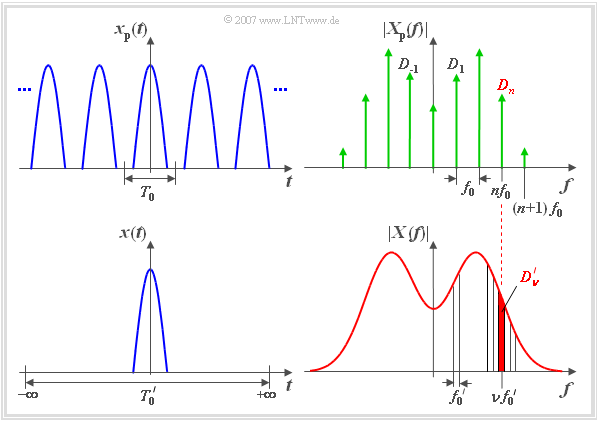
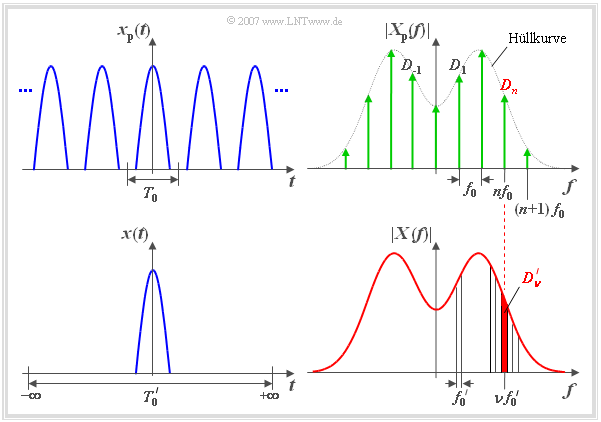
Wir greifen nun die Überlegungen der vorherigen Seite auf und wählen die Periodendauer $T_0'$ von ${x_{\rm P}}'(t)$ allgemein um einen ganzzahligen Faktor $k$ größer als die Periodendauer $T_0$ von ${x_{\rm P}}(t)$. Dann können die bisherigen Aussagen verallgemeinert werden:
- Der Linienabstand ist bei ${X_{\rm P}}'(f)$ um den Faktor $k$ geringer als beim Spektrum ${X_{\rm P}}(f)$.
- Um diesen Sachverhalt hervorzuheben, bezeichnen wir die Frequenz-Laufvariable der Funktion ${X_{\rm P}}'(f)$ mit $\nu$ anstelle von $n$. Es gilt: $\nu=k \cdot n$.
- Für die Spektrallinie des Signals ${X_{\rm P}}'(f)$ bei der Frequenz $f=n \cdot f_0 =\nu \cdot f_0'$ gilt:
$${D_\nu}' = {1}/{k} \cdot D_n, \hspace{0.5cm} {\rm wobei} \hspace{0.5cm} \nu = k \cdot n .$$
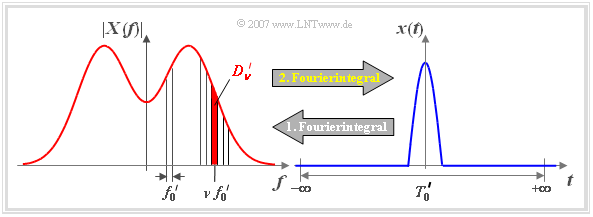
Wählt man nun – wie im Bild schematisch dargestellt – den Faktor $k$ und damit die Periodendauer $T_0'$ immer größer und lässt sie schließlich nach unendlich gehen, so
- geht das periodische Signal ${x_{\rm P}}(t)$ in das aperiodische Signal $x(t)$ über,
- kann man das Linienspektrum ${X_{\rm P}}(f)$ durch das kontinuierliche Spektrum $X(f)$ ersetzen.
Das erste Fourierintegral
Bezüglich den Spektralfunktion $X_{\rm P}(f)$ und $X(f)$ lassen sich somit folgende Aussagen machen:
- Die einzelnen Spektrallinien liegen nun beliebig eng beieinander ($f_0'=1/T_0' \to 0$).
- In der Spektralfunktion $X(f)$ treten nun innerhalb bestimmter Intervalle alle möglichen (nicht nur diskrete) Frequenzen auf. Damit stellt $X(f)$ kein Linienspektrum mehr dar.
- Der Beitrag einer jeden einzelnen Frequenz $f$ zum Signal ist nur verschwindend gering ($k \to \infty, {D_{\nu}}' \to 0$). Aufgrund der unendlich vielen Frequenzen ergibt sich jedoch insgesamt ein endliches Resultat.
- Anstatt die Fourierkoeffizienten ${D_{\nu}}'$ zu berechnen, wird nun eine spektrale Dichte $X(f)$ ermittelt. Bei der Frequenz $f=\nu\cdot f_0'$ gilt dann:
- $$X(f = {\rm \nu} {f_{\rm 0}}') = \lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm} 0} ({{D_{\rm \nu}}'}/{{f_{\rm 0}}'}) = \lim_{{T_{\rm 0}}' \to \infty} ({D_{\rm \nu}}' \cdot {T_{\rm 0}}').$$
- Die Spektralfunktion (Dichte) $X(f)$ des aperiodischen Signals $x(t)$ ist im Spektrum $X_{\rm P}(f)$ des vergleichbaren periodischen Signals $x_{\rm P}(t)$ als Einhüllende erkennbar (siehe Grafiken).
- In der unteren Grafik entspricht ${D_{\nu}}'$ der rot hinterlegten Fläche des Frequenzintervalls um $\nu \cdot f_0'$ mit der Breite $f_0'$.
Verwendet man die auf der letzten Seite angegebenen Gleichungen, so erhält man:
$$X(f = {\rm \nu} \cdot {f_{\rm 0}}') = \lim_{{T_{\rm 0}'} \to \infty} \int ^{{T_{\rm 0}}'/2} _{-{T_{\rm 0}}'/2} x_{\rm P}(t) \, \cdot \, { \rm e}^{-\rm j 2\pi\nu \it {f_{\rm 0}}' t} \,{\rm d}t.$$
Durch den gemeinsamen Grenzübergang ($T_0' \to \infty, f_0' \to 0$) wird nun
- aus dem periodischen Signal $x_{\rm P}(t)$ das aperiodische Signal $x(t)$, und
- aus der diskreten Frequenz $\nu \cdot {f_0}'$ die kontinuierliche Frequenzvariable $f$.
Damit erhält man eine fundamentale Definition, welche die Berechnung der Spektralfunktion einer aperiodischen Zeitfunktion ermöglicht. Der Name dieser Spektraltransformation geht auf den französischen Physiker Jean-Baptiste-Joseph Fourier zurück.
Die Spektralfunktion (oder kurz: das Spektrum) eines aperiodischen und gleichzeitig energiebegrenzten Signals $x(t)$ ist wie folgt zu berechnen ⇒ Erstes Fourierintegral :
$$X(f)= \hspace{0.05cm}\int_{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t$$
Das Lernvideo Unterschiede und Gemeinsamkeiten von kontinuierlichen und diskreten Spektren soll Ihnen die Aussagen der letzten Seiten nochmals verdeutlichen
Gegeben ist der skizzierte Zeitverlauf $x(t)$. Gesucht ist das zugehörige Spektrum $X(f)$. Wir wenden dazu das erste Fourierintegral an.
- Aus obiger Darstellung ist zu erkennen, dass für $|t| > T/2$ das Signal $x(t) = 0$ ist. Das bedeutet, dass das Integrationsintervall auf den Bereich $\pm T/2$ begrenzt werden kann.
- Damit erhält man den Ansatz:
$$ \begin{align*} X(f) & = A \cdot \int_{-T/2}^{+T/2} {\rm e}^{-{\rm j2\pi} ft}\,{\rm d}t = \frac{ A}{-\rm j2\pi f}\left[ {\rm e}^{-{\rm j}2\pi ft}\right]_{-T/2}^{+T/2} \\ & = \frac{\it A} {-\rm j 2\pi f}\cdot \left[\cos({\rm \pi} f T)-{\rm j} \cdot \sin({\rm \pi} fT)-\cos({\rm \pi} fT)-{\rm j} \cdot \sin({\rm \pi} fT)\right] \hspace{0.5cm}\Rightarrow \hspace{0.5cm}X(f)=A\cdot \frac{\sin({\rm \pi} fT)}{{\rm \pi} f}.\end{align*}$$
- Erweitert man Zähler und Nenner mit $T$, so erhält man:
$$X(f)=A\cdot T \cdot\frac{\sin(\pi fT)}{\pi fT} = A\cdot T \cdot{\rm si }(\pi fT) .$$
Die Funktion $\text{si}(x) = \sin(x)/x$ wird auf der späteren Seite Rechteckimpuls noch eingehend analysiert. Man nennt sie „si–Funktion” oder auch „Spaltfunktion”.
Betrachten wir noch die Einheiten der beiden Funktionen im Zeit- und Frequenzbereich:
- Ist $x(t)$ beispielsweise eine Spannung, so hat die Impulsamplitude $A$ die Einheit „Volt”.
- Die Dimension der Größe $T$ ist häufig die Zeit, z. B. mit der Einheit „Sekunde”.
- Der Kehrwert der Zeit entspricht der Frequenz mit der Einheit „Hertz”.
- Das Argument $f \cdot T$ ist dimensionslos.
- Die Spektralfunktion $X(f)$ hat somit beispielsweise die Einheit „V/Hz”.
Fouriertransformation
Das Spektrum $X(f)$ eines Signals $x(t)$ lautet gemäß dem „Ersten Fourierintegral”:
$$X(f)= \hspace{0.05cm}\int _{-\infty} ^{{+}\infty} x(t) \, \cdot \, { \rm e}^{-\rm j 2\pi \it ft} \,{\rm d}t.$$
Wie auf der letzten Seite an einem einfachen Beispiel gezeigt wurde, ist dieses Integral bei einem energiebegrenzten Signal $x(t)$ problemlos lösbar. Das Fourierintegral divergiert aber bei nicht energiebegrenzten Signalen, zum Beispiel
- einem Gleichsignal ,
- einer harmonischen Schwingung, oder (vgl. Kapitel 2.3),
- einem anklingenden Signal.
Unter Einbeziehung einer beidseitig abfallenden Hilfsfunkion $\varepsilon (t)$ kann allerdings die Konvergenz erzwungen werden:
$$X(f) = \lim_{\varepsilon \to 0} \int _{-\infty} ^{{+}\infty} x(t) \cdot {\rm e}^{\it -\varepsilon | \hspace{0.01cm} t \hspace{0.01cm} |} \cdot {\rm e}^{{-\rm j 2 \pi}\it ft} \,{\rm d}t.$$
Solche nicht energiebegrenzten Signale führen im Spektrum zu so genannten „Diracfunktionen”, manchmal auch „Distributionen” genannt.
Man bezeichnet diesen allgemeinen Funktionalzusammenhang $X(f) = F[x(t)]$ als Fouriertransformation und verwendet hierfür die Kurzschreibweise (mit dem „weißen” Punkt für den Zeitbereich und dem ausgefüllten Punkt für den Spektralbereich):
$$X(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,x(t).$$
Bei einem anklingenden Signal wird die Konvergenz allerdings nur dann erreicht, solange die Zeitfunktion weniger als exponentiell ansteigt.
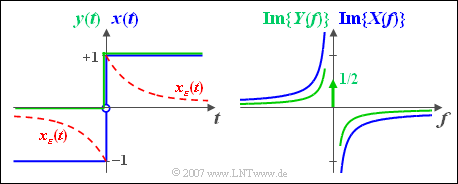
Wir betrachten eine akausale Sprungfunktion $x(t) = \text{sign}(t)$ mit $x(t)= –1$ für negative Zeiten sowie $x(t) = +1$ für positive Zeiten. Dieses Signal ist in der linken Skizze in blauer Farbe dargestellt.
Da das Signal $x(t)$ nach beiden Seiten bis ins Unendliche reicht, muss zur Berechnung der Fouriertransformierten für beide Abschnitte zunächst ein geeigneter Konvergenzfaktor $\text{e}^{-\varepsilon |t|}$ hinzugefügt werden (es gelte $\varepsilon > 0$). Die resultierende Zeitfunktion lautet dann:
$$x_\varepsilon (t) = \left\{ {\begin{array}{*{20}c} {{\rm{e}}^{ - \varepsilon t} } & {{\rm{f\ddot{u}r}}\quad t > 0,} \\ {{\rm{ - e}}^{\varepsilon t} } & {{\rm{f\ddot{u}r}}\quad t < 0.} \\\end{array}} \right.$$
Nach ähnlicher Vorgehensweise wie auf der Seite Diracfunktion im Frequenzbereich ergibt sich für die zugehörige Spektralfunktion
$$X_\varepsilon (f) = \frac{1}{{\varepsilon + {\rm{j}}2{\rm{\pi }}f}} - \frac{1}{{\varepsilon - {\rm{j}}2{\rm{\pi }}f}} = \frac{{ - {\rm{j4\pi }}f}}{{\varepsilon ^2 + \left( {2{\rm{\pi }}f} \right)^2 }}.$$
Eigentlich interessieren wir uns aber für das Spektrum der tatsächlichen Sprungfunktion. Für diese gilt:
$$x(t) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm}\to \hspace{0.05cm}0 } x_\varepsilon (t).$$
Deshalb ist auch die Spektralfunktion $X(f) =\text{F}[x(t)]$ als Grenzwert von $X_\varepsilon(f)$ für $\varepsilon \to 0$ zu bestimmen:
$$X(f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 } X_\varepsilon (f) = \frac{{ - {\rm{j}}}}{{{\rm{\pi }}f}} = \frac{1}{{{\rm{j\pi }}f}}.$$
In der rechten Grafik ist die rein imaginäre Spektralfunktion $X(f)$ als blaue Kurve dargestellt. Man erkennt, dass $|X(f)|$ mit zunehmender Frequenz kontinuierlich abnimmt.
Der grüne Kurvenzug in der linken Grafik zeigt das Signal $y(t)$, das sich von $x(t)$ nur bei den negativen Zeiten unterscheidet. In diesem Bereich gilt $y(t) = 0$. Die zugehörige Spektralfunktion $Y(f)$ ist im gesamten Bereich nur halb so groß wie $X(f)$. Dies zeigt die nachfolgende Rechnung:
$$Y(f) = \mathop {\lim }\limits_{\varepsilon \to 0 } Y_\varepsilon (f) = \mathop {\lim }\limits_{\varepsilon \hspace{0.05cm} \to \hspace{0.05cm}0 }\frac{1}{{\varepsilon + {\rm{j}}2{\rm{\pi }}f}} = \frac{1}{{{\rm{j2\pi }}f}}.$$
Zudem ergibt sich auf Grund des Gleichanteils nun noch eine Diracfunktion bei $f = 0$ mit dem Gewicht $1/2$. Hierauf wird im Beispiel zum Abschnitt Zuordnungssatz noch im Detail eingegangen.
Das zweite Fourierintegral
Bisher wurde lediglich gezeigt, wie man für ein aperiodisches, impulsförmiges Signal $x(t)$ die zugehörige Spektralfunktion $X(f)$ berechnet. Nun wenden wir uns der umgekehrten Aufgabe zu, nämlich: Wie ermittelt man die Zeitfunktion $x(t)$ aus der Spektralfunktion $X(f)$?
Mit den gleichen Bezeichnungen wie auf den ersten Seiten dieses Kapitels kann man das Signal $x(t)$ als Fourierreihe schreiben, wobei nun der Grenzübergang $f_0' \to 0$ zu berücksichtigen ist:
$$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty}{D_{\it \nu}}' \cdot \rm e^{j 2 \pi \it\nu {f_{\rm 0}}' t}.$$
Erweitert man nun sowohl den Zähler als auch den Nenner um ${f_0}'$, so erhält man:
$$x(t)=\lim_{{f_{\rm 0}}' \hspace{0.05cm}\to \hspace{0.05cm}0} \sum^{+\infty}_{\nu = -\infty} ({{D_{\it \nu}}'}/{{f_{\rm 0}}'}) \cdot \rm e^{j 2 \pi \it \nu {f_{\rm 0}}' t} \cdot {\it f_{\rm 0}}'.$$
Der Grenzübergang ${f_0}' \to 0$ hat nun folgende Auswirkungen:
- Die (unendliche) Summe wird zu einem Integral, wobei ${f_0}'$ formal durch die differenzielle Größe $\text{d}f$ (Integrationsvariable) zu ersetzen ist.
- Die Größe $\nu \cdot{f_0}'$ im Exponenten beschreibt die physikalische Frequenz $f$.
- Der Quotient ${D_{\nu}}'/{f_0}'$ ergibt die Spektralfunktion $X(f)$ bei der Frequenz $f$.
Unter Berücksichtigung dieser Eigenschaften kommt man zum zweiten Fourierintegral.
Ist die Spektralfunktion $X(f)$ eines aperiodischen und energiebegrenzten Signals gegeben, so lautet die dazugehörige Zeitfunktion ⇒ Zweites Fourierintegral :
$$x(t) = \hspace{0.01cm}\int_{-\infty} ^{{+}\infty} X(f) \, \cdot \, { \rm e}^{\rm j 2\pi \it ft} \,{\rm d}f.$$
Aufgaben zum Kapitel
Aufgabe 3.1: Spektrum des Exponentialimpulses
Zusatzaufgabe 3.1Z: Spektrum des Dreieckimpulses
Aufgabe 3.2: Vom Spektrum zum Signal
Zusatzaufgabe 3.2Z: si^2-Spektrum mit Diracs