Aufgaben:Aufgabe 1.8: Variable Flankensteilheit

• Zurück zum Buch

Trapez–Tiefpass und Cosinus–Rolloff–Tiefpass

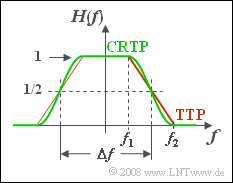
Zwei Tiefpässe mit variabler Flankensteilheit sollen miteinander verglichen werden. Für Frequenzen $|f| ≤ f_1$ gilt in beiden Fällen $H(f) = 1$. Dagegen werden alle Frequenzen $|f| ≥ f_2$ vollständig unterdrückt.

Im mittleren Bereich $f_1 ≤ |f| ≤ f_2$ sind die Frequenzgänge durch folgende Gleichungen festgelegt:

• Trapeztiefpass (TTP):

$$H(f) = \frac{f_2 - |f|}{f_2 - f_1} ,$$

• Cosinus–Rolloff–Tiefpass (CRTP):

$$H(f) = \cos^2 \left(\frac{|f|- f_1}{f_2 - f_1} \cdot\frac{\pi}{2} \right).$$

Alternative Systemparameter sind für beide Tiefpässe

• die über das flächengleiche Rechteck definierte äquivalente Bandbreite $Δf$, sowie
• der Rolloff–Faktor (im Frequenzbereich):

$$r=\frac{f_2 - f_1}{f_2 + f_1} .$$

In der gesamten Aufgabe gelte $Δf = 10 \ \rm kHz$ und $r = 0.2$. Die Impulsantworten lauten mit der äquivalenten Impulsdauer $Δt = 1/Δf = 0.1 \ \rm ms$:

$$h_{\rm TTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot \frac{t}{\Delta t} )\cdot {\rm si}(\pi \cdot r \cdot \frac{t}{\Delta t} ),$$

$$h_{\rm CRTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot \frac{t}{\Delta t} )\cdot \frac {\cos(\pi \cdot r \cdot t / \Delta t )}{1 - (2 \cdot r \cdot t/\Delta t )^2}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Einige systemtheoretische Tiefpassfunktionen.
• Bezug genommen wird insbesondere auf die Seiten Trapez–Tiefpass sowie Cosinus–Rolloff–Tiefpass.
• Sie können Ihre Ergebnisse mit dem interaktiven Applet Frequenzgang und Impulsantwort überprüfen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Wie lautet die Gleichung für die äquivalente Bandbreite $Δf$? Es gilt

	$Δf = f_2 - f_1$,
	$Δf = f_1 + f_2$,
	$Δf = (f_2 + f_1)/2$.

2

Bestimmen Sie die Tiefpass-Parameter $f_1$ und $f_2$ für $Δf = 10 \ \rm kHz$ und $r = 0.2$.

$f_1 \ = \ $ $\ \rm kHz$

$f_2 \ = \ $ $\ \rm kHz$

3

Welche Aussagen sind für die Impulsantwort des Trapez–Tiefpasses zutreffend, wenn $r = 0.2$ vorausgesetzt wird?

	$h(t)$ besitzt Nullstellen bei $±n · Δt (n = 1, 2, \text{...})$.
	$h(t)$ besitzt zusätzliche Nullstellen zu anderen Zeiten.
	Mit $r = 0$ würde $h(t)$ schneller abklingen.
	Mit $r = 1$ würde $h(t)$ schneller abklingen.

4

Welche Aussagen treffen für die Impulantwort des Cosinus–Rolloff–Tiefpasses zu, wenn $r = 0.2$ vorausgesetzt wird?

	$h(t)$ besitzt Nullstellen bei $±n · Δt (n = 1, 2, \text{...})$.
	$h(t)$ besitzt zusätzliche Nullstellen zu anderen Zeiten.
	Mit $r = 0$ würde $h(t)$ schneller abklingen.
	Mit $r = 1$ würde $h(t)$ schneller abklingen.

Musterlösung

Musterlösung

(1)  Bei beiden Tiefpässen ist das Integral über H(f) gleich f₁ + f₂. Wegen H(f = 0) = 1 gilt somit der Lösungsvorschlag 2:   $\Delta f = f_1 + f_2.$

(2)  Setzt man die unter (1) gefundene Beziehung in die Definitionsgleichung des Rolloff–Faktors ein, so erhält man $${f_2 - f_1} = r \cdot \Delta f = {2\,\rm kHz}, \hspace{0.5cm} {f_2 + f_1} = {10\,\rm kHz}.$$

Durch Addition bzw. Subtraktion beider Gleichungen ergeben sich die so genannten „Eckfrequenzen” zu $f_1 \underline{= 4 \ \rm kHz}$ und $f_2 \underline{= 6 \ \rm kHz}$.

(3)  Richtig sind die Lösungsvorschläge 1 und 4:

• Die erste si–Funktion von h_TTP(t) führt zu Nullstellen im Abstand Δt (siehe auch Gleichung auf der Angabenseite).
• Die zweite si–Funktion bewirkt Nullstellen bei Vielfachen von 5 · Δt. Da diese exakt mit den Nullstellen der ersten si–Funktion zusammenfallen, gibt es keine zusätzlichen Nullstellen.
• Der Sonderfall $r = 0$ entspricht dem idealen rechteckförmigen Tiefpass mit si–förmiger Impulsantwort. Diese klingt extrem langsam ab.
• Dagegen fällt die si²–förmige Impulsantwort des Dreiecktiefpasses (Sonderfall für $r = 1$) asymptotisch mit $1/t^2$ und damit schneller als mit $r = 0.2$.

(4)  Richtig sind hier die Vorschläge 1, 2 und 4:

• Die Impulsantwort $h_{CRTP}(t)$ des Cosinus-Rolloff-Tiefpasses weist aufgrund der si–Funktion ebenfalls Nullstellen im Abstand $\Delta t$ auf.
• Die Cosinusfunktion hat Nullstellen zu folgenden Zeitpunkten:

$${\cos(\pi \cdot r \cdot {t}/{ \Delta t} )} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}r \cdot {t}/{ \Delta t} = \pm 0.5, \pm 1.5, \pm 2.5, ... \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm 2.5, \pm 7.5, \pm 12.5, ... $$

$$\Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm 2.5, \pm 7.5, \pm 12.5, ... $$

• Die Nullstelle des Zählers bei $t / \Delta t = 2.5$ wird allerdings durch den ebenfalls verschwindenden Nenner zunichte gemacht. Die weiteren Nullstellen bei $7.5, 12.5, ... $ bleiben dagegen bestehen.
• Auch hier führt $r = 0$ zum Rechtecktiefpass und damit zur si–förmigen Impulsantwort. Dagegen klingt die Impulsantwort des Cosinus–Quadrat–Tiefpasses (Sonderfall für $r = 1$) extrem schnell ab. Dieser wird in der Zusatzaufgabe 1.8Z eingehend untersucht.