Applets:Binomial- und Poissonverteilung (Applet): Unterschied zwischen den Versionen
Jimmy (Diskussion | Beiträge) |
|||
| Zeile 22: | Zeile 22: | ||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
<br> | <br> | ||
| − | === | + | ===Eigenschaften der Binomialverteilung=== |
<br> | <br> | ||
| − | Die | + | Die ''Binomialverteilung'' stellt einen wichtigen Sonderfall für die Auftrittswahrscheinlichkeiten einer diskreten Zufallsgröße dar. Zur Herleitung gehen wir davon aus, dass $I$ binäre und statistisch voneinander unabhängige Zufallsgrößen $b_i \in \{0, 1 \}$ |
| − | $$ | + | *den Wert $1$ mit der Wahrscheinlichkeit ${\rm Pr}(b_i = 1) = p$, und |
| + | *den Wert $0$ mit der Wahrscheinlichkeit ${\rm Pr}(b_i = 0) = 1-p$ annehmen kann. | ||
| − | |||
| − | + | Dann ist die Summe $z$ ebenfalls eine diskrete Zufallsgröße mit dem Symbolvorrat $\{0, 1, 2, \text{...}\ , I\}$, die man als binomialverteilt bezeichnet: | |
| + | :$$z=\sum_{i=1}^{I}b_i.$$ | ||
| + | Der Symbolumfang beträgt somit $M = I + 1.$ | ||
| − | + | '''Wahrscheinlichkeiten der Binomialverteilung''' | |
| + | |||
| + | Hierfür gilt mit $μ = 0, \text{...}\ , I$: | ||
| + | :$$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$ | ||
| + | Der erste Term gibt hierbei die Anzahl der Kombinationen $(I \text{ über }\mu)$ an: | ||
| + | :$${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$ | ||
| − | + | '''Momente der Binomialverteilung''' | |
| + | Für das Moment $k$-ter Ordnung einer binomialverteilten Zufallsgröße gilt: | ||
| + | :$$m_k={\rm E}[z^k]=\sum_{\mu={\rm 0}}^{I}\mu^k\cdot{I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$ | ||
| − | *$ | + | Daraus erhält man nach einigen Umformungen für |
| + | *den linearen Mittelwert: $m_1 = I\cdot p,$ | ||
| + | *den quadratischen Mittelwert: $m_2 = (I^2-I)\cdot p^2+I\cdot p,$ | ||
| + | *die Varianz bzw. die Streuung: $\sigma^2 = {m_2-m_1^2} = {I \cdot p\cdot (1-p)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | \sigma = \sqrt{I \cdot p\cdot (1-p)}.$ | ||
| − | + | '''Anwendung der Binomialverteilung''' | |
| − | |||
| − | + | Die Binomialverteilung findet in der Nachrichtentechnik ebenso wie in anderen Disziplinen mannigfaltige Anwendungen: | |
| − | + | *Sie beschreibt die Verteilung von Ausschussstücken in der statistischen Qualitätskontrolle. | |
| + | *Auch die per Simulation gewonnene Bitfehlerquote eines digitalen Übertragungssystems ist eigentlich eine binomialverteilte Zufallsgröße. | ||
| + | *Die Binomialverteilung erlaubt die Berechnung der Restfehlerwahrscheinlichkeit bei blockweiser Codierung, wie das folgende Beispiel zeigt. | ||
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | $ | + | $\text{Beispiel 1:}$ |
| + | Überträgt man jeweils Blöcke von $I =5$ Binärsymbolen über einen Kanal, der | ||
| + | *mit der Wahrscheinlichkeit $p = 0.1$ ein Symbol verfälscht ⇒ Zufallsgröße $e_i = 1$, und | ||
| + | *entsprechend mit der Wahrscheinlichkeit $1 - p = 0.9$ das Symbol unverfälscht überträgt ⇒ Zufallsgröße $e_i = 0$, | ||
| + | |||
| − | + | so gilt für die neue Zufallsgröße $f$ („Fehler pro Block”): | |
| − | $$ | + | :$$f=\sum_{i=1}^{I}e_i.$$ |
| − | $${ | ||
| − | |||
| − | |||
| + | Die Zufallsgröße $f$ kann nun alle ganzzahligen Werte zwischen $\mu = 0$ (kein Symbol verfälscht) und $\mu = I$ (alle fünf Symbole falsch) annehmen. Die Wahrscheinlichkeiten für $\mu$ Verfälschungen bezeichnen wir mit $p_μ = {\rm Pr}(f = \mu)$. | ||
| + | *Der Fall, dass alle fünf Symbole richtig übertragen werden, tritt mit der Wahrscheinlichkeit $p_0 = 0.9^{5} ≈ 0.5905$ ein. Dies ergibt sich auch aus der Binomialformel für $μ = 0$ unter Berücksichtigung der Definition „10 über 0“ = 1. | ||
| + | *Ein einziger Symbolfehler $(f = 1)$ tritt mit der Wahrscheinlichkeit $p_1 = 5\cdot 0.1\cdot 0.9^4\approx 0.3281$ auf. Der erste Faktor berücksichtigt, dass es für die Position eines einzigen Fehlers genau $5\text{ über } 1 = 5$ Möglichkeiten gibt. Die beiden weiteren Faktoren beücksichtigen, dass ein Symbol verfälscht und vier richtig übertragen werden müssen, wenn $f =1$ gelten soll. | ||
| + | *Für $f =2$ gibt es mehr Kombinationen, nämlich$5\text{ über } 2 = (5 \cdot 4)/(1 \cdot 2) = 10$, und man erhält $p_2 = 10\cdot 0.1^2\cdot 0.9^3\approx 0.0729$. | ||
| − | + | Kann ein Blockcode bis zu zwei Fehlern korrigieren, so ist die Restfehlerwahrscheinlichkeit $p_{\rm R} = 1-p_{\rm 0}-p_{\rm 1}-p_{\rm 2}\approx 0.85\%$. Eine zweite Berechnungsmöglichkeit wäre $p_{\rm R} = p_{3} + p_{4} + p_{5}$ mit der Näherung $p_{\rm R} \approx p_{3} = 0.81\%.$ | |
| − | |||
| − | |||
| − | |||
| − | $\ | ||
| − | |||
| − | |||
| − | |||
| − | + | Die mittlere Fehleranzahl in einem Block ist $m_f = 5 \cdot 0.1 = 0.5$. Die Varianz der Zufallsgröße $f$ beträgt $\sigma_f^2 = 5 \cdot 0.1 \cdot 0.9= 0.45$ ⇒ $\sigma_f \approx 0.671.$}} | |
| − | |||
| − | |||
| − | === | + | ===Eigenschaften der Poissonverteilung=== |
<br> | <br> | ||
| − | + | Die ''Poissonverteilung'' ist ein Grenzfall der Binomialverteilung, wobei | |
| − | + | *zum einen von den Grenzübergängen $I → ∞$ und $p →$ 0 ausgegangen wird, | |
| − | + | *zusätzlich vorausgesetzt ist, dass das Produkt $I · p = λ$ einen endlichen Wert besitzt. | |
| − | * | ||
| − | |||
| − | |||
| − | + | Der Parameter $λ$ gibt die mittlere Anzahl der „Einsen” in einer festgelegten Zeiteinheit an und wird als die '''Rate''' bezeichnet. | |
| − | |||
| − | + | Im Gegensatz zur Binomialverteilung ($0 ≤ μ ≤ I$) kann hier die Zufallsgröße beliebig große (ganzzahlige, nichtnegative) Werte annehmen, was bedeutet, dass die Menge der möglichen Werte hier nicht abzählbar ist. Da jedoch keine Zwischenwerte auftreten können, spricht man auch hier von einer ''diskreten Verteilung''. | |
| − | |||
| − | |||
| − | + | '''Wahrscheinlichkeiten der Poissonverteilung''' | |
| − | |||
| − | |||
| − | |||
| − | + | Berücksichtigt man die oben genannten Grenzübergänge in der Gleichung für die Wahrscheinlichkeiten der Binomialverteilung, so folgt für die Auftrittswahrscheinlichkeiten der poissonverteilten Zufallsgröße $z$: | |
| + | :$$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$ | ||
| + | Daraus erhält man nach einigen algebraischen Umformungen: | ||
| + | :$$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$ | ||
| − | |||
| − | |||
| − | + | '''Momente der Poissonverteilung''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Bei der Poissonverteilung ergeben sich Mittelwert und Streuung direkt aus den entsprechenden Gleichungen der Binomialverteilung durch zweifache Grenzwertbildung: | Bei der Poissonverteilung ergeben sich Mittelwert und Streuung direkt aus den entsprechenden Gleichungen der Binomialverteilung durch zweifache Grenzwertbildung: | ||
:$$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} I \cdot p= \lambda,$$ | :$$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} I \cdot p= \lambda,$$ | ||
:$$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$ | :$$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$ | ||
| + | |||
| + | Daraus ist zu erkennen, dass bei der Poissonverteilung stets $\sigma^2 = m_1 = \lambda$ ist. Dagegen gilt bei der Binomialverteilung immer $\sigma^2 < m_1$. | ||
| + | |||
| + | [[Datei: P_ID616__Sto_T_2_4_S2neu.png |frame| Momente der Poissonverteilung | rechts]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 2:}$ | ||
| + | Wir vergleichen nun | ||
| + | *die Binomialverteilung mit den Parametern $I =6$ und $p = 0.4$, und | ||
| + | *die Poissonverteilung mit $λ = 2.4$: | ||
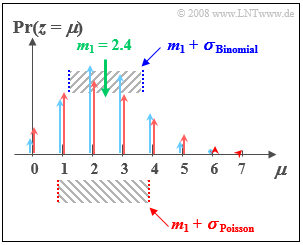
| + | *Beide Verteilungen besitzen genau den gleichen Mittelwert $m_1 = 2.4$. | ||
| + | *Bei der Poissonverteilung (im Bild rot markiert) beträgt die Streuung $σ ≈ 1.55$. | ||
| + | *Bei der (blauen) Binomialverteilung ist die Standardabweichung nur $σ = 1.2$.}} | ||
===Gegenüberstellung Binomialverteilung vs Poissonverteilung=== | ===Gegenüberstellung Binomialverteilung vs Poissonverteilung=== | ||
<br> | <br> | ||
| + | ''Weitere Hinweise:'' | ||
| + | *Für sehr große Werte von $I$ kann die Binomialverteilung durch die im nächsten Abschnitt beschriebene [[Stochastische_Signaltheorie/Poissonverteilung|Poissonverteilung]] angenähert werden. | ||
| + | *Ist gleichzeitig das Produkt $I · p \gg 1$, so geht nach dem [https://de.wikipedia.org/wiki/Satz_von_Moivre-Laplace Grenzwertsatz von de Moivre-Laplace] die Poissonverteilung (und damit auch die Binomialverteilung) in eine diskrete [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgröße|Gaußverteilung]] über. | ||
| + | |||
| + | |||
==Versuchsdurchführung== | ==Versuchsdurchführung== | ||
| Zeile 130: | Zeile 141: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(1)''' Setzen Sie Blau: Binomialverteilung $(I=5, p=0.4)$ und Rot: Binomialverteilung $(I=10, p=0.2)$. | + | '''(1)''' Setzen Sie '''Blau''': Binomialverteilung $(I=5, \ p=0.4)$ und '''Rot''': Binomialverteilung $(I=10, \ p=0.2)$. |
| − | :Wie lauten die Wahrscheinlichkeiten ${rm Pr}(z=0)$ und ${\rm Pr}(z=1)$?}} | + | :Wie lauten die Wahrscheinlichkeiten ${\rm Pr}(z=0)$ und ${\rm Pr}(z=1)$?}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Blau: }{\rm Pr}(z=0)=0.6^5=7.78\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.4 \cdot 0.6^4=25.92\%$ | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Blau: }{\rm Pr}(z=0)=0.6^5=7.78\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.4 \cdot 0.6^4=25.92\%;$ |
| − | $\hspace{1.85cm}\text{Rot: }{\rm Pr}(z=0)=0.8^10=10.74\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.2 \cdot 0.8^9=26.84\%$ | + | $\hspace{1.85cm}\text{Rot: }{\rm Pr}(z=0)=0.8^10=10.74\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.2 \cdot 0.8^9=26.84\%.$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(2)''' Es gelten die Einstellungen von (1). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(3 \le z \le 5)$?}} | + | '''(2)''' Es gelten weiter die Einstellungen von '''(1)'''. Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(3 \le z \le 5)$?}} |
| − | |||
| − | |||
| − | $\hspace{3 | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Es gilt }{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z=3) + {\rm Pr}(z=4) + {\rm Pr}(z=5)\text{, oder } |
| + | {\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$ | ||
| − | $\hspace{1.85cm}\text{Blau: }{\rm Pr}(3 \le z \le 5) = 1 - 0.6826 = 0.3174$ | + | $\hspace{1.85cm}\text{Blau: }{\rm Pr}(3 \le z \le 5) = 0.2304+ 0.0768 + 0.0102 =1 - 0.6826 = 0.3174;$ |
| − | $\hspace{1.85cm}\text{Rot: }{\rm Pr}(3 \le z \le 5) = 0.9936 - 0.6778 = 0.3158$ | + | $\hspace{1.85cm}\text{Rot: }{\rm Pr}(3 \le z \le 5) = 0.2013 + 0.0881 + 0.0264 = 0.9936 - 0.6778 = 0.3158$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(3)''' Es gelten die Einstellungen von (1). Wie unterscheiden sich Mittelwert $m_1$ und Streuung $\sigma$?}} | + | '''(3)''' Es gelten weiter die Einstellungen von '''(1)'''. Wie unterscheiden sich der Mittelwert $m_1$ und die Streuung $\sigma$ der beiden Binomialverteilungen?}} |
| − | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Mittelwert: } | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Mittelwert:}\hspace{0.2cm}m_\text{1} = I \cdot p\hspace{0.3cm} \Rightarrow\hspace{0.3cm} m_\text{1, Blau} = 5 \cdot 0.4\underline{ = 2 =} \ m_\text{1, Rot} = 10 \cdot 0.2; $ |
| − | $\hspace{1.85cm}\text{Streuung: }\sigma = m_1 | + | $\hspace{1.85cm}\text{Streuung:}\hspace{0.4cm}\sigma = \sqrt{I \cdot p \cdot (1-p)} = \sqrt{m_1 \cdot (1-p)}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_{\rm Blau} = \sqrt{2 \cdot 0.6} =1.095 \le \sigma_{\rm Rot} = \sqrt{2 \cdot 0.8} = 1.265.$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(4)''' Setzen Sie '''Blau''': Binomialverteilung $(I=15, p=0.3)$ und '''Rot''': Poissonverteilung $(\lambda=4.5)$. |
| − | :Welche Unterschiede ergeben sich | + | :Welche Unterschiede ergeben sich zwischen beiden Verteilungen hinsichtlich Mittelwert $m_1$ und Varianz $\sigma^2$?}} |
| − | |||
| − | |||
| − | $\hspace{1. | + | $\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Beide Verteilungern haben gleichen Mittelwert:}\hspace{0.2cm}m_\text{1, Blau} = I \cdot p\ = 15 \cdot 0.3\underline{ = 4.5 =} \ m_\text{1, Rot} = \lambda$; |
| − | $\hspace{1.85cm} \text{ | + | $\hspace{1.85cm} \text{Binomialverteilung: }\hspace{0.2cm} \sigma_\text{Blau}^2 = m_\text{1, Blau} \cdot (1-p)\hspace{0.15cm}\underline { = 3.15} \le \text{Poissonverteilung: }\hspace{0.2cm} \sigma_\text{Rot}^2 = \lambda\hspace{0.15cm}\underline { = 4.5}$; |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| Zeile 176: | Zeile 184: | ||
$\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0\hspace{0.5cm}\text{Näherung: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \le {\rm Pr}(z = 16) = \lambda^{16}/16!$ | $\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0\hspace{0.5cm}\text{Näherung: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \le {\rm Pr}(z = 16) = \lambda^{16}/16!$ | ||
| + | |||
| + | Die maximale Varianz $σ^2 = I/4$ ergibt sich für die charakteristische Wahrscheinlichkeit $p = 1/2$. In diesem Fall sind die Wahrscheinlichkeit symmetrisch um den Mittelwert $m_1 = I/2 \ ⇒ \ p_μ = p_{I–μ}$. | ||
| + | |||
| + | Je mehr die charakteristische Wahrscheinlichkeit $p$ vom Wert $1/2$ abweicht, | ||
| + | *um so kleiner ist die Streuung $σ$, und | ||
| + | *um so unsymmetrischer werden die Wahrscheinlichkeiten um den Mittelwert $m_1 = I · p$. | ||
Version vom 20. Februar 2018, 18:07 Uhr
Inhaltsverzeichnis
Programmbeschreibung
Dieses Applet ermöglicht die Berechnung und graphische Darstellung von Wahrscheinlichkeiten von
- Binomialverteilungen:
$$\hspace{1.5cm}p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu},$$
$\hspace{0.7cm}$wobei $I$ die Anzahl der binären und statisch voneinander unabhängigen Zufallsgrößen $b_i$ und
$\hspace{0.7cm}p={\rm Pr}(b_i=1)$ die Erfolgswahrscheinlichkeit darstellt, und
- Poissonverteilungen:
$$\hspace{1.5cm}p_\mu = {\rm Pr}(z=\mu)=\frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda},$$
$\hspace{0.7cm}$wobei die Rate$\lambda$ aus $\lambda=I\cdot p$ berechnet werden kann.
Da gleichzeitig bis zu zwei Verteilungsfunktionen eingestellt werden können, können Binomial- und Poissonverteilungen einfach miteinander verglichen werden.
Theoretischer Hintergrund
Eigenschaften der Binomialverteilung
Die Binomialverteilung stellt einen wichtigen Sonderfall für die Auftrittswahrscheinlichkeiten einer diskreten Zufallsgröße dar. Zur Herleitung gehen wir davon aus, dass $I$ binäre und statistisch voneinander unabhängige Zufallsgrößen $b_i \in \{0, 1 \}$
- den Wert $1$ mit der Wahrscheinlichkeit ${\rm Pr}(b_i = 1) = p$, und
- den Wert $0$ mit der Wahrscheinlichkeit ${\rm Pr}(b_i = 0) = 1-p$ annehmen kann.
Dann ist die Summe $z$ ebenfalls eine diskrete Zufallsgröße mit dem Symbolvorrat $\{0, 1, 2, \text{...}\ , I\}$, die man als binomialverteilt bezeichnet:
- $$z=\sum_{i=1}^{I}b_i.$$
Der Symbolumfang beträgt somit $M = I + 1.$
Wahrscheinlichkeiten der Binomialverteilung
Hierfür gilt mit $μ = 0, \text{...}\ , I$:
- $$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$
Der erste Term gibt hierbei die Anzahl der Kombinationen $(I \text{ über }\mu)$ an:
- $${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$
Momente der Binomialverteilung
Für das Moment $k$-ter Ordnung einer binomialverteilten Zufallsgröße gilt:
- $$m_k={\rm E}[z^k]=\sum_{\mu={\rm 0}}^{I}\mu^k\cdot{I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$
Daraus erhält man nach einigen Umformungen für
- den linearen Mittelwert: $m_1 = I\cdot p,$
- den quadratischen Mittelwert: $m_2 = (I^2-I)\cdot p^2+I\cdot p,$
- die Varianz bzw. die Streuung: $\sigma^2 = {m_2-m_1^2} = {I \cdot p\cdot (1-p)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma = \sqrt{I \cdot p\cdot (1-p)}.$
Anwendung der Binomialverteilung
Die Binomialverteilung findet in der Nachrichtentechnik ebenso wie in anderen Disziplinen mannigfaltige Anwendungen:
- Sie beschreibt die Verteilung von Ausschussstücken in der statistischen Qualitätskontrolle.
- Auch die per Simulation gewonnene Bitfehlerquote eines digitalen Übertragungssystems ist eigentlich eine binomialverteilte Zufallsgröße.
- Die Binomialverteilung erlaubt die Berechnung der Restfehlerwahrscheinlichkeit bei blockweiser Codierung, wie das folgende Beispiel zeigt.
$\text{Beispiel 1:}$ Überträgt man jeweils Blöcke von $I =5$ Binärsymbolen über einen Kanal, der
- mit der Wahrscheinlichkeit $p = 0.1$ ein Symbol verfälscht ⇒ Zufallsgröße $e_i = 1$, und
- entsprechend mit der Wahrscheinlichkeit $1 - p = 0.9$ das Symbol unverfälscht überträgt ⇒ Zufallsgröße $e_i = 0$,
so gilt für die neue Zufallsgröße $f$ („Fehler pro Block”):
- $$f=\sum_{i=1}^{I}e_i.$$
Die Zufallsgröße $f$ kann nun alle ganzzahligen Werte zwischen $\mu = 0$ (kein Symbol verfälscht) und $\mu = I$ (alle fünf Symbole falsch) annehmen. Die Wahrscheinlichkeiten für $\mu$ Verfälschungen bezeichnen wir mit $p_μ = {\rm Pr}(f = \mu)$.
- Der Fall, dass alle fünf Symbole richtig übertragen werden, tritt mit der Wahrscheinlichkeit $p_0 = 0.9^{5} ≈ 0.5905$ ein. Dies ergibt sich auch aus der Binomialformel für $μ = 0$ unter Berücksichtigung der Definition „10 über 0“ = 1.
- Ein einziger Symbolfehler $(f = 1)$ tritt mit der Wahrscheinlichkeit $p_1 = 5\cdot 0.1\cdot 0.9^4\approx 0.3281$ auf. Der erste Faktor berücksichtigt, dass es für die Position eines einzigen Fehlers genau $5\text{ über } 1 = 5$ Möglichkeiten gibt. Die beiden weiteren Faktoren beücksichtigen, dass ein Symbol verfälscht und vier richtig übertragen werden müssen, wenn $f =1$ gelten soll.
- Für $f =2$ gibt es mehr Kombinationen, nämlich$5\text{ über } 2 = (5 \cdot 4)/(1 \cdot 2) = 10$, und man erhält $p_2 = 10\cdot 0.1^2\cdot 0.9^3\approx 0.0729$.
Kann ein Blockcode bis zu zwei Fehlern korrigieren, so ist die Restfehlerwahrscheinlichkeit $p_{\rm R} = 1-p_{\rm 0}-p_{\rm 1}-p_{\rm 2}\approx 0.85\%$. Eine zweite Berechnungsmöglichkeit wäre $p_{\rm R} = p_{3} + p_{4} + p_{5}$ mit der Näherung $p_{\rm R} \approx p_{3} = 0.81\%.$
Die mittlere Fehleranzahl in einem Block ist $m_f = 5 \cdot 0.1 = 0.5$. Die Varianz der Zufallsgröße $f$ beträgt $\sigma_f^2 = 5 \cdot 0.1 \cdot 0.9= 0.45$ ⇒ $\sigma_f \approx 0.671.$
Eigenschaften der Poissonverteilung
Die Poissonverteilung ist ein Grenzfall der Binomialverteilung, wobei
- zum einen von den Grenzübergängen $I → ∞$ und $p →$ 0 ausgegangen wird,
- zusätzlich vorausgesetzt ist, dass das Produkt $I · p = λ$ einen endlichen Wert besitzt.
Der Parameter $λ$ gibt die mittlere Anzahl der „Einsen” in einer festgelegten Zeiteinheit an und wird als die Rate bezeichnet.
Im Gegensatz zur Binomialverteilung ($0 ≤ μ ≤ I$) kann hier die Zufallsgröße beliebig große (ganzzahlige, nichtnegative) Werte annehmen, was bedeutet, dass die Menge der möglichen Werte hier nicht abzählbar ist. Da jedoch keine Zwischenwerte auftreten können, spricht man auch hier von einer diskreten Verteilung.
Wahrscheinlichkeiten der Poissonverteilung
Berücksichtigt man die oben genannten Grenzübergänge in der Gleichung für die Wahrscheinlichkeiten der Binomialverteilung, so folgt für die Auftrittswahrscheinlichkeiten der poissonverteilten Zufallsgröße $z$:
- $$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$
Daraus erhält man nach einigen algebraischen Umformungen:
- $$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$
Momente der Poissonverteilung
Bei der Poissonverteilung ergeben sich Mittelwert und Streuung direkt aus den entsprechenden Gleichungen der Binomialverteilung durch zweifache Grenzwertbildung:
- $$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} I \cdot p= \lambda,$$
- $$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$
Daraus ist zu erkennen, dass bei der Poissonverteilung stets $\sigma^2 = m_1 = \lambda$ ist. Dagegen gilt bei der Binomialverteilung immer $\sigma^2 < m_1$.
$\text{Beispiel 2:}$ Wir vergleichen nun
- die Binomialverteilung mit den Parametern $I =6$ und $p = 0.4$, und
- die Poissonverteilung mit $λ = 2.4$:
- Beide Verteilungen besitzen genau den gleichen Mittelwert $m_1 = 2.4$.
- Bei der Poissonverteilung (im Bild rot markiert) beträgt die Streuung $σ ≈ 1.55$.
- Bei der (blauen) Binomialverteilung ist die Standardabweichung nur $σ = 1.2$.
Gegenüberstellung Binomialverteilung vs Poissonverteilung
Weitere Hinweise:
- Für sehr große Werte von $I$ kann die Binomialverteilung durch die im nächsten Abschnitt beschriebene Poissonverteilung angenähert werden.
- Ist gleichzeitig das Produkt $I · p \gg 1$, so geht nach dem Grenzwertsatz von de Moivre-Laplace die Poissonverteilung (und damit auch die Binomialverteilung) in eine diskrete Gaußverteilung über.
Versuchsdurchführung
In der folgenden Beschreibung bedeutet
- Blau: Verteilungsfunktion 1 (im Applet blau markiert)
- Rot: Verteilungsfunktion 2 (im Applet rot markiert)
(1) Setzen Sie Blau: Binomialverteilung $(I=5, \ p=0.4)$ und Rot: Binomialverteilung $(I=10, \ p=0.2)$.
- Wie lauten die Wahrscheinlichkeiten ${\rm Pr}(z=0)$ und ${\rm Pr}(z=1)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Blau: }{\rm Pr}(z=0)=0.6^5=7.78\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.4 \cdot 0.6^4=25.92\%;$
$\hspace{1.85cm}\text{Rot: }{\rm Pr}(z=0)=0.8^10=10.74\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.2 \cdot 0.8^9=26.84\%.$
(2) Es gelten weiter die Einstellungen von (1). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(3 \le z \le 5)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Es gilt }{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z=3) + {\rm Pr}(z=4) + {\rm Pr}(z=5)\text{, oder }
{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$
$\hspace{1.85cm}\text{Blau: }{\rm Pr}(3 \le z \le 5) = 0.2304+ 0.0768 + 0.0102 =1 - 0.6826 = 0.3174;$
$\hspace{1.85cm}\text{Rot: }{\rm Pr}(3 \le z \le 5) = 0.2013 + 0.0881 + 0.0264 = 0.9936 - 0.6778 = 0.3158$
(3) Es gelten weiter die Einstellungen von (1). Wie unterscheiden sich der Mittelwert $m_1$ und die Streuung $\sigma$ der beiden Binomialverteilungen?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Mittelwert:}\hspace{0.2cm}m_\text{1} = I \cdot p\hspace{0.3cm} \Rightarrow\hspace{0.3cm} m_\text{1, Blau} = 5 \cdot 0.4\underline{ = 2 =} \ m_\text{1, Rot} = 10 \cdot 0.2; $
$\hspace{1.85cm}\text{Streuung:}\hspace{0.4cm}\sigma = \sqrt{I \cdot p \cdot (1-p)} = \sqrt{m_1 \cdot (1-p)}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_{\rm Blau} = \sqrt{2 \cdot 0.6} =1.095 \le \sigma_{\rm Rot} = \sqrt{2 \cdot 0.8} = 1.265.$
(4) Setzen Sie Blau: Binomialverteilung $(I=15, p=0.3)$ und Rot: Poissonverteilung $(\lambda=4.5)$.
- Welche Unterschiede ergeben sich zwischen beiden Verteilungen hinsichtlich Mittelwert $m_1$ und Varianz $\sigma^2$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Beide Verteilungern haben gleichen Mittelwert:}\hspace{0.2cm}m_\text{1, Blau} = I \cdot p\ = 15 \cdot 0.3\underline{ = 4.5 =} \ m_\text{1, Rot} = \lambda$;
$\hspace{1.85cm} \text{Binomialverteilung: }\hspace{0.2cm} \sigma_\text{Blau}^2 = m_\text{1, Blau} \cdot (1-p)\hspace{0.15cm}\underline { = 3.15} \le \text{Poissonverteilung: }\hspace{0.2cm} \sigma_\text{Rot}^2 = \lambda\hspace{0.15cm}\underline { = 4.5}$;
(5) Es gelten die Einstellungen von (4). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(z \gt 10)$ und ${\rm Pr}(z \gt 15)$
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomial: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - {\rm Pr}(z \le 10) = 1 - 0.9993 = 0.0007;\hspace{0.3cm} {\rm Pr}(z \gt 15) = 0$.
$\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0\hspace{0.5cm}\text{Näherung: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \le {\rm Pr}(z = 16) = \lambda^{16}/16!$
Die maximale Varianz $σ^2 = I/4$ ergibt sich für die charakteristische Wahrscheinlichkeit $p = 1/2$. In diesem Fall sind die Wahrscheinlichkeit symmetrisch um den Mittelwert $m_1 = I/2 \ ⇒ \ p_μ = p_{I–μ}$.
Je mehr die charakteristische Wahrscheinlichkeit $p$ vom Wert $1/2$ abweicht,
- um so kleiner ist die Streuung $σ$, und
- um so unsymmetrischer werden die Wahrscheinlichkeiten um den Mittelwert $m_1 = I · p$.