Mobile Kommunikation/Wahrscheinlichkeitsdichte des Rayleigh–Fadings

1. Mobile Kommunikation
2. Zeitvariante Übertragungskanäle
3. Wahrscheinlichkeitsdichte des Rayleigh–Fadings

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Eine sehr allgemeine Beschreibung des Mobilfunkkanals

Im Folgenden wird zur Vereinfachung der Schreibweise auf den Zusatz „TP” verzichtet. Somit liegt das reelle Signal $s(t) = 1$ am Eingang des Mobilfunkkanals an und das Ausgangssignal $r(t)$ ist komplexwertig. Zusätzliche Rauschprozesse werden ausgeschlossen.

Das Funksignal $s(t)$ kann den Empfänger über eine Vielzahl von Pfaden erreichen, wobei die einzelnen Signalanteile in unterschiedlicher Weise gedämpft und verschieden lang verzögert werden. Allgemein kann man für das Tiefpass–Empfangssignal ohne Berücksichtigung von thermischem Rauschen schreiben:

\[r(t)= \sum_{k=1}^{K} \alpha_{k}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{k}(t)} \cdot s(t - \tau_{k}) \hspace{0.05cm}.\]

Hierbei sind folgende Bezeichnungen verwendet:

• Der zeitabhängige Dämpfungsfaktor auf dem $k$–ten Pfad ist $\alpha_k(t)$.
  

• Der zeitabhängige Phasenverlauf auf dem $k$–ten Pfad ist $\phi_k(t)$.
  

• Die zeitabhängige Laufzeit auf dem $k$–ten Pfad ist $\tau_k(t)$.
  
  

Die Anzahl $K$ der sich (zumindest geringfügig) unterscheidenden Pfade ist meist sehr groß und für eine direkte Modellierung ungeeignet. Das Modell lässt sich aber entscheidend vereinfachen, wenn man jeweils Pfade mit näherungsweise gleichen Verzögerungen zusammenfasst. Man unterscheidet somit nur noch $M$ Hauptpfade, die durch großräumige Wegeunterschiede und damit merkliche Laufzeitunterschiede gekennzeichnet sind:

\[r(t)= \sum_{m=1}^{M} \hspace{0.1cm} \sum_{n=1}^{N_m} \alpha_{m,\hspace{0.04cm}n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{m,\hspace{0.04cm}n}(t)} \cdot s(t - \tau_{m,\hspace{0.04cm}n}) \hspace{0.05cm}.\]

Die beiden bisher angegebenen Gleichungen sind identisch. Eine Vereinfachung ergibt sich erst dann, wenn man für jeden Hauptpfad $m \in \{1, \hspace{0.04cm}\text{...}\hspace{0.04cm}, M\}$ die $N_m$ Laufzeiten, die sich durch Reflexionen an Feinstrukturen sowie eventuell durch Beugungs– und Brechungserscheinungen geringfügig unterscheiden, durch eine mittlere Laufzeit ersetzt:

\[\tau_{m} = \frac{1}{N_m} \cdot \sum_{n=1}^{N_m} \tau_{m,\hspace{0.04cm}n} \hspace{0.05cm}.\]

$\text{Fazit:}$  Damit erhält man folgendes Zwischenergebnis: Das Ausgangssignal im äquivalenten Tiefpassbereich kann dargestellt werden als

\[r(t)= \sum_{m=1}^{M} z_m(t) \cdot s(t - \tau_{m}) \hspace{0.5cm} {\rm mit} \hspace{0.5cm} z_m(t) = \sum_{n=1}^{N_m} \alpha_{m,\hspace{0.04cm}n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi_{m,\hspace{0.04cm}n}(t)} \hspace{0.05cm}.\]

Frequenzselektives Fading vs. nichtfrequenzselektives Fading

Ausgehend von der soeben hergeleiteten Gleichung

\[r(t)= \sum_{m=1}^{M} z_m(t) \cdot s(t - \tau_{m}) \hspace{0.5cm} {\rm mit} \hspace{0.5cm} z_m(t) = \sum_{n=1}^{N_m} \alpha_{m,\hspace{0.04cm}n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi_{m,\hspace{0.04cm}n}(t)} \hspace{0.05cm}\]

können zwei wichtige Sonderfälle abgeleitet werden:

• Gibt es mehr als einen Hauptpfad $(M \ge 2)$, so spricht man von Mehrwegeausbreitung. Wie im Hauptkapitel Frequenzselektive Übertragungskanäle noch gezeigt werden wird, kommt es dann – je nach Frequenz – zu konstruktiven oder destruktiven Überlagerungen bis hin zu völliger Auslöschung.
• Für manche Frequenzen erweist sich die Mehrwegeausbreitung als günstig, für andere als extrem ungünstig. Man bezeichnet diesen Effekt auch als frequenzselektives Fading.
  

• Bei nur einem Hauptpfad ($(M = 1)$ vereinfacht sich die obige Gleichung wie folgt (auf den Index „$m = 1$” verzichten wir in diesem Fall) :

\[r(t)= z(t) \cdot s(t - \tau) \hspace{0.05cm}.\]

Die Verzögerung $\tau$ bewirkt hier eine für alle Frequenzen konstante Laufzeit, die nicht weiter betrachtet werden muss.

$\text{Fazit:}$  Es gibt bei dieser Konstellation keine Überlagerungen von Signalanteilen mit merklichen Laufzeitunterschieden und damit auch keine Frequenzabhängigkeit des Gesamtsignals. Man spricht deshalb von nichtfrequenzselektivem Fading oder Flat–Fading oder Rayleigh–Fading. Für dieses gilt:

\[r(t)= z(t) \cdot s(t) \hspace{0.5cm} {\rm mit} \hspace{0.5cm} z(t) = \sum_{n=1}^{N} \alpha_{n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.02cm}\cdot \hspace{0.02cm} \phi_{n}(t)} \hspace{0.05cm}. \]

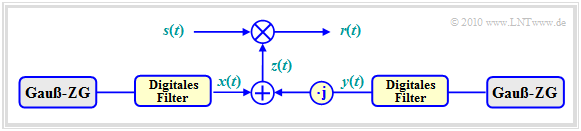
Modellierung von nichtfrequenzselektivem Fading

Rayleigh–Fading–Kanalmodell

Die Grafik zeigt das Modell zur Erzeugung von nichtfrequenzselektivem Fading   ⇒   Rayleigh–Fading.

• Das Empfangssignal $r(t)$ ergibt sich, wenn man das Sendesignal $s(t)$ mit der Zeitfunktion $z(t)$ multipliziert.
• Es sei nochmals daran erinnert, dass sich alle Signale bzw. Zeitfunktionen $s(t)$, $z(t)$ und $r(t)$ auf den äquivalenten Tiefpassbereich beziehen.

Wir betrachten die multiplikative Verfälschung $z(t)$ entsprechend diesem Rayleigh–Modell genauer. Für den komplexen Koeffizienten gilt entsprechend der letzten Seite:

\[z(t) = \sum_{n=1}^{N} \alpha_{n}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.04cm}\cdot \hspace{0.04cm} \phi_{n}(t) }= \sum_{n=1}^{N} \alpha_{n}(t) \cdot \cos\hspace{-0.1cm}\big [ \phi_{n}( t) \big ] + {\rm j}\cdot \sum_{n=1}^{N} \alpha_{n}(t) \cdot \sin\hspace{-0.1cm}\big [ \phi_{n}( t)\big ] \hspace{0.05cm}. \]

Zu dieser Gleichung und obiger Grafik ist anzumerken:

• Die zeitabhängige Dämpfung $\alpha_{n}(t)$ und die zeitabhängige Phase $\phi_{n}(t)$ hängen von den Umgebungsbedingungen ab.
• $\phi_{n}(t)$ erfasst die verschiedenen Laufzeiten auf den $N$ Pfaden und den Dopplereffekt aufgrund der Bewegung.

• Die Zeitfunktion $z(t)$ ist eine komplexe Größe, deren Real– und Imaginärteil wir im Folgenden wieder mit $x(t)$ und $y(t)$ bezeichnen.

• Eine deterministische Beschreibung der Zufallsgröße $z(t) = x(t) + {\rm j}\cdot y(t)$ ist nicht möglich, vielmehr müssen diese Funktionen durch stochastische Prozesse modelliert werden.

• Ist die Anzahl $N$ der (leicht) unterschiedlichen Laufzeiten hinreichend groß, so ergeben sich nach dem zentralen Grenzwertsatz Gaußsche Zufallsgrößen $x(t)$ und $y(t)$.

• Die beiden Komponenten $x(t)$ und $y(t)$ sind jeweils mittelwertfrei und besitzen die gleiche Varianz $\sigma^2$:

\[{\rm E}[x(t)] = {\rm E}\big[y(t)\big] = 0\hspace{0.05cm}, \hspace{0.8cm}{\rm E}\big[x^2(t)\big] = {\rm E}\big[y^2(t)\big] = \sigma^2 \hspace{0.05cm}.\]

• Zu berücksichtigen ist die Orthogonität von Realteil und Imaginärteil (jeweils Cosinus und Sinus des gleichen Arguments). Damit sind die beiden Komponenten auch unkorreliert. Nur bei Gaußschen Zufallsgrößen folgt daraus weiter die statistische Unabhängigkeit von $x(t)$ und $y(t)$.

• Aufgrund des Dopplereffekts gibt es allerdings statistische Bindungen innerhalb des Realteils $x(t)$ und innerhalb des Imaginärteils $y(t)$ . Diese beiden Größen werden im obigen Modell durch die beiden Digitalen Filter erzeugt.

Beispielhafte Signalverläufe bei Rayleigh–Fading

Die folgenden Grafiken zeigen jeweils durch Simulation gewonnene Signalverläufe von 100 ms Dauer und die dazugehörigen Dichtefunktionen. Es handelt sich um Bildschirmabzüge des Windows–Programms „Mobilfunkkanal” aus dem (ehemaligen) Praktikum Simulation digitaler Übertragungssysteme an der TU München:

• Windows–Programm MFK   ⇒   Link verweist auf die ZIP-Version des Programms und
• Praktikumsanleitung   ⇒   Link verweist auf die PDF-Version (58 Seiten).

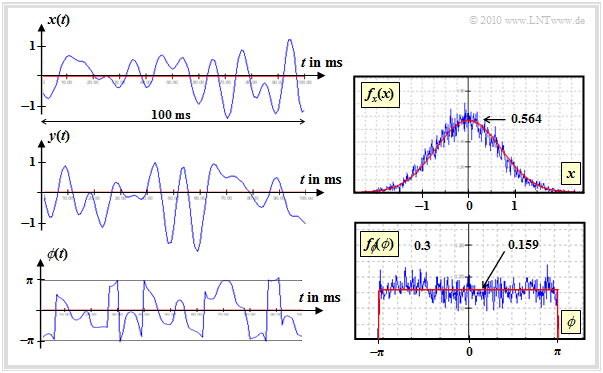
$\text{Beispiel 1:}$  Die Grafik zeigt beispielhafte Signalverläufe bei Rayleigh–Fading und die dazugehörigen Wahrscheinlichkeitsdichtefunktionen.

Realteil, Imaginärteil und Phasenverlauf bei Rayleigh-Fading

Die Darstellungen lassen sich wie folgt interpretieren:

• Der Realteil ist gaußverteilt (siehe rechte obere Grafik), wie auch aus dem Zeitsignalverlauf $x(t)$ hervorgeht. Rot eingezeichnet ist die Gaußsche WDF $f_x(x)$ und blau das durch Simulation über 10.000 Abtastwerte gewonnene Histogramm.

• Im Programm eingestellt war für diese Darstellung eine maximale Dopplerfrequenz von $f_{\rm D, \ max} = 100 \ \rm Hz$. Deshalb gibt es statistische Bindungen innerhalb der Signale $x(t)$ und $y(t)$. Genauere Angaben zum Dopplereffekt finden Sie im nächsten Kapitel.

• Die WDF $f_y(y)$ des Imaginärteils ist identisch mit $f_x(x)$. Die Varianz beträgt bei der betrachteten Konstellation jeweils $\sigma_x^2 =\sigma_y^2 = 0.5 \ (=\sigma^2)$. Zwischen $x(t)$ und $y(t)$ bestehen keine statistischen Bindungen; die Signale sind orthogonal.

• Die Phase $\phi(t)$ ist gleichverteilt zwischen $\pm\pi$. Wie aus den Sprungstellen im Phasenverlauf zu erahnen, kann $\phi(t)$ durchaus größere Werte annehmen. Alle Bereiche $(2k+1)\cdot \pi$ wurden aber bei der Histogrammerstellung auf den Wertebereich von $-\pi$ ... $+\pi$ projiziert ($k$ ganzzahlig).

• Die gleichverteilte Phase wird anhand der (hier nicht dargestellten) 2D–WDF verständlich. Diese ist rotationssymmetrisch und dementsprechend gibt es auch keine Vorzugsrichtung:

\[f_{x,\hspace{0.02cm}y}(x, y) = \frac{1}{2\pi \cdot \sigma^2} \cdot {\rm e}^{ -(x^2 + y^2)/(2\sigma^2)} .\]

Realteil, Imaginärteil, Betrag und Betragsquadrat bei Rayleigh-Fading

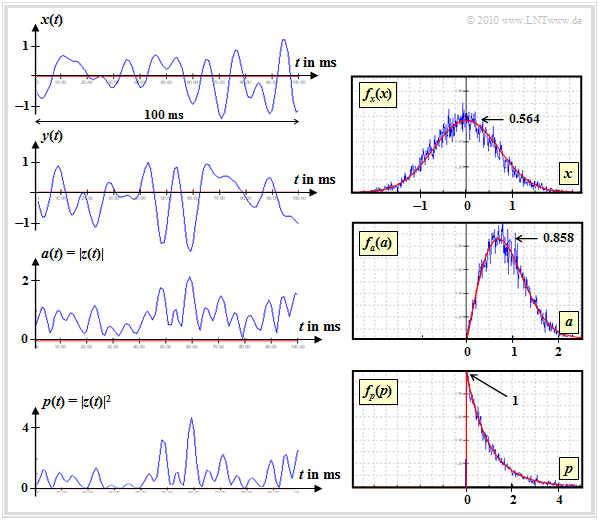
$\text{Beispiel 2:}$ Fortsetzung von $\text{Beispiel 1}$

Die nächste Grafik zeigt oben nochmals den Realteil $x(t)$ und Imaginärteil $y(t)$ von $z(t)$. Darunter gezeichnet sind Verlauf und WDF

• von Betrag $a(t) =\vert z(t)\vert$ und
• Betragsquadrat $p(t) =a^2(t) =\vert z(t)\vert^2$.
  

Aus diesen Darstellungen geht hervor:

• Der Betrag besitzt eine Rayleigh–WDF  ⇒  Name „Rayleigh–Fading”:

\[f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^{-a^2/(2\sigma^2)} \\ 0 \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.1cm} a\hspace{-0.05cm} \ge \hspace{-0.05cm}0, \\ {\rm f\ddot{u}r}\hspace{0.1cm} a \hspace{-0.05cm}<\hspace{-0.05cm} 0. \\ \end{array} \]

• Für die Momente erster bzw. zweiter Ordnung und die Varianz des Betrags $a(t) =\vert z(t)\vert $ gilt:

\[{\rm E}\big [a \big] = \sigma \cdot \sqrt {{\pi}/{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm E}\big[a^2 \big] = 2 \cdot \sigma^2\]

\[ \Rightarrow \hspace{0.3cm} {\rm Var}\big[a \big] = \sigma_a^2 = \sigma^2 \cdot \left ( 2 - {\pi}/{2}\right ) \hspace{0.05cm}. \]

• Die WDF des Betragsquadrats $p(t)$ ergibt sich durch nichtlineare Transformation der Wahrscheinlichkeitsdichtefunktion $f_a(a)$. Dies führt zu einer Exponentialverteilung:

\[f_p(p) \hspace{-0.05cm}=\hspace{-0.05cm} \left\{ \begin{array}{c} (2\sigma^2)^{-1} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm e}^{-p^2\hspace{-0.05cm}/(2\sigma^2)} \\ 0 \end{array} \right.\hspace{0.05cm} \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.05cm} p \hspace{-0.05cm}\ge \hspace{-0.05cm}0, \\ {\rm f\ddot{u}r}\hspace{0.15cm} p\hspace{-0.05cm} < \hspace{-0.05cm}0. \\ \end{array} \]

Weitere Informationen zum Rayleigh–Fading finden Sie in der Aufgabe 1.3 und der Aufgabe 1.3Z.

Aufgaben zum Kapitel

Aufgabe 1.3: Rayleigh–Fading

Aufgabe 1.3Z: Nochmals Rayleigh–Fading?