Aufgaben:Aufgabe 2.6: PN-Generator der Länge 5

• Zurück zum Buch

PN-Generator der Länge $L = 5$

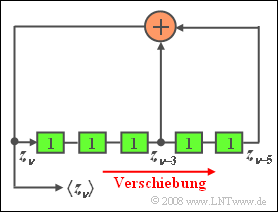
In der Grafik sehen Sie einen Pseudozufallsgenerator der Länge $L = 5$, der zur Erzeugung einer Binärfolge $\langle z_{\nu} \rangle$ eingesetzt werden soll.

• Zum Startzeitpunkt seien alle Speicherzellen mit Einsen vorbelegt.
• Zu jedem Taktzeitpunkt wird der Inhalt des Schieberegisters um eine Stelle nach rechts verschoben und der aktuell erzeugte Binärwert $z_{\nu}$ (0 oder 1) in die erste Speicherzelle eingetragen.

Hierbei ergibt sich $z_{\nu}$ aus der Modulo-2-Addition zwischen $z_{\nu-3}$ und $z_{\nu-5}$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Erzeugung von diskreten Zufallsgrößen.

• Wir verweisen hier auch auf das Lernvideo Erläuterung der PN-Generatoren an einem Beispiel.

Fragebogen

1

Wie lautet das Generatorpolynom $G(D)$ des dargestellten PN-Generators?

	$G(D) = D^5 + D^2 +1$.
	$G(D) = D^5 + D^3 +1$.
	$G(D) = D^4 + D^2 +D$.

2

Welche Oktalkennung $O_{\rm G}$ hat dieser PN-Generator?

$O_{\rm G} \ = \ $ $\ \rm (oktal)$

3

Gehen Sie davon aus, dass das Generatorpolynom $G(D)$ primitiv ist.
Ist die Ausgangsfolge $〈z_ν \rangle$ eine M-Sequenz? Wie groß ist deren Periodendauer $P$?

$P\ = \ $

4

Welche Oktalkennung $O_{\rm R}$ beschreibt das zu $G(D)$ reziproke Polynom $G_{\rm R}(D)$?

$O_{\rm R} \ = \ $ $\ \rm (oktal)$

5

Welche Aussagen gelten für die Konfiguration mit dem Polynom $G_{\rm R}(D)$?

	Es handelt sich ebenfalls um eine Folge maximaler Länge.
	Die Ausgangsfolge von $G_{\rm R}(D)$ ist die gleiche wie mit dem Generatorpolynom $G(D)$.
	Die Ausgangsfolgen von $G_{\rm R}(D)$ und $G(D)$ sind zueinander invers.
	Beide Folgen zeigen gleiche statistische Eigenschaften.
	Bei $G_{\rm R}(D)$ können alle Speicherelemente mit Nullen vorbelegt sein.

Musterlösung

Musterlösung

(1)  Richtig ist der Lösungsvorschlag 2   ⇒   $G(D) = D^5 + D^3 +1$.

• Das Generatorpolynom $G(D)$ kennzeichnet die Rückführungen, die zur Modulo-2-Addition herangezogen werden.
• $D$ ist ein formaler Parameter, der eine Verzögerung um einen Takt angibt.
• $D^3$ kennzeichnet dann eine Verzögerung um drei Takte.

(2)  Es ist $g_0 = g_3 = g_5 = 1$. alle anderen Rückführungskoeffizienten sind $0$. Daraus folgt:

$$(g_{\rm 5}\hspace{0.1cm}g_{\rm 4}\hspace{0.1cm}g_{\rm 3}\hspace{0.1cm}g_{\rm 2}\hspace{0.1cm}g_{\rm 1}\hspace{0.1cm}g_{\rm 0})=\rm (101001)_{bin}\hspace{0.15cm} \underline{=(51)_{oct}}.$$

(3)  Da das Generatorpolynom $G(D)$ primitiv ist, erhält man eine M-Sequenz. Dementsprechend ist die Periodendauer maximal:

$$P_{\rm max} = 2^{L}-1 \hspace{0.15cm}\underline {= 31}.$$

Im Theorieteil ist in der Tabelle mit den PN-Generatoren maximaler Länge (M-Sequenzen) für den Grad $5$ die Konfiguration $(51)_{\rm oct}$ aufgeführt.

(4)  Das reziproke Polynom lautet:

$$G_{\rm R}(D)=D^{\rm 5}\cdot(D^{\rm -5}+\D^{\rm -3}+ 1)= D^{\rm 5}+D^{\rm 2}+1.$$

Somit ist die Oktalkennung für diese Konfiguration $\rm (100101)_{bin}\hspace{0.15cm} \underline{=(45)_{oct}}.$

(5)  Richtig sind die Lösungsvorschläge 1, 3 und 4:

• Die Ausgangsfolge der reziproken Realisierung $G_{\rm R}(D)$ eines primitiven Polynoms $G(D)$ ist immer ebenfalls eine M-Sequenz.
• Beide Folgen sind zueinander invers. Das bedeutet:
• Die Ausgangsfolge von$(45)_{\rm oct}$ ist gleich der Folge von $(51)_{\rm oct}$, wenn man diese von rechts nach links liest und eine Phase (zyklische Verschiebung) berücksichtigt.
• Voraussetzung ist wieder, dass nicht alle Speicherzellen mit Nullen vorbelegt sind.
• Unter dieser Bedingung weisen beide Folgen tatsächlich auch gleiche statistische Eigenschaften auf.