Aufgaben:Aufgabe 4.3: Algebraische und Modulo-Summe

• Zurück zum Buch

Algebraische Summe und Modulo-2-Summe

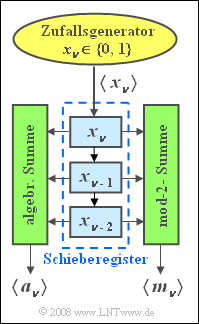
Ein „getakteter” Zufallsgenerator liefert eine Folge $\langle x_\nu \rangle$ von binären Zufallszahlen.

• Es wird nun vorausgesetzt, dass die Binärzahlen $0$ und $1$ mit gleichen Wahrscheinlichkeiten auftreten und dass die einzelnen Zufallszahlen nicht statistisch voneinander abhängen.
• Die Zufallszahlen $ x_\nu \in \{0, 1\}$ werden in die erste Speicherstelle eines Schieberegisters eingetragen und mit jeden Takt um eine Stelle nach unten verschoben.

Aus den Inhalten des dreistelligen Schieberegisters werden zwei neue Zufallsfolgen $\langle a_\nu \rangle$ und $\langle m_\nu \rangle$ gebildet. Hierbei bezeichnet:

• $a_\nu$  die algebraische Summe:

$$a_\nu=x_\nu+x_{\nu-1}+x_{\nu-2},$$

• $m_\nu$  die Modulo-2-Summe:

$$m_\nu=x_\nu\oplus x_{\nu-1}\oplus x_{\nu-2}.$$

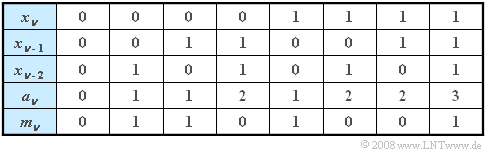
Dieser Sachverhalt ist in der nachfolgenden Tabelle nochmals dargestellt:

Tabelle zur Momentenberechnung

Hinweis:   Die Aufgabe gehört zum Kapitel Zweidimensionale Zufallsgrößen.

Fragebogen

1

Berechnen Sie die Wahrscheinlichkeiten der Zufallsgröße $m_\nu$. Wie groß ist die Wahrscheinlichkeit, dass die Modulo-2-Summe gleich $0$ ist?

${\rm Pr}(m_\nu = 0) \ = \ $

2

Bestehen statistische Abhängigkeiten innerhalb der Folge $\langle m_\nu \rangle$?

	Die Folgenelemente $m_\nu$ sind statistisch unabhängig.
	Es bestehen statistische Bindungen innerhalb der Folge $\langle m_\nu \rangle$.

3

Ermitteln Sie die Verbund-WDF $f_{xm}(x_\nu, m_\nu)$. Bewerten Sie aufgrund des Resultats die folgenden Aussagen (zutreffend oder nicht).

	Die Zufallsgrößen $x_\nu$ und $m_\nu$ sind statistisch abhängig.
	Die Zufallsgrößen $x_\nu$ und $m_\nu$ sind statistisch unabhängig.
	Die Zufallsgrößen $x_\nu$ und $m_\nu$ sind korreliert.
	Die Zufallsgrößen $x_\nu$ und $m_\nu$ sind unkorreliert.

4

Bestehen innerhalb der Folge $\langle a_\nu \rangle$ statistische Abhängigkeiten?

	Die Folgenelemente $a_\nu$ sind statistisch unabhängig.
	Es bestehen statistische Bindungen innerhalb der Folge $\langle a_\nu \rangle$.

5

Ermitteln Sie die 2D-WDF $f_{am}(a_\nu, m_\nu)$ und den Korrelationskoeffizienten $\rho_{am}$. Welche der folgenden Aussagen treffen zu?

	Die Zufallsgrößen $a_\nu$ und $m_\nu$ sind statistisch abhängig.
	Die Zufallsgrößen $a_\nu$ und $m_\nu$ sind statistisch unabhängig.
	Die Zufallsgrößen $a_\nu$ und $m_\nu$ sind korreliert.
	Die Zufallsgrößen $a_\nu$ und $m_\nu$ sind unkorreliert.

Musterlösung

Musterlösung

(1)  Aus der Tabelle auf der Angabenseite ist ersichtlich, dass bei der Modulo-2-Summe die beiden Werte $0$ und $1$ mit gleicher Wahrscheinlichkeit auftreten:   ${\rm Pr}(m_\nu = 0) = {\rm Pr}(m_\nu = 1)\hspace{0.15cm}\underline{=0.5}$

(2)  Die Tabelle zeigt, dass bei jeder Vorbelegung   ⇒   $( x_{\nu-1}, x_{\nu-2}) = (0,0), (0,1), (1,0), (1,1)$   die Werte $m_\nu = 0$ bzw. $m_\nu = 1$ mit gleicher Wahrscheinlichkeit auftreten. Anders ausgedrückt:   ${\rm Pr}(m_{\nu}\hspace{0.05cm}|\hspace{0.05cm}m_{\nu-1}) = {\rm Pr}( m_{\nu}).$ Dies entspricht genau der Definition der statistischen Unabhängigkeit.

(3)  Richtig sind der zweite und der letzte Lösungsvorschlag.

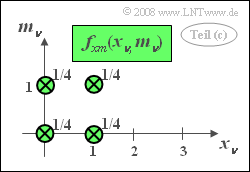
• Die 2D–WDF besteht aus vier Diracfunktionen, jeweils mit dem Gewicht $1/4$. Man erhält dieses Ergebnis beispielsweise durch Auswertung der Tabelle auf der Angabenseite.
• Da $f_{xm}(x_\nu, m_\nu)$ gleich dem Produkt $f_{x}(x_\nu) \cdot f_{m}(m_\nu)$ ist, sind die Größen $x_\nu$ und $m_\nu$ statistisch unabhängig.
• Statistisch unabhängige Zufallsgrößen sind aber natürlich auch linear statistisch unabhängig, also mit Sicherheit unkorreliert.

(4)  Innerhalb der Folge $\langle a_\nu \rangle$ der algebraischen Summe gibt es statistische Bindungen   ⇒   Vorschlag 2. Man erkennt dies daran, dass die unbedingte Wahrscheinlichkeit $ {\rm Pr}( a_{\nu} = 0) =1/8$ ist , während zum Beispiel ${\rm Pr}(a_{\nu} = 0\hspace{0.05cm}|\hspace{0.05cm}a_{\nu-1} = 3) =0$ ist.

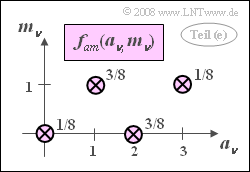
(5)  Richtig sind der erste und der letzte Lösungsvorschlag:

• Wie bei der Teilaufgabe (3) erhält man wieder vier Diracfunktionen, diesmal aber nicht mit jeweils gleichem Impulsgewicht $1/4$.
• Die zweidimensionale WDF lässt sich somit nicht als Produkt der zwei Randwahrscheinlichkeitsdichten schreiben. Das bedeutet aber, dass statistische Bindungen zwischen $a_\nu$ und $m_\nu$ bestehen müssen.
• Für den gemeinsamen Erwartungswert erhält man:

$${\rm E}[a\cdot m] = \rm \frac{1}{8}\cdot 0 \cdot 0 +\frac{3}{8}\cdot 2 \cdot 0 +\frac{3}{8}\cdot 1 \cdot 1 + \frac{1}{8}\cdot 3 \cdot 1 = \frac{3}{4}.$$

• Mit den linearen Mittelwerten ${\rm E}[a] = 1.5$ und ${\rm E}[m] = 0.5$ folgt damit für die Kovarianz:

$$\mu_{am}= {\rm E}[ a\cdot m] - {\rm E}[ a]\cdot {\rm E}[ m] = \rm 0.75-1.5\cdot 0.5 = \rm 0.$$

• Damit ist auch der Korrelationskoeffizient $\rho_{am}= 0$. Das heißt: Die vorhandenen Abhängigkeiten sind nichtlinear.
• Die Größen $a_\nu$ und $m_\nu$ sind zwar statistisch abhängig, trotzdem aber unkorreliert.