Aufgaben:Aufgabe 4.8Z: AWGN-Kanal: Unterschied zwischen den Versionen
K (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID413__Sto_Z_4_8.png|right|Modell | + | [[Datei:P_ID413__Sto_Z_4_8.png|right|frame|Modell des AWGN-Kanals]] |
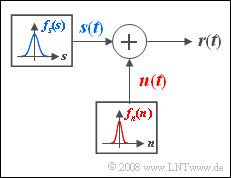
| − | Wir betrachten hier ein analoges Nachrichtensignal $s(t)$, dessen Amplitudenwerte gaußverteilt sind. Der Effektivwert $\sigma_s$ dieses mittelwertfreien Signals beträgt $1 \hspace{0.05cm} \rm V$. Diese Größe bezeichnet man auch als die ''Streuung''. | + | Wir betrachten hier ein analoges Nachrichtensignal $s(t)$, dessen Amplitudenwerte gaußverteilt sind. |
| + | *Der Effektivwert $\sigma_s$ dieses mittelwertfreien Signals beträgt $1 \hspace{0.05cm} \rm V$. | ||
| + | *Diese Größe bezeichnet man auch als die ''Streuung''. | ||
| + | |||
| + | |||
| + | Bei der Übertragung wird $s(t)$ von einem Störsignal $n(t)$ additiv überlagert, das ebenso wie $s(t)$ als gaußverteilt und mittelwertfrei angenommen werden kann. | ||
| + | *Der Effektivwert (die Streuung) des Störsignals sei allgemein $\sigma_n$. | ||
| + | *Es kann angenommen werden, dass zwischen Nutzsignal $s(t)$ und Störsignal $n(t)$ keine statistischen Abhängigkeiten bestehen. | ||
| − | |||
Man bezeichnet eine solche Konstellation als <i>Additive White Gaussian Noise</i> (AWGN) und verwendet als Qualitätskriterium für das Empfangssignal $r(t)$ das Signal-zu-Stör-Leistungsverhältnis (''Signal-to-Noise-Ratio''): | Man bezeichnet eine solche Konstellation als <i>Additive White Gaussian Noise</i> (AWGN) und verwendet als Qualitätskriterium für das Empfangssignal $r(t)$ das Signal-zu-Stör-Leistungsverhältnis (''Signal-to-Noise-Ratio''): | ||
:$${\rm SNR} = {\sigma_s^2}/{\sigma_n^2}.$$ | :$${\rm SNR} = {\sigma_s^2}/{\sigma_n^2}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| Zeile 15: | Zeile 25: | ||
*Bezug genommen wird auch auf das Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen|Zweidimensionale Gaußsche Zufallsgrößen]]. | *Bezug genommen wird auch auf das Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen|Zweidimensionale Gaußsche Zufallsgrößen]]. | ||
| + | |||
| Zeile 20: | Zeile 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie die WDF $f_r(r)$ des Empfangssignals $r(t)$ allgemein an. Wie groß ist der Effektivwert $\sigma_r$, wenn $\sigma_n =0.75 \hspace{0.05cm} \rm V$ beträgt? | + | {Geben Sie die WDF $f_r(r)$ des Empfangssignals $r(t)$ allgemein an. <br>Wie groß ist der Effektivwert $\sigma_r$, wenn $\sigma_n =0.75 \hspace{0.05cm} \rm V$ beträgt? |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_r \ = $ { 1.25 3% } $ \ \rm V$ | + | $\sigma_r \ = \ $ { 1.25 3% } $ \ \rm V$ |
| − | {Berechnen Sie den Korrelationskoeffizienten $\rho_{sr}$, der zwischen den beiden Signalen $s(t)$ | + | {Berechnen Sie den Korrelationskoeffizienten $\rho_{sr}$, der zwischen den beiden Signalen $s(t)$ und $r(t)$ besteht. <br>Welcher Wert ergibt sich für $\sigma_n =0.75 \hspace{0.05cm} \rm V$? |
|type="{}"} | |type="{}"} | ||
| − | $\rho_{sr} \ = $ { 0.8 3% } | + | $\rho_{sr} \ = \ $ { 0.8 3% } |
| Zeile 33: | Zeile 44: | ||
<br>Welcher Koeffizient ergibt sich für $10 \cdot {\rm lg \ SNR = 30 \ dB}$? | <br>Welcher Koeffizient ergibt sich für $10 \cdot {\rm lg \ SNR = 30 \ dB}$? | ||
|type="{}"} | |type="{}"} | ||
| − | + | $\rho_{sr} \ = \ $ { 0.9995 0.1% } | |
Version vom 17. August 2018, 12:02 Uhr
Wir betrachten hier ein analoges Nachrichtensignal $s(t)$, dessen Amplitudenwerte gaußverteilt sind.
- Der Effektivwert $\sigma_s$ dieses mittelwertfreien Signals beträgt $1 \hspace{0.05cm} \rm V$.
- Diese Größe bezeichnet man auch als die Streuung.
Bei der Übertragung wird $s(t)$ von einem Störsignal $n(t)$ additiv überlagert, das ebenso wie $s(t)$ als gaußverteilt und mittelwertfrei angenommen werden kann.
- Der Effektivwert (die Streuung) des Störsignals sei allgemein $\sigma_n$.
- Es kann angenommen werden, dass zwischen Nutzsignal $s(t)$ und Störsignal $n(t)$ keine statistischen Abhängigkeiten bestehen.
Man bezeichnet eine solche Konstellation als Additive White Gaussian Noise (AWGN) und verwendet als Qualitätskriterium für das Empfangssignal $r(t)$ das Signal-zu-Stör-Leistungsverhältnis (Signal-to-Noise-Ratio):
- $${\rm SNR} = {\sigma_s^2}/{\sigma_n^2}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Linearkombinationen von Zufallsgrößen.
- Bezug genommen wird auch auf das Kapitel Zweidimensionale Gaußsche Zufallsgrößen.
Fragebogen
Musterlösung
- $$f_r(r)= \frac {1}{\sqrt{2 \pi} \cdot \sigma_r} \cdot {\rm e}^{-r^2/(2 \sigma_r^2)}.$$
Die Varianzen von $s(t)$ und $n(t)$ addieren sich. Deshalb erhält man mit $\sigma_s =1 \hspace{0.05cm} \rm V$ und $\sigma_n =0.75 \hspace{0.05cm} \rm V$:
- $$\sigma_r = \sqrt{\sigma_s^2 + \sigma_n^2} =\sqrt{{(\rm 1\hspace{0.1cm}V)^2} + {(\rm 0.75\hspace{0.1cm}V)^2}}\hspace{0.15cm}\underline{ = {\rm 1.25\hspace{0.1cm}V}}.$$
(2) Für den Korrelationskoeffizienten gilt mit dem gemeinsamen Moment $m_{sr}$:
- $$\rho_{sr } = \frac{m_{sr }}{\sigma_s \cdot \sigma_r}.$$
Hierbei ist berücksichtigt, dass $s(t)$ und auch $r(t)$ mittelwertfrei sind, so dass $\mu_{sr} =m_{sr}$ gilt. Da $s(t)$ und $n(t)$ als statistisch unabhängig voneinander und damit als unkorreliert vorausgesetzt wurden, gilt weiter:
- $$m_{sr} = {\rm E}[s(t) \cdot r(t)] = {\rm E}[s^2(t)] + {\rm E}[s(t) \cdot n(t)] ={\rm E}[s^2(t)] = \sigma_s^2.$$
- $$\rightarrow \hspace{0.5cm} \rho_{sr } = \frac{\sigma_s}{ \sigma_r} = \sqrt{\frac{\sigma_s^2}{\sigma_s^2 + \sigma_n^2}} = \left (1+ {\sigma_n^2}/{\sigma_s^2}\right)^{-1/2}.$$
Mit $\sigma_s =1 \hspace{0.05cm} \rm V$, $\sigma_n =0.75 \hspace{0.05cm} \rm V$ und $\sigma_r =1.25 \hspace{0.05cm} \rm V$ erhält man $\rho_{sr }\hspace{0.15cm}\underline{ = 0.8}$.
(3) Der in der letzten Teilaufgabe berechnete Ausdruck kann mit der Abkürzung ${\rm SNR} =\sigma_s^2/\sigma_n^2$ wie folgt dargestellt werden:
- $$\rho_{sr } = \rm \frac{1}{ \sqrt{1 + \frac{1}{SNR}}} \approx \frac{1}{ {1 + \frac{1}{2 \cdot SNR}}} \approx 1 - \frac{1}{2 \cdot SNR}.$$
Der Signal-zu-Stör-Abstand $10 \cdot {\rm lg \ SNR = 30 \ dB}$ führt zum absoluten Wert $\rm SNR = 1000$. In die obige Gleichung eingesetzt ergibt dies näherungsweise einen Korrelationskoeffizienten von $\rho_{sr }\hspace{0.15cm}\underline{ = 0.9995}$.