Aufgaben:Aufgabe 4.13Z: AMI-Code

• Zurück zum Buch

AKF bei AMI-Codierung

Zur Spektralanpassung (Formung) eines Digitalsignals an die Eigenschaften des Kanals verwendet man so genannte Pseudoternärcodes. Bei diesen Codes wird die binäre Quellensymbolfolge $\langle q_\nu \rangle$ nach einer festen Vorschrift in eine Folge $\langle c_\nu \rangle$ von Ternärsymbolen umgesetzt:

$$q_{\nu} \in \{ -1,\hspace{0.1cm} +1 \} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} c_{\nu} \in \{ -1, \hspace{0.1cm}0, \hspace{0.1cm}+1 \} .$$

Der bekannteste Vertreter dieser Codeklasse ist der AMI-Code (von Alternate Mark Inversion). Hier wird

• der Binärwert $q_\nu = -1$ stets auf $c_\nu = 0$ abgebildet,
• während $q_\nu = +1$ abwechselnd (alternierend) durch die Ternärwerte $c_\nu = +1$ und $c_\nu = -1$ dargestellt wird.

Vereinbarungsgemäß soll beim ersten Auftreten von $q_\nu = +1$ das Ternärsymbol $c_\nu = +1$ ausgewählt werden.

Weiter wird vorausgesetzt, dass

• die zwei möglichen Quellensymbole jeweils gleichwahrscheinlich sind und
• die Quellensymbolfolge $\langle q_\nu \rangle$ keine inneren statistischen Bindungen aufweist.

Somit sind alle diskreten AKF-Werte gleich Null mit Ausnahme von $\varphi_q(k=0)$:

$$\varphi_q ( k \cdot T) = 0 \hspace{0.5cm} {\rm f alls} \hspace{0.5cm} k \not= 0.$$

Hierbei bezeichnet $T$ den Abstand der Quellen– bzw. Codesymbole. Verwenden Sie den Wert $T = 1 \hspace{0.05cm} \rm µ s$.

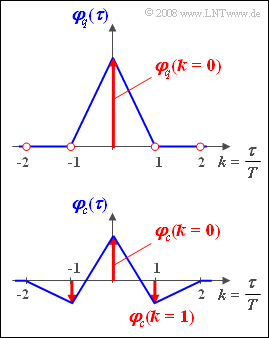
Das Bild zeigt die gegebenen Autokorrelationsfunktionen. Bitte beachten Sie:

• Rot eingezeichnet sind jeweils die zeitdiskreten Darstellungen ${\rm A} \{ \varphi_q(\tau) \}$ und ${\rm A} \{ \varphi_c(\tau) \}$ der Autokorrelationsfunktionen, jeweils mit dem Bezugswert $T$ .
• Die blau dargestellten Funktionen zeigen die zeitkontinuierlichen Verläufe $\varphi_q(\tau)$ und $\varphi_c(\tau)$ der AKF, wobei Rechtecksignale vorausgesetzt sind.

Hinweise:

• Die Aufgabe gehört zum Kapitel Leistungsdichtespektrum.
• Bezug genommen wird auch auf das Kapitel Autokorrelationsfunktion sowie auf die Seite Numerische_LDS-Ermittlung.

• Benutzen Sie die folgende Fourierkorrespondenz, wobei ${\rm \Delta} (t)$ einen um $t = 0$ symmetrischen Dreieckimpuls mit ${\rm \Delta} (t= 0) = 1$ und ${\rm \Delta} (t) = 0$ für $|t| \ge T$ bezeichnet:

$${\rm \Delta} (t) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} T \cdot {\rm si}^2 ( \pi f T).$$

Fragebogen

1

Wie groß ist der diskrete AKF–Wert der Quellensymbole für $k = 0$?

$\varphi_q(k=0) \ = \ $

2

Welche Aussagen gelten für die LDS–Funktionen ${\it \Phi}_q(f)$ und ${\rm P} \{ {\it \Phi}_q(f) \}$?

	${\rm P} \{ {\it \Phi}_q(f) \}$ ist für alle Frequenzen eine Konstante.
	${\it \Phi}_q(f)$ ist für $|f \cdot T| < 0.5$ konstant und außerhalb $0$.
	${\it \Phi}_q(f)$ verläuft $\rm si^2$-förmig.

3

Die Quellensymbolfolge sei $\langle q_\nu \rangle = \langle +1, -1, +1, +1, -1, +1, +1, -1, -1, -1 \rangle$.
Wie lauten die Codesymbole $c_\nu$? Geben Sie das Codesymbol $c_6$ ein.

$c_6 \ = \ $

4

Wie groß ist der diskrete AKF–Wert der Codesymbole für $k = 0$.

$\varphi_c(k=0) \ = \ $

5

Berechnen Sie die AKF-Werte $\varphi_c(k=+1)$ und $\varphi_c(k=-1)$.

$\varphi_c(k=+1) \ = \ $

$\varphi_c(k=-1) \ = \ $

6

Welche spektrale Leistungsdichte ${\it \Phi}_c(f)$ ergibt sich für die Frequenz $f=0$ bzw. für $f = 500 \hspace{0.08cm} \rm kHz$.   Hinweis:   Für $|k| \ge 2$ sind alle AKF–Werte $\varphi_c(k) \equiv 0$.

${\it \Phi}_c(f = 0) \ = \ $ $\ \cdot 10^{-6} \ \rm 1/Hz$

${\it \Phi}_c(f = 500 \hspace{0.08cm} \rm kHz)\ = \ $ $\ \cdot 10^{-6} \ \rm 1/Hz$

Musterlösung

Musterlösung

(1)  Der diskrete AKF-Wert für $k = 0$ gibt den quadratischen Mittelwert (hier gleich der Varianz) der Quellensymbole an.

• Da $q_\nu$ nur die Werte $-1$ und $+1$ annehmen kann, ist $\varphi_q(k=0)\hspace{0.15cm}\underline{= 1}$.

(2)  Richtig sind die Lösungsvorschläge 1 und 3:

• Die zeitdiskrete AKF und deren Fouriertransformierte lauten:

$${\rm A} \{ \varphi_q ( \tau ) \} = \varphi_q ( k = 0) \cdot T \cdot \delta (\tau) \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{\it \Phi_q}( f) \} = \varphi_q ( k = 0) \cdot T = T.$$

• Es ist berücksichtigt, dass $\varphi_q(k=0)= \sigma_q^2= 1$ ist. Das bedeutet:  

Die periodische Fortsetzung von ${\rm P} \{ {\it \Phi}_q(f) \}$ ergibt somit für alle Frequenzen den gleichen Wert.

• Dagegen kann die zeitkontinuierliche AKF wie folgt dargestellt werden:  

$$ \varphi_q ( \tau ) = {\rm A} \{ \varphi_q ( \tau ) \} \star ( {\rm \Delta} ( \tau) / T ).$$

• Das dazugehörige Leistungsdichtespektrum (Fouriertransformierte der AKF) ist dann das Produkt der Fouriertransformierten der beiden Faltungsterme:  

$$ {\it \Phi_q} ( f) = {\rm P} \{ {\it \Phi_q}( f) \} \cdot {\rm si}^2 (\pi f T ) = T \cdot {\rm si}^2 (\pi f T ) .$$

• Aufgrund der gewählten AKF-Interpolation (mit Geradenabschnitten) aus ihren Abtastwerten ergibt sich ein si²-förmiges LDS.
• Ein rechteckförmiges Spektrum gemäß Lösungsvorschlag (2) würde sich nur bei si-förmiger Interpolation einstellen.

(3)  Die codierte Folge lautet:   $\langle +1, 0, -1, +1, 0, -1, +1, 0, 0, 0 \rangle$.

Das 6. Symbol ist somit $c_6\hspace{0.15cm}\underline{= -1}$.

(4)  Die Auftrittswahrscheinlichkeiten der Werte $-1$, $\ 0$ und $+1$ sind $0.25, 0.5, 0.25$. Daraus folgt:

$$\varphi_c ( k = 0) = 0.25 \cdot (-1)^2 + 0.5 \cdot 0^2 +0.25 \cdot (+1)^2\hspace{0.15cm}\underline{ = 0.5}. $$

(5)  Für den AKF-Wert bei $k = 1$ betrachtet man das Produkt $c_{\nu} \cdot c_{\nu+1}$.

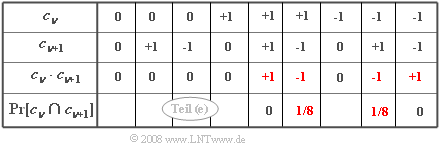
• Es ergeben sich die rechts gezeigten Kombinationen.
• Einen Beitrag liefern nur Produkte $c_{\nu} \cdot c_{\nu+1} \ne 0$ mit ${\rm Pr}\big[c_{\nu} \cdot c_{\nu+1}\big] \ne 0$:

$$\varphi_c ( k = 1) = {\rm Pr} \big [( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \big ] \cdot (+1) \cdot (-1) + {\rm Pr} \big [ ( c_{\nu} = -1) \cap ( c_{\nu + 1} = +1) \big ] \cdot (-1) \cdot (+1).$$

Zur AKF-Berechnung des AMI-Codes

In der Tabelle sind diese Terme rot gekennzeichnet. Weiter gilt:

$$ {\rm Pr} \big [ ( c_{\nu} = +1) \cap ( c_{\nu + 1} = -1) \big ] = $$

$$ = {\rm Pr} ( c_{\nu} = +1) \cdot {\rm Pr} \left ( c_{\nu + 1} = -1 | c_{\nu } = +1) \right ) = \frac{1}{4} \cdot \frac{1}{2}= \frac{1}{8} . $$

Hierbei ist vorausgesetzt, dass $+1$ mit der Wahrscheinlichkeit $0.25$ auftritt und danach $-1$ nur in der Hälfte der Fälle folgt.

Das gleiche Ergebnis erhält man für den zweiten Beitrag. Damit gilt:

$$\varphi_c ( k = 1) = \frac {1}{8} \cdot (+1)\cdot (-1) + \frac {1}{8} \cdot (-1)\cdot (+1) \hspace{0.15cm}\underline{= -0.25}.$$

$$\varphi_c ( k = -1) = \varphi_c ( k = 1) \hspace{0.15cm}\underline{= -0.25}.$$

Zur Berechnung von $\varphi_c ( k = 2)$ muss über $3^3 = 27$ Kombinationen gemittelt werden. Das Ergebnis ist jedoch Null.

(6)  Die Fouriertransformierte der zeitdiskreten AKF ${\rm A} \{ \varphi_c(\tau) \}$ lautet:

$$P \{{\it \Phi_c}( f) \} = T\cdot \varphi_c ( k = 0) +2T \cdot \varphi_c ( k = 1) \cdot {\rm cos} ( 2 \pi f T ).$$

• Mit dem Ergebnis der letzten Teilaufgabe folgt daraus:

$$P \{{\it \Phi}_c( f) \} = \frac {T}{2} (1 - {\rm cos} ( 2 \pi f T ) )= T \cdot {\rm sin}^2 ( \pi f T ).$$

• Wie unter Punkt (2) gezeigt, gilt dann für das LDS – also die Fouriertransformierte von $\varphi_c(\tau)$:

$${\it \Phi_c}( f) = T \cdot {\rm sin}^2 ( \pi f T ) \cdot {\rm si}^2 ( \pi f T ) = T \cdot \frac {{\rm sin}^4 ( \pi f T )}{( \pi f T )^2 } .$$

$$\Rightarrow \hspace{0.3cm} {\it \Phi_c}( f = 0) \hspace{0.15cm}\underline{= 0}, \hspace{0.8cm} {\it \Phi_c}( f = {\rm500 \hspace{0.1cm}kHz}) = T \cdot \frac {{\rm sin}^4 ( \pi /2 )}{( \pi /2 )^2 } = \frac {4 T}{\pi^2} \rm \hspace{0.15cm}\underline{= 0.405 \cdot 10^{-6} \ {1}/{Hz}}.$$