Aufgaben:Aufgabe 1.4Z: Entropie der AMI-Codierung

• Zurück zum Buch

Binäres Quellensignal (oben) und ternäres Codersignal (unten)

Wir gehen von ähnlichen Voraussetzungen wie in der Aufgabe 1.4 aus:   Eine Binärquelle liefert die Quellensybolfolge $\langle q_\nu \rangle$ mit $q_\nu \in \{ {\rm L}, {\rm H} \}$, wobei es keine statistischen Bindungen zwischen den einzelnen Folgenelementen gibt.

Für die Symbolwahrscheinlichkeiten gelte:

• $p_{\rm L} =p_{\rm H} = 1/2$ (in den Teilaufgaben 1 und 2),
• $p_{\rm L} = 1/4, \, p_{\rm H} = 3/4$ (Teilaufgaben 3, 4 und 5),
• $p_{\rm L} = 3/4, \, p_{\rm H} = 1/4$ (Teilaufgabe 6).

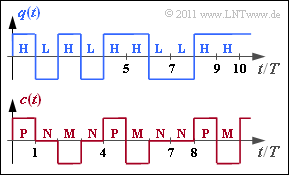
Das dargestellte Codersignal $c(t)$ und die zugehörige Symbolfolge $\langle c_\nu \rangle$ mit $c_\nu \in \{{\rm P}, {\rm N}, {\rm M} \}$ ergibt sich aus der AMI–Codierung (Alternate Mark Inversion) nach folgender Vorschrift:

• Das Binärsymbol $\rm L$  ⇒  Low wird stets durch das Ternärsymbol $\rm N$  ⇒  Null dargestellt.
• Das Binärsymbol $\rm H$  ⇒  High wird ebenfalls deterministisch, aber alternierend (daher der Name „AMI”) durch die Symbole $\rm P$  ⇒  Plus und $\rm M$  ⇒  Minus codiert.

In dieser Aufgabe sollen für die drei oben genannten Parametersätze der Entscheidungsgehalt $H_0$ sowie die resultierende Entropie $H_{\rm C}$ der Codesymbolfolge $\langle c_\nu \rangle$ bestimmt werden. Die relative Redundanz der Codefolge ergibt sich daraus entsprechend der Gleichung

$$r_{\rm C} = \frac{H_{\rm 0}-H_{\rm C}}{H_{\rm C}} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Nachrichtenquellen mit Gedächtnis.
• Bezug genommen wird insbesondere auf die Seite Die Entropie des AMI–Codes.

• Allgemein bestehen folgende Relationen zwischen dem Entscheidungsgehalt $H_0$, der Entropie $H$ (hier gleich $H_{\rm C}$) und den Entropienäherungen:

$$H \le \ \text{...} \ \le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$

• In Aufgabe 1.4 wurden für gleichwahrscheinliche Symbole $\rm L$ und $\rm H$ die Entropie–Näherungen wie folgt berechnet (jeweils in „bit/Symbol”):

$$H_1 = 1.500\hspace{0.05cm},\hspace{0.2cm} H_2 = 1.375\hspace{0.05cm},\hspace{0.2cm}H_3 = 1.292 \hspace{0.05cm}.$$

Fragebogen

1

Die Quellensymbole seien gleichwahrscheinlich $(p_{\rm L} = p_{\rm H}= 1/2)$. Wie groß ist die Entropie $H_{\rm C}$ der Codesymbolfolge $\langle c_\nu \rangle$?

$H_{\rm C} \ = \ $ $\ \rm bit/Ternärsymbol$

2

Wie groß ist die relative Redundanz der Codesymbolfolge?

$r_{\rm C} \ = \ $ $\ \rm \%$

3

Für die Binärquelle gelte nun $p_{\rm L} = 1/4$  und  $p_{\rm H} = 3/4$. Welcher Wert ergibt sich nun für die Entropie der Codesymbolfolge?

$H_{\rm C} \ = \ $ $\ \rm bit/Ternärsymbol$

4

Wie groß ist nun die relative Redundanz der Codesymbolfolge?

$r_{\rm C} \ = \ $ $\ \rm \%$

5

Berechnen Sie die Näherung $H_{\rm 1}$ der Coderentropie für $p_{\rm L} = 1/4$  und  $p_{\rm H} = 3/4$.

$H_{\rm 1} \ = \ $ $\ \rm bit/Ternärsymbol$

6

Berechnen Sie die Näherung $H_{\rm 1}$ der Coderentropie für $p_{\rm L} = 3/4$  und  $p_{\rm H} = 1/4$.

$H_{\rm 1} \ = \ $ $\ \rm bit/Ternärsymbol$

Musterlösung

Musterlösung

(1)  Da durch den AMI–Code weder neue Information hinzukommt noch Information verschwindet, ist die Entropie $H_{\rm C}$ der Codesymbolfolge $\langle c_\nu \rangle$ gleich der Quellenentropie $H_{\rm Q}$. Bei gleichwahrscheinlichen und statistisch voneinander unabhängigen Quellensymbolen gilt deshalb:

$$H_{\rm Q} {= 1 \,{\rm bit/Bin\ddot{a}rsymbol}} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_{\rm C} \hspace{0.15cm} \underline {= 1 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

(2)  Der Entscheidungsgehalt einer ternären Quelle beträgt $H_0 = \log_2 \; (3) = 1.585\; \rm bit/Symbol$. Damit ergibt sich für die relative Redundanz

$$r_{\rm C} =1 -{H_{\rm C}/H_{\rm 0}}=1-1/{\rm log}_2\hspace{0.05cm}(3) \hspace{0.15cm} \underline {= 36.9 \,\%} \hspace{0.05cm}.$$

(3)  Es gilt weiter $H_{\rm C} = H_{\rm Q}$. Wegen den ungleichen Symbolwahrscheinlichkeiten ist aber nun $H_{\rm Q}$ kleiner:

$$H_{\rm Q} = \frac{1}{4} \cdot {\rm log}_2\hspace{0.05cm} (4) + \frac{3}{4} \cdot {\rm log}_2\hspace{0.1cm} (4/3) {= 0.811 \,{\rm bit/Bin\ddot{a}rsymbol}} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_{\rm C} = H_{\rm Q} \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

(4)  In Analogie zur Teilaufgabe (2) gilt nun $r_{\rm C} = 1 - 0.811/1.585 \hspace{0.15cm} \underline {= 48.8 \,\%} \hspace{0.05cm}.$ Man kann dieses Ergebnis verallgemeinern. Es gilt nämlich:

$$(1-0.488) = (1- 0.189) \cdot (1- 0.369)\hspace{0.3cm} \Rightarrow\hspace{0.3cm} (1-r_{\rm Codefolge}) = (1-r_{\rm Quelle}) \cdot (1- r_{\rm AMI-Code}) \hspace{0.05cm}.$$

(5)  Da jedes $\rm L$ auf $\rm N$ abgebildet wird und $\rm H$ alternierend auf $\rm M$ und $\rm P$, gilt

$$p_{\rm N} = p_{\rm L} = 1/4\hspace{0.05cm},\hspace{0.2cm}p_{\rm P} = p_{\rm M} = p_{\rm H}/2 = 3/8\hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_1 = {1}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4) + 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8/3) \hspace{0.15cm} \underline {= 1.56 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

(6)  Nun ergeben sich die Auftrittswahrscheinlichkeiten der Ternärsymbole zu $p_{\rm N} = 3/4$ sowie $p_{\rm P} = p_{\rm M} =1/8$. Somit gilt:

$$H_1 = {3}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4/3) + 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} \underline {= 1.06 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

Interpretation:

• Für $p_{\rm L} = 1/4, \ p_{\rm H} = 3/4$ ergibt sich $H_1 = 1.56 \; \rm bit/Symbol$.
• Für $p_{\rm L} = 3/4, \ p_{\rm H} = 1/4$ ergibt sich dagegen mit $H_1 = 1.06 \; \rm bit/Symbol$ ein deutlich kleinerer Wert.
• Für beide Parameterkombinationen gilt aber gleichermaßen:

$$H_0 = 1.585 \,{\rm bit/Symbol}\hspace{0.05cm},\hspace{0.2cm}H_{\rm C} = \lim_{k \rightarrow \infty } H_k = 0.811 \,{\rm bit/Symbol} \hspace{0.05cm}.$$

Daraus folgt:
Betrachtet man zwei Nachrichtenquellen $\rm Q1$ und $\rm Q2$ mit gleichem Symbolumfang $M$   ⇒   Entscheidungsgehalt  $H_0 = \rm const.$, wobei bei der Quelle $\rm Q1$ die Entropienäherung erster Ordnung $(H_1)$ deutlich größer ist als bei der Quelle $\rm Q2$, so kann man daraus noch lange nicht schließen, dass die Entropie von $\rm Q1$ tatsächlich größer ist als die Entropie von $\rm Q2$. Vielmehr muss man für beide Quellen

• genügend viele Entropienäherungen $H_1$, $H_2$, $H_3$, ... berechnen, und
• daraus (grafisch oder analytisch) den Grenzwert von $H_k$ für $k \to \infty$ bestimmen.

Erst dann ist eine endgültige Aussage über die Entropieverhältnisse möglich.