Aufgaben:Aufgabe 1.4Z: Komplexes Nyquistspektrum: Unterschied zwischen den Versionen
| Zeile 100: | Zeile 100: | ||
Hz}\hspace{0.1cm}\underline { = 1\,{\rm V}}\hspace{0.05cm}.$$ | Hz}\hspace{0.1cm}\underline { = 1\,{\rm V}}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' Beim Nyquistimpuls treten die äquidistanten Nulldurchgänge im Abstand $T = 1/(2f_{\rm Nyq}) = 100 \, \rm | + | '''(4)''' Beim Nyquistimpuls treten die äquidistanten Nulldurchgänge im Abstand $T = 1/(2f_{\rm Nyq}) = 100 \, \rm µ s$ auf. Daraus erhält man direkt: |
| − | :$$g(t= 100\,{\rm | + | :$$g(t= 100\,{\rm µ s}) = \ \hspace{0.1cm}\underline { g(T) = 0,}$$ |
| − | :$$g(t= 200\,{\rm | + | :$$g(t= 200\,{\rm µ s}) = \ \hspace{0.1cm}\underline {g(2T) = 0} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Dieses Ergebnis folgt auch aus der angegebenen Gleichung mit $r = 0.4$: | Dieses Ergebnis folgt auch aus der angegebenen Gleichung mit $r = 0.4$: | ||
| Zeile 111: | Zeile 111: | ||
| − | '''(5)''' Entsprechend der unter (4) angegebenen Gleichung gilt: | + | '''(5)''' Entsprechend der unter '''(4)''' angegebenen Gleichung gilt: |
| − | :$$g(t= 250\,{\rm | + | :$$g(t= 250\,{\rm µ s})= g_0 \cdot {\rm si} ( {2.5 \cdot \pi |
})\cdot {\rm si} ( \pi )\hspace{0.1cm}\underline { = 0} \hspace{0.05cm}.$$ | })\cdot {\rm si} ( \pi )\hspace{0.1cm}\underline { = 0} \hspace{0.05cm}.$$ | ||
Diese Nullstelle ist auf den zweiten Term zurückzuführen und liegt nicht im Nyquist–Zeitraster $\nu T$ | Diese Nullstelle ist auf den zweiten Term zurückzuführen und liegt nicht im Nyquist–Zeitraster $\nu T$ | ||
| − | '''(6)''' Für die folgende Herleitung gelte $g(t)= g_{\rm R}(t) + g_{\rm I}(t) \hspace{0.05cm},$ wobei $g_{\rm R}(t)$ auf den Realteil und $g_{\rm I}(t)$ auf den Imaginärteil von $G(f)$ zurückgeht. Der erste Anteil ist dabei genau wie unter Punkt (4) berechnet: | + | '''(6)''' Für die folgende Herleitung gelte $g(t)= g_{\rm R}(t) + g_{\rm I}(t) \hspace{0.05cm},$ wobei $g_{\rm R}(t)$ auf den Realteil und $g_{\rm I}(t)$ auf den Imaginärteil von $G(f)$ zurückgeht. |
| + | *Der erste Anteil ist dabei genau wie unter Punkt '''(4)''' berechnet: | ||
:$$g_{\rm R} ( t )= g_0 \cdot {\rm si} \left ( {\pi \cdot | :$$g_{\rm R} ( t )= g_0 \cdot {\rm si} \left ( {\pi \cdot | ||
t}/{T}\right)\cdot {\rm si} \left ( {\pi \cdot 0.4 \cdot | t}/{T}\right)\cdot {\rm si} \left ( {\pi \cdot 0.4 \cdot | ||
t}/{T}\right) \hspace{0.05cm}.$$ | t}/{T}\right) \hspace{0.05cm}.$$ | ||
| − | Zur Erfüllung des ersten Nyquistkriteriums muss für den Imaginärteil mit $1/T = 10 \, \rm kHz$ gelten: | + | *Zur Erfüllung des ersten Nyquistkriteriums muss für den Imaginärteil mit $1/T = 10 \, \rm kHz$ gelten: |
:$$\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G \left ( f - | :$$\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G \left ( f - | ||
{k}/{T} \right)\right]= 0 \hspace{0.05cm}.$$ | {k}/{T} \right)\right]= 0 \hspace{0.05cm}.$$ | ||
| − | *Mit den gegebenen Eckfrequenzen $f_{1} = 3 \, \rm kHz$ und $f_{2} = 7 \ \rm kHz$ liegen die beiden Dreiecke um $\pm 5\, \rm kHz$, so dass obige Gleichung erfüllt ist. Gleiches gilt für $f_{1} = 4.5\, \rm kHz$ und $f_{2} = 5.5 \, \rm kHz$. | + | *Mit den gegebenen Eckfrequenzen $f_{1} = 3 \, \rm kHz$ und $f_{2} = 7 \ \rm kHz$ liegen die beiden Dreiecke um $\pm 5\, \rm kHz$, so dass obige Gleichung erfüllt ist. |
| − | *Dagegen liegen die Dreieckspitzen mit $f_{1} = 3\, \rm kHz$ und $f_{2} = 5 \, \rm kHz$ bei $\pm 4 \ \rm kHz$. In diesem Fall löschen sich die Dreieckfunktionen durch die periodische Fortsetzung nicht aus und die Nyquistbedingung ist nicht erfüllt. | + | *Gleiches gilt für $f_{1} = 4.5\, \rm kHz$ und $f_{2} = 5.5 \, \rm kHz$. |
| + | *Dagegen liegen die Dreieckspitzen mit $f_{1} = 3\, \rm kHz$ und $f_{2} = 5 \, \rm kHz$ bei $\pm 4 \ \rm kHz$. | ||
| + | *In diesem Fall löschen sich die Dreieckfunktionen durch die periodische Fortsetzung nicht aus und die Nyquistbedingung ist nicht erfüllt. | ||
| + | |||
Richtig sind somit die <u>Lösungsvorschläge 1 und 3</u>. | Richtig sind somit die <u>Lösungsvorschläge 1 und 3</u>. | ||
| − | '''(7)''' Mit dem Ergebnis $g_{\rm R}(2.5T) = 0$ aus (3) folgt $g(2.5T) = g_{\rm I}(2.5T)$, wobei $g_{\rm I}(t)$ die Fourierrücktransformierte von ${\rm j}\cdot \ G_{\rm I}(f)$ ist. Es gilt: | + | '''(7)''' Mit dem Ergebnis $g_{\rm R}(2.5T) = 0$ aus '''(3)''' folgt $g(2.5T) = g_{\rm I}(2.5T)$, wobei $g_{\rm I}(t)$ die Fourierrücktransformierte von ${\rm j}\cdot \ G_{\rm I}(f)$ ist. Es gilt: |
:$${\rm j} \cdot G_{\rm I}(f) = {\rm j} \cdot\left[ \delta(f + f_{\rm Nyq}) - \delta(f - f_{\rm Nyq})\right] \star D(f) \hspace{0.3cm} | :$${\rm j} \cdot G_{\rm I}(f) = {\rm j} \cdot\left[ \delta(f + f_{\rm Nyq}) - \delta(f - f_{\rm Nyq})\right] \star D(f) \hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} g_{\rm I}(t) = 2 \cdot {\rm sin} ( 2 | \Rightarrow \hspace{0.3cm} g_{\rm I}(t) = 2 \cdot {\rm sin} ( 2 | ||
\pi\cdot f_{\rm Nyq} \cdot t )\cdot d(t)\hspace{0.05cm}.$$ | \pi\cdot f_{\rm Nyq} \cdot t )\cdot d(t)\hspace{0.05cm}.$$ | ||
| − | Die Sinusfunktion erzwingt die erforderlichen Nulldurchgänge bei Vielfachen von $T = 100 \, \rm | + | *Die Sinusfunktion erzwingt die erforderlichen Nulldurchgänge bei Vielfachen von $T = 100 \, \rm µ s$. |
| + | *$D(f)$ ist eine Dreieckfunktion um $f = 0$ mit $D(f = 0) = B$ und der einseitigen Breite $f_{0}= f_{2} – f_{\rm Nyq} = f_{\rm Nyq} – f_{1} = 2 \, \rm kHz$. | ||
| + | *Für die dazugehörige Zeitfunktion kann somit entsprechend der Angabe geschrieben werden: | ||
:$$g_{\rm I}(t ) = 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2 | :$$g_{\rm I}(t ) = 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2 | ||
\pi\cdot f_{\rm Nyq} \cdot t)\cdot {\rm si}^2(\pi\cdot f_{\rm 0} \cdot t) \hspace{0.05cm}.$$ | \pi\cdot f_{\rm Nyq} \cdot t)\cdot {\rm si}^2(\pi\cdot f_{\rm 0} \cdot t) \hspace{0.05cm}.$$ | ||
| − | Insbesondere gilt für den Zeitpunkt $t = 250 \, \rm | + | *Insbesondere gilt für den Zeitpunkt $t = 250 \, \rm µ s$ (grünes Quadrat): |
:$$g(t = 2.5 T) = g_{\rm I}(t = 2.5 T) = \ 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2.5 | :$$g(t = 2.5 T) = g_{\rm I}(t = 2.5 T) = \ 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2.5 | ||
\pi )\cdot {\rm si}^2(\frac{\pi}{2}) = \ \frac{8}{\pi^2} \cdot 10^{-4 }\,\frac{\rm V}{\rm Hz}\cdot 2 \cdot 10^{3} \,{\rm | \pi )\cdot {\rm si}^2(\frac{\pi}{2}) = \ \frac{8}{\pi^2} \cdot 10^{-4 }\,\frac{\rm V}{\rm Hz}\cdot 2 \cdot 10^{3} \,{\rm | ||
Hz}\hspace{0.1cm}\underline {= 0.162\,{\rm | Hz}\hspace{0.1cm}\underline {= 0.162\,{\rm | ||
V}} \hspace{0.05cm}.$$ | V}} \hspace{0.05cm}.$$ | ||
| + | |||
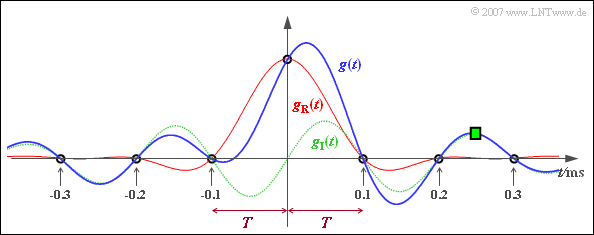
[[Datei:P_ID1283__Dig_Z_1_4g.png|right|frame|Unsymmetrischer Nyquistimpuls]] | [[Datei:P_ID1283__Dig_Z_1_4g.png|right|frame|Unsymmetrischer Nyquistimpuls]] | ||
Die Grafik zeigt die Veränderung der Zeitfunktion aufgrund des Imaginärteils (grüner Zeitverlauf): | Die Grafik zeigt die Veränderung der Zeitfunktion aufgrund des Imaginärteils (grüner Zeitverlauf): | ||
Version vom 30. Januar 2019, 17:47 Uhr
Betrachtet wird ein Impuls $g(t)$ mit Spektrum $G(f)$ gemäß der Skizze. Man erkennt aus dieser Darstellung:
- Der Realteil von $G(f)$ ist trapezförmig mit den Eckfrequenzen $f_{1} = 3 \, \rm kHz$ und $f_{2} = 7 \, \rm kHz$. Im Bereich $|f| < f_{1}$ gilt:
- $${\rm Re}\big[G(f)\big] = A = 10^{-4} \, \rm V/Hz.$$
- Der Imaginärteil von $G(f)$ wird für die Teilaufgaben (1) bis (5) stets zu ${\rm Im}\big[G(f)\big] =0$ angenommen.
In diesem Fall ist $g(t)$ sicher ein Nyquistimpuls. - Ab der Teilaufgabe (6) hat der Imaginärteil ${\rm Im}[G(f)]$ im Bereich $f_{1} \leq | f | \leq f_{2}$ einen Dreiecksverlauf mit den Werten $\pm B$ bei den Dreieckspitzen.
Zu prüfen ist, ob der Impuls $g(t)$ auch mit komplexem Spektrum der ersten Nyquistbedingung genügt:
- $$g(\nu T) = \left\{ \begin{array}{c} g_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} \nu = 0 \hspace{0.05cm}, \\ \nu \ne 0 \hspace{0.1cm}. \\ \end{array}$$
Im Verlauf dieser Aufgabe wird auf folgende Beschreibungsgrößen Bezug genommen:
- Die Nyquistfrequenz gibt den Symmetriepunkt des Flankenabfalls an:
- $$f_{\rm Nyq}= \frac{1}{2T}= \frac{f_1 +f_2 } {2 }\hspace{0.05cm}.$$
- Der Rolloff–Faktor ist ein Maß für die Flankensteilheit:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Eigenschaften von Nyquistsystemen.
- Als bekannt vorausgesetzt werden kann die Fourierrücktransformierte $g(t)$ eines trapezförmigen Nyquistspektrums mit Rolloff–Faktor $r$:
- $$g ( t )= g_0 \cdot {\rm si} \left ( {\pi \cdot t}/{T}\right)\cdot {\rm si} \left ( {\pi \cdot r \cdot t}/{T}\right).$$
- Ein dreieckförmiges Tiefpass–Spektrum $G(f)$, das auf $| f | < f_{0}$ begrenzt ist und bei dem $G(f = 0) = B$ gilt, führt nach Fourierrücktransformation zur Zeitfunktion
- $$g ( t )= B \cdot f_0 \cdot {\rm si}^2 \left ( {\pi f_0 t}\right)\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- $$f_{\rm Nyq}= \frac{f_1 +f_2 } {2 }= \frac{3\, {\rm kHz} + 7\, {\rm kHz}} {2 } \hspace{0.1cm}\underline { = 5\, {\rm kHz}} \hspace{0.05cm}.$$
(2) Der Rolloff–Faktor ist ebenfalls durch die beiden Eckfrequenzen $f_{1}$ und $f_{2}$ festgelegt:
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } = \frac{7\, {\rm kHz} - 3\, {\rm kHz}} {7\, {\rm kHz} + 3\, {\rm kHz} }\hspace{0.1cm}\underline { = 0.4 }\hspace{0.05cm}.$$
(3) Bei einem Impuls mit reellem Tiefpass–Spektrum liegt das Maximum stets bei $t = 0$ und es gilt:
- $$g_0 = g(t=0) = \int_{-\infty}^{+\infty}G(f) \,{\rm d} f = A \cdot 2 f_{\rm Nyq} = 10^{-4 }\,\frac{\rm V}{\rm Hz}\cdot 2 \cdot 5 \cdot10^{3} \,{\rm Hz}\hspace{0.1cm}\underline { = 1\,{\rm V}}\hspace{0.05cm}.$$
(4) Beim Nyquistimpuls treten die äquidistanten Nulldurchgänge im Abstand $T = 1/(2f_{\rm Nyq}) = 100 \, \rm µ s$ auf. Daraus erhält man direkt:
- $$g(t= 100\,{\rm µ s}) = \ \hspace{0.1cm}\underline { g(T) = 0,}$$
- $$g(t= 200\,{\rm µ s}) = \ \hspace{0.1cm}\underline {g(2T) = 0} \hspace{0.05cm}.$$
Dieses Ergebnis folgt auch aus der angegebenen Gleichung mit $r = 0.4$:
- $$g ( t )= g_0 \cdot {\rm si} \left ( {\pi \cdot t}/{T}\right)\cdot {\rm si} \left ( {\pi \cdot 0.4 \cdot t}/{T}\right) \hspace{0.05cm}.$$
Verantwortlich dafür, dass die erste Nyquistbedingung erfüllt wird, ist der erste Term.
(5) Entsprechend der unter (4) angegebenen Gleichung gilt:
- $$g(t= 250\,{\rm µ s})= g_0 \cdot {\rm si} ( {2.5 \cdot \pi })\cdot {\rm si} ( \pi )\hspace{0.1cm}\underline { = 0} \hspace{0.05cm}.$$
Diese Nullstelle ist auf den zweiten Term zurückzuführen und liegt nicht im Nyquist–Zeitraster $\nu T$
(6) Für die folgende Herleitung gelte $g(t)= g_{\rm R}(t) + g_{\rm I}(t) \hspace{0.05cm},$ wobei $g_{\rm R}(t)$ auf den Realteil und $g_{\rm I}(t)$ auf den Imaginärteil von $G(f)$ zurückgeht.
- Der erste Anteil ist dabei genau wie unter Punkt (4) berechnet:
- $$g_{\rm R} ( t )= g_0 \cdot {\rm si} \left ( {\pi \cdot t}/{T}\right)\cdot {\rm si} \left ( {\pi \cdot 0.4 \cdot t}/{T}\right) \hspace{0.05cm}.$$
- Zur Erfüllung des ersten Nyquistkriteriums muss für den Imaginärteil mit $1/T = 10 \, \rm kHz$ gelten:
- $$\sum_{k = -\infty}^{+\infty} {\rm Im}\left[G \left ( f - {k}/{T} \right)\right]= 0 \hspace{0.05cm}.$$
- Mit den gegebenen Eckfrequenzen $f_{1} = 3 \, \rm kHz$ und $f_{2} = 7 \ \rm kHz$ liegen die beiden Dreiecke um $\pm 5\, \rm kHz$, so dass obige Gleichung erfüllt ist.
- Gleiches gilt für $f_{1} = 4.5\, \rm kHz$ und $f_{2} = 5.5 \, \rm kHz$.
- Dagegen liegen die Dreieckspitzen mit $f_{1} = 3\, \rm kHz$ und $f_{2} = 5 \, \rm kHz$ bei $\pm 4 \ \rm kHz$.
- In diesem Fall löschen sich die Dreieckfunktionen durch die periodische Fortsetzung nicht aus und die Nyquistbedingung ist nicht erfüllt.
Richtig sind somit die Lösungsvorschläge 1 und 3.
(7) Mit dem Ergebnis $g_{\rm R}(2.5T) = 0$ aus (3) folgt $g(2.5T) = g_{\rm I}(2.5T)$, wobei $g_{\rm I}(t)$ die Fourierrücktransformierte von ${\rm j}\cdot \ G_{\rm I}(f)$ ist. Es gilt:
- $${\rm j} \cdot G_{\rm I}(f) = {\rm j} \cdot\left[ \delta(f + f_{\rm Nyq}) - \delta(f - f_{\rm Nyq})\right] \star D(f) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} g_{\rm I}(t) = 2 \cdot {\rm sin} ( 2 \pi\cdot f_{\rm Nyq} \cdot t )\cdot d(t)\hspace{0.05cm}.$$
- Die Sinusfunktion erzwingt die erforderlichen Nulldurchgänge bei Vielfachen von $T = 100 \, \rm µ s$.
- $D(f)$ ist eine Dreieckfunktion um $f = 0$ mit $D(f = 0) = B$ und der einseitigen Breite $f_{0}= f_{2} – f_{\rm Nyq} = f_{\rm Nyq} – f_{1} = 2 \, \rm kHz$.
- Für die dazugehörige Zeitfunktion kann somit entsprechend der Angabe geschrieben werden:
- $$g_{\rm I}(t ) = 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2 \pi\cdot f_{\rm Nyq} \cdot t)\cdot {\rm si}^2(\pi\cdot f_{\rm 0} \cdot t) \hspace{0.05cm}.$$
- Insbesondere gilt für den Zeitpunkt $t = 250 \, \rm µ s$ (grünes Quadrat):
- $$g(t = 2.5 T) = g_{\rm I}(t = 2.5 T) = \ 2 \cdot B \cdot f_0 \cdot{\rm sin} ( 2.5 \pi )\cdot {\rm si}^2(\frac{\pi}{2}) = \ \frac{8}{\pi^2} \cdot 10^{-4 }\,\frac{\rm V}{\rm Hz}\cdot 2 \cdot 10^{3} \,{\rm Hz}\hspace{0.1cm}\underline {= 0.162\,{\rm V}} \hspace{0.05cm}.$$
Die Grafik zeigt die Veränderung der Zeitfunktion aufgrund des Imaginärteils (grüner Zeitverlauf):
- Es ergibt sich nun ein unsymmetrischer Funktionsverlauf $g(t)$, der blau dargestellt ist.
- Die Nulldurchgänge von $g_{\rm R}(t)$ im Abstand $T$ bleiben jedoch erhalten.