Aufgaben:Aufgabe 4.17: Nichtkohärentes On-Off-Keying

• Zurück zum Buch

Rayleigh– und Riceverteilung

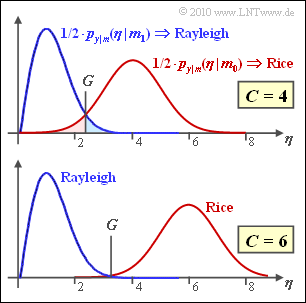
Die Abbildung zeigt die beiden Dichtefunktionen, die sich bei einer nichtkohärenten Demodulation von On–Off–Keying  (OOK) ergeben. Dabei wird vorausgesetzt, dass die zwei OOK–Signalraumpunkte bei  $\boldsymbol{s}_0 = C$  $($Nachricht  $m_0)$  und bei $\boldsymbol{s}_1 = 0$  $($Nachricht  $m_1)$  liegen.

Die Symbolfehlerwahrscheinlichkeit dieses Systems wird durch die folgende Gleichung beschrieben:

$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot \int_{0}^{G} p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} | \hspace{0.05cm}m_0) \,{\rm d} \eta +{1}/{ 2} \cdot \int_{G}^{\infty} p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} |\hspace{0.05cm} m_1) \,{\rm d} \eta \hspace{0.05cm}.$$

Mit der Streuung  $\sigma_n = 1$, die im Folgenden vorausgesetzt wird, lautet die sich für  $m = m_1$  ergebende Rayleighverteilung (blaue Kurve):

$$p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} \hspace{0.05cm}| m_1) = \eta \cdot {\rm e }^{-\eta^2/2} \hspace{0.05cm}.$$

Die Riceverteilung (rote Kurve) kann man im vorliegenden Fall $($wegen  $C\gg \sigma_n)$  durch eine Gaußkurve annähern:

$$p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm} |\hspace{0.05cm} m_0) = \frac{1}{\sqrt{2\pi}} \cdot {\rm e }^{-(\eta-C)^2/2} \hspace{0.05cm}.$$

Die optimale Entscheidergrenze  $G_{\rm opt}$  ergibt sich aus dem Schnittpunkt von roter und blauer Kurve.

• Aus den beiden Skizzen erkennt man, dass  $G_{\rm opt}$  von  $C$  abhängt.
• Für die obere Grafik gilt  $C = 4$, für die untere  $C = 6$.
• Alle Größen sind normiert und es wird stets  $\sigma_n = 1$  vorausgesetzt.

Hinweise:

• Die Aufgabe gehört zum Themengebiet des Kapitels  Trägerfrequenzsysteme mit nichtkohärenter Demodulation.
• Für das komplementäre Gaußsche Fehlerintegral können Sie folgende Näherungen verwenden:

$${\rm Q }(1.5) \approx 0.0668\hspace{0.05cm}, \hspace{0.5cm}{\rm Q }(2.5) \approx 0.0062\hspace{0.05cm}, \hspace{0.5cm} {\rm Q }(2.65) \approx 0.0040 \hspace{0.05cm}.$$

• Sie können Ihre Ergebnisse mit dem interaktiven Applet  Nichtkohärentes On–Off–Keying  überprüfen.

Fragebogen

1

Welcher Zusammenhang besteht zwischen der mittleren Symbolenergie  $E_{\rm S}$  und der Konstanten  $C$  der Riceverteilung?

	$E_{\rm S} = C$,
	$E_{\rm S} = C^2$,
	$E_{\rm S} = C^2/2$.

2

Welche Bestimmungsgleichung gilt für die optimale Entscheidergrenze  $G_{\rm opt}$?

	$G = C/2$,
	$G \, –1/C \cdot {\rm ln} \, (G) = C/2 + 1/(2C) \cdot {\rm ln} \, (2\pi)$,
	$G \, –1/C \cdot {\rm ln} \, (G)$.

3

Bestimmen Sie die optimale Entscheidergrenze für  $C = 4$.

$G_{\rm opt} \ = \ $

4

Welche Symbolfehlerwahrscheinlichkeit ergibt sich für  $C = 4$  und  $G = 2.5 \approx G_{\rm opt}$?

$p_{\rm S} \ = \ $ $\ \% $

5

Bestimmen Sie die optimale Entscheiderschwelle für  $C = 6$.

$G_{\rm opt} \ = \ $

6

Welche Symbolfehlerwahrscheinlichkeit ergibt sich mit  $C = 6$  und  $G = 3.5\approx G_{\rm opt}$?

$p_{\rm S} \ = \ $ $\ \% $

Musterlösung

Musterlösung

(1)  Richtig istder Lösungsvorschlag 3:

• Die Energie ist gleich dem Wert $\boldsymbol{s}_0 = C$ in der Signalraumkonstellation zum Quadrat, geteilt durch $2$.
• Der Faktor $1/2$ berücksichtigt hierbei, dass die Nachricht $m_1$ keinen Energiebeitrag liefert ($\boldsymbol{s}_1 = 0$).

(2)  Richtig ist hier der Lösungsvorschlag 2:

• Die optimale Entscheidergrenze $G$ liegt beim Schnittpunkt der beiden dargestellten Kurven.
• Der Faktor $1/2$ berücksichtigt die gleichwahrscheinlichen Nachrichten $m_0$ und $m_1$. Damit erhält man folgende Bestimmungsgleichung:

$${G}/{2} \cdot {\rm exp } \left [ - {G^2 }/{2 }\right ] = \frac{1}{2 \cdot \sqrt{2\pi}} \cdot {\rm exp } \left [ - \frac{G^2 - 2 C \cdot G + C^2}{2 }\right ]$$

$$\Rightarrow \hspace{0.3cm} \sqrt{2\pi} \cdot G = {\rm exp } \left [ C \cdot G - C^2/2 \right ] \hspace{0.3cm}\Rightarrow \hspace{0.3cm} C \cdot G - {\rm ln }\hspace{0.15cm} (\sqrt{2\pi} \cdot G) - C^2/2 = 0$$

$$\Rightarrow \hspace{0.3cm} G - {1}/{C} \cdot {\rm ln }\hspace{0.15cm} ( G) = C/2 + {1}/({2C}) \cdot {\rm ln }\hspace{0.15cm} (\sqrt{2\pi}) = C/2 + {1}/({2C}) \cdot {\rm ln }\hspace{0.15cm} ({2\pi})\hspace{0.05cm}.$$

(3)  Mit $C = 4$ lautet die unter (2) angegebene Bestimmungsgleichung

$$f(G) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} G - {1}/{C} \cdot {\rm ln }\hspace{0.15cm} ( G) - C/2 - {1}/({2C}) \cdot {\rm ln }\hspace{0.15cm} ({2\pi})= G - 0.25 \cdot {\rm ln }\hspace{0.15cm} ( G) - 2 - {\rm ln }\hspace{0.15cm} ({2\pi})/8 \approx G - 0.25 \cdot {\rm ln }\hspace{0.15cm} ( G) - 2.23 = 0 \hspace{0.05cm}.$$

• Diese Gleichung kann nur numerisch gelöst werden:

$$G = 2.0\text{:}\hspace{0.15cm}f(G) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.403 \hspace{0.05cm}, \hspace{0.2cm}G = 3.0\text{:}\hspace{0.15cm}f(G) = 0.495 \hspace{0.05cm}, \hspace{0.2cm}G = 2.5\text{:}\hspace{0.15cm}f(G) = 0.041\hspace{0.05cm},$$

$$ G = 2.4\text{:}\hspace{0.15cm}f(G) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.049 \hspace{0.05cm}, \hspace{0.2cm}G = 2.46\text{:}\hspace{0.15cm}f(G) \approx 0 \hspace{0.05cm}.$$

• Die optimale Entscheidergrenze liegt demnach bei $G_{\rm opt} \underline {= 2.46 \approx 2.5}$.

(4)  Die Fehlerwahrscheinlichkeit setzt sich aus zwei Anteilen zusammen:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot {\rm Pr}({\cal{E}}\hspace{0.05cm}| \hspace{0.05cm} m = m_1)+{1}/{ 2}\cdot {\rm Pr}({\cal{E}}\hspace{0.05cm}| \hspace{0.05cm} m = m_0)\hspace{0.05cm}.$$

• Der erste Anteil (Verfälschung von $m_1$ nach $m_0$) ergibt sich aus der Überschreitung der Grenze $G$ durch die Rayleighverteilung

$${\rm Pr}({\cal{E}} \hspace{0.05cm}| \hspace{0.05cm} m = m_1) = \int_{G}^{\infty} p_{y\hspace{0.05cm}| \hspace{0.05cm}m} (\eta \hspace{0.05cm}| \hspace{0.05cm} m_1) \,{\rm d} \eta = {\rm e }^{-G^2/2}= {\rm e }^{-3.125}\approx 0.044 \hspace{0.05cm}.$$

• Der zweite Anteil (Verfälschung von $m_0$ nach $m_1$) ergibt sich aus der Riceverteilung, die hier durch die Gaußverteilung angenähert ist:

$${\rm Pr}({\cal{E}}| m = m_0) = \int_{0}^{G} p_{y\hspace{0.05cm}| \hspace{0.05cm}m} (\eta \hspace{0.05cm}| \hspace{0.05cm} m_0) \,{\rm d} \eta = \frac{1}{\sqrt{2\pi}} \cdot \int_{0}^{G} {\rm e }^{-(\eta-C)^2/2} \,{\rm d} \eta \hspace{0.05cm}.$$

• Dieser Anteil lässt sich mit dem komplementären Gaußschen Fehlerintegral ${\rm Q}(x)$ angeben:

$${\rm Pr}({\cal{E}}\hspace{0.05cm}| \hspace{0.05cm} m = m_0) = {\rm Pr}(y < G-C) = {\rm Pr}(y > C-G) = {\rm Q }(\frac{C-G}{\sigma_n})= {\rm Q }(\frac{4-2.5}{1})= {\rm Q }(1.5) \approx 0.0688 \hspace{0.05cm}. $$

• Damit erhält man insgesamt:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot 0.0440 +{1}/{ 2} \cdot 0.0668 \approx \underline{5.54\, \%}\hspace{0.05cm}.$$

Hinweis:   Eine Systemsimulation hat ergeben, dass sich eine etwas kleinere Fehlerwahrscheinlichkeit ergibt, wenn man anstelle der Gaußnäherung die tatsächliche Riceverteilung ansetzt. Dann gilt mit $G = 2.5$:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot 0.0440 + {1}/{ 2} \cdot 0.0484 \approx \underline{4.62\, \%}\hspace{0.05cm}.$$

Die Gaußnäherung liefert also eine obere Schranke für die tatsächliche Fehlerwahrscheinlichkeit.

(5)  Mit  $C = 6$  lautet die unter (3) angegebene Bestimmungsgleichung

$$f(G)= G - {1}/{C} \cdot {\rm ln }\hspace{0.15cm} ( G) - C/2 - \frac{1}{2C} \cdot {\rm ln }\hspace{0.15cm} ({2\pi}) \approx G - {\rm ln }\hspace{0.15cm} ( G)/6 - 3.153 = 0 \hspace{0.05cm},$$

$$G = 3.0\hspace{-0.1cm}:\hspace{0.15cm}f(G) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.336 \hspace{0.05cm}, \hspace{0.2cm}G = 3.50\hspace{-0.1cm}:\hspace{0.15cm}f(G) = 0.138 \hspace{0.05cm},$$

$$ G = 3.3\hspace{-0.1cm}:\hspace{0.15cm}f(G) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.052 \hspace{0.05cm}, \hspace{0.2cm}G = 3.35\hspace{-0.1cm}:\hspace{0.15cm}f(G) \approx 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{G_{\rm opt} \approx 3.35}\hspace{0.05cm}.$$

(6)  Analog zur Teilaufgabe (4) erhält man mit $G = 3.5$:

$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot {\rm e }^{-G^2/2} +{1}/{ 2} \cdot {\rm Q }(C-G)= {1}/{ 2} \cdot {\rm e }^{-6.125} + {1}/{ 2} \cdot {\rm Q }(2.5)= {1}/{ 2} \cdot 2.2 \cdot 10^{-3} + {1}/{ 2} \cdot 6.2 \cdot 10^{-3} \underline{= 0.42 \,\%} \hspace{0.05cm}.$$

• Für  $C = 6$  ergibt sich mit der hierfür optimalen Entscheidergrenze ($G_{\rm opt} = 3.35$) eine etwa um den Faktor $10$ kleinere Fehlerwahrscheinlichkeit als mit $C = 4$:

$$p_{\rm S} = {1}/{ 2} \cdot {\rm e }^{-5.61} + {1}/{ 2} \cdot {\rm Q }(2.65)= {1}/{ 2} \cdot 3.6 \cdot 10^{-3} +{1}/{ 2} \cdot 4 \cdot 10^{-3}= {0.38 \,\%} \hspace{0.05cm}.$$

• Die tatsächliche Fehlerwahrscheinlichkeit bei Verwendung der Riceverteilung (keine Gaußnäherung) liefert einen etwas kleineren Wert:   $0.33\%$.